8. Стохастические дифференциальные уравнения 80

8. Стохастические дифференциальные уравнения (все проверить!)

Уравнение ФПК (7.21) было получено для марковских процессов первого порядка. Однако многие задачи статистической радиофизики описываются дифференциальными уравнениями более высокого порядка. Часто для их решения достаточно свести уравнения, описывающие исследуемую систему, к первому порядку, используя, например, метод медленно меняющихся амплитуд. Другой вариант – введение векторной n-мерной случайной функции, для которой марковский процесс будет процессом первого порядка. В этом случае можно использовать многомерное уравнение ФПК вида (7.21), а набор начальных условий принимает вид.

Следует заметить, что применение уравнения ФПК к решению реальных физических задач не всегда возможно, поскольку часто неизвестна связь коэффициентов сноса A(t,x) и диффузииB(t,x) с параметрами исследуемой системы.

В п. 5 мы уже рассматривали уравнение, описывающее линейную систему, вида

,

(8.1)

где и– дифференциальные операторы,f(t) – входное воздействие,x(t) – реакция системы. В рамках статистической радиофизики можно считать, что уравнение (8.1) записано для реализацииx(t) случайного процесса(t), причем причины случайного характера уравнения (8.1) могут быть различными – случайными могут быть либо входное воздействиеf(t), либо начальные условия уравнения, либо дифференциальные операторыи. В любом случае уравнение (8.1) являетсястохастическим дифференциальным уравнением.

Если известно аналитическое решение уравнения (8.1), его можно усреднить и получить, например, среднее и автокорреляционную функцию процесса. Однако это возможно далеко не всегда. Специфика стохастических дифференциальных уравнений состоит в том, что даже если неизвестно аналитическое решение, на основе уравнения (8.1) составить и решить уравнения для средних или автокорреляционных функций. Для реализации такого подхода необходимо выяснить, при каких условиях процесс на выходе системы можно считать марковским и как связать коэффициенты сноса A(t,x) и диффузииB(t,x) уравнения ФПК с параметрами операторови. Для ответа на эти вопросы рассмотрим еще один класс случайных функций.

1. Случайные функции с независимыми приращениями

Рассмотрим класс функций, приращения которых на неперекрывающихся временных интервалах являются независимыми случайными величинами. Разобьем интервал [0, t] наnинтерваловt_i=t_i+1–t_i, причемt₀= 0,t_n=t. Тогда случайный процесс(t) можно представить в виде

,

(8.2)

где _i=(t_i+1) –(t_i) – независимые случайные величины, а его дисперсия равна

.

(8.3)

Если функция (t) непрерывна почти наверняка и ее приращения на сколь угодно малых интервалахt_iнезависимы, то, переходя в выражениях (8.2) и (8.3) к пределу приn, в силу центральной предельной теоремы для величины(t) =(t) –(0) получим нормальную функцию распределения

,

(8.4)

где

.

(8.5)

Если рассматриваемый процесс (t) стационарен и имеет нулевое среднее, на основе выражения (8.2) можно записать

.

(8.6)

Единственным неотрицательным решением функционального уравнения (8.5) является линейно зависящая от времени функция вида

.

(8.7)

Таким образом, однородная непрерывная случайная функция с независимыми приращениями распределена нормально (8.4) с дисперсией, пропорциональной времени (8.6), то есть – соответствует диффузионному уравнению (7.18).

Рассмотрим производную стационарной случайной функции (t) с независимыми приращениями и выделим в ней линейный по времени множитель

.

В соответствии с выражением (8.6), дисперсия функции (t) равна

,

что возможно только в случае, если ’(t) –-коррелированный процесс, то есть

.
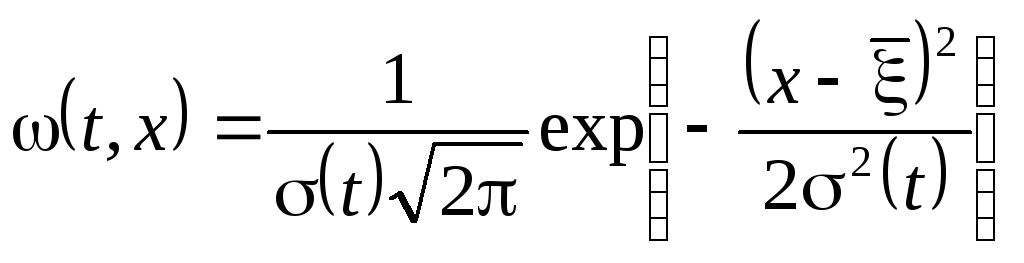