Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КузминАМ Основы теории критичности 2008

.pdf

Скачиваний:

193

Добавлен:

16.08.2013

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 169 10 11 12 13 14 15 16 > Следующая >>>

В этом выражении ψ0 (r ) – собственная функция задачи (1.7), соответствующая числу α02

(r ) + α2ψ

(r ) = 0 ,

(3.56)

а амплитуды I0(k ) – решения уравнений:

k−1

( k )

−α02 D(k ) I0( k ) − Σ(adk ) I0(k ) + ∑Σ(dj→k ) I0( j) +

∑ν (fl )Σ(fl ) I0(l ) = 0 ,

Кэф

j=1

l=1

k =1, 2,…, m .

(3.57)

Поскольку равенства (3.57) образуют систему линейных однородных уравнений, то значения I0(k ) могут быть определены

лишь с точностью до постоянного множителя. Удобно его выбрать так, чтобы:

1	m	(l )	(l )
	(l )
	∑l=1 ν f	Σf	I0	=1.	(3.58)
Кэф

k−1

χ(k ) + ∑Σ(dj→k ) I0( j )

Тогда	I (k ) =			j=1			,	k =1,2,…, m ,		(3.59)
		α02 D( k ) +Σ(adk )
	0
что позволяет без			итераций рассчитать I0(k ) последовательно,
начиная с I0(1) . После этого нетрудно с помощью равенства (3.58)
найти Кэф . Если окажется,					что значение Кэф ≠1, то необходимо
изменить свойства реактора, пересчитать амплитуды										I0(k ) и вновь
проверить выполнение условия (3.58).
	Значения	I0(k )		дают	представление о спектре					нейтронов
f (k ) (k =1,2,…, m)			в	реакторе. Подразумевая под						величиной
f (k ) (r )	отношение		f (k ) (r ) =			φ(k ) (r )			, получим, что в реакторе
						m
						∑φ(k ) (r )
						k=1

без отражателя спектр нейтронов не зависит от пространственных координат r .

3.5.Двухгрупповой метод для многозонного реактора

Вслучае многозонного реактора аналитическое решение задачи

окритичности существует лишь в одномерной геометрии. Хотя оно может быть получено при произвольном числе энергетических групп, в дальнейшем ограничимся 2-групповым приближением и реактором на тепловых нейтронах. Будем считать (как и в разделе 3.1), что все замедляющиеся (быстрые) нейтроны включены в 1-ю группу, тепловые – во 2-ю группу, а асимптотические

распределения потоков φ(1) (r ), φ( 2) (r ) находятся, решая

уравнения (3.45) и рассчитывая макроскопические сечения по формулам (3.46), (3.47).

ˆ	= − λ , гдеλ – константа,
Введем в рассмотрение оператор Lλ

а– оператор Лапласа, определенный на множестве функций

Ω, непрерывных вместе с частными производными 2-го порядка.

Действие такого оператора на функцию Сψ (r ) ( С–

произвольный множитель, не зависящий от переменных r ) заключается в следующем:

Lλ (Cψ ) = C ψ (r ) −λCψ (r ) .

(3.60)

Тогда уравнения (3.45) для любой зоны реактора с постоянными свойствами можно записать в виде (индекс зоны пока опускаем):

(2)

−

φ(1) (r ) = −

φ( 2)

(r ) ,

∞

(3.61)

D(1)

Σ(1)

−

φ( 2)

(r ) = −

(2d)

φ(1) (r ) ,

(3.62)

∞

ν (1)f Σ(1)f

где τ =

∞

ε =

Σ(1)

− μ

. В

1 +ε

Kэф

Кэф

ξΣs

дальнейшем считаем, что квадрат длины диффузии тепловых нейтронов L2 ≠τ .

Подействуем на обе части уравнения (3.61) оператором
−	1
		. Учитывая равенство (3.62) , получим:
	2	. Учитывая равенство (3.62) , получим:
	L

(1)

K∞ −1−ε

(1)

(

(r )) −

(r )

−

(r ) = 0 .

(3.63)

L τc

К такому же виду приводится уравнение для функции φ(2) (r ) ,

если

на

обе части

равенства (3.62)

подействовать

оператором

−

что общие решения для

(1)

(r )

. Это говорит о том,

φ(2) (r )

строятся на

базе

одних

и тех же

частных

решений.

качестве таких решений можно взять функции ψ (r ) Ω , не равные тождественно нулю и удовлетворяющие равенству:

ψ (r ) +ωψ (r ) = 0 ,	(3.64)
где параметр ω выбирается таким,	чтобы уравнение (3.63)
обращалось в тождество.

Полагая φ(1) (r ) = Cψ (r ) и учитывая (3.64), установим, что значения ω должны совпадать с корнями квадратного уравнения:

−1

−ε

−

K∞

= 0 .

(3.65)

L τc

Дискриминант

этого

уравнения

δ = (

−

4K∞

> 0 .

L τc

Поэтому

корни

ω = ω1 ,

ω = ω2

являются

действительными,

различными и определяются равенствами:

4(К∞ −1−ε) τ L

−1 +

(1+ε) (τ + L2 )2

(3.66)

ω2

= −

4 (К∞ −1−ε)τ L

1 +

(1+ε) (τ + L )

Зависимости ω1 и ω2 от

размножающих свойств зоны (K∞ )

приведены на рис.3.2 (для случая, когда L2 <τ ). Видно, что

ω1

≥ 0 при

+ε ,

< 0 при K∞ <1 +ε

∞ ≥1

ω2

< 0 при K∞ ≥ 0 .

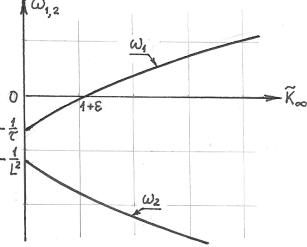
Рис.3.2. Зависимости корней уравнения (3.65) от

		~
величины коэффициента		К∞ .
Таким образом, функции	ψ1 (r ) ,	ψ2 (r ) , удовлетворяющие
уравнениям
ψ1 (r ) +ω1ψ1 (r ) = 0 ,	ψ2 (r ) +ω2ψ2 (r ) = 0 ,		(3.67)

являются частными решениями бигармонического уравнения

(3.65). Поэтому общие решения													для		потоков	φ(1) (r ) ,	φ(2) (r )
записываются в виде:
φ(1) (r ) = A(1)ψ							1	(r ) + A(1)ψ			2		(r ) ,
					1		1		2		2						(3.68)
φ(2) (r ) = A(2)ψ								(r ) + A(2)ψ						(r ) ,			(3.68)
φ(2) (r ) = A(2)ψ							1	(r ) + A(2)ψ				2		(r ) ,
					1		1		2			2
где А(1) , А(2) , А(1) ,						А(2) – постоянные множители, из которых два
1	2				2		1
множителя			(например					А(1)	и		А(2) )				могут принимать		любые
								1					2
значения, а остальные зависят от них.
Действительно,						подставляя в								уравнение		(3.62)	сначала
φ(1) = А(1)ψ	1		(r ) ,		φ(2)			= А(2)ψ	1	(r ) ,				а	затем	φ(1) = А(1)ψ		2	(r ) ,
1	1							1	1							2		2
φ(2) = А(2)ψ		2		(r )	получим тождество, когда
2		2
										84

(2)			(1)	,	(1)	~	(2)	,
A1	= p A1			,	A2	= p A2		,
p =			ϕΣ(1)d			~		(1+ω2 L2 )Σ(a2)
						, p	=			.	(3.68)
	Σ	(2)			2	, p	=	ϕ Σ	(1)	.	(3.68)
	Σ	a	(1+ω L )					ϕ Σ	d
		a			1				d

Очевидно, в обоих случаях выполняется также равенство (3.61), так как ω1 , ω2 – корни уравнения (3.65).

Теперь можно приступить к получению условия критичности и асимптотических распределений нейтронов. Эта часть условнокритической задачи решается так же, как в односкоростном

приближении. Однако выражения для потоков φ(1) (r ) и φ(2) (r )

(зависящих в любой одномерной геометрии от одной переменной r ) должны быть записаны, учитывая соотношения (3.69) и вид частных решений уравнений (3.67). Соответствующие функции приведены в табл.1.1.


Предположим,		что любую зону с номером							i =1, 2,... можно
считать либо активной зоной с					~ (i)	>1 +εi , либо отражателем с
					K∞
~ (i)	= 0 . Разобьем		множество			I	номеров зон			на	два
K∞
подмножества I p		и	I0 ,	включив			в	I p	номера	активных
(размножающих) зон,			а в	I0	– номера			неразмножающих			зон

(отражателей). Введем для корней ω1 ,

ω2 в i -й зоне обозначения:

ω = β 2

= −γ 2

если i I

;

ω = −υ

= −

, ω

= −ϑ2

= −

, если i I

а для частных решений уравнений (3.67) в той же зоне –

обозначения:			~	~
f (βi r) ,	g(βi r)	и			I p
			f (γi r) , g(γi r) , если i
~	~	и	~	~	I0 .
f (υi r) ,	g(υi r)		f (ϑi r) ,	g(ϑi r) , если i
Тогда потоки быстрых φ(1) (r)				и тепловых φ(2) (r) нейтронов в
i -й зоне (толщиной Ri		= Ri − Ri−1 ) принимают вид:

если i I p , то для r Ri :

(1)			~	~	~
φi	(r) = ai f (βi r) + bi g(βi r) + pi			[ci f (γi r) + di g (γi r)],
(2)	(r) = pi [ai f (βi r) + bi g(βi r)]			~	~
φi	(r) = pi [ai f (βi r) + bi g(βi r)]			+ ci f (γi r) + di g(γi r) ;
если i I0 , то для		r Ri :				(3.70)
(1)	~	~
φi (r) = ai f (υi r) +bi g(υi r) ,				~	~
(2)	~	~		~	~
φi	(r) = pi [ai f (υi r)	+bi g(υir)]+ ci f (ϑi r) + di g(ϑi r) ,
где	ai , bi , ci , di – произвольные множители,					независящие от
		~	–	коэффициенты		связи (3.69),
переменной r , pi , pi			–	коэффициенты		связи (3.69),
рассчитываемые по свойствам i -й зоны.

Значения неизвестных ai , bi , ci , di получим, используя

граничные условия, а также	условия непрерывности потоков
φ(к) (r ) и проекций токовD(k )	dφ(k )	(k =1,2) на границах зон. В
	dr

результате придем к системе линейных (относительно перечисленных выше неизвестных) однородных уравнений с определителем Д(и) , зависящим от параметров u реактора. Из

равенства Д(и) = 0 получим критические значения и = и0 параметров, а затем (как и в односкоростном приближении) определим для всех зон множители ai , bi , ci , di , предварительно приняв один из них равным единице. После этого по формулам (3.70) рассчитаем асимптотические распределения потоков φ(1) (r) ,

φ(2) (r) . При этом возникают те же проблемы, которые обсуждались в разделе 2.2.

3.6. Распределения нейтронов в реакторе с отражателем

Воспользуемся полученными выше соотношениями для определения критического размера сферически симметричного реактора. Рассмотрим сначала случай, когда имеется одна активная

зона, а при r = Rэ располагается экстраполированная граница.

Тогда потоки нейтронов в активной зоне φ1(1) (r) , φ1(2) (r) должны удовлетворять условиям:

	r	2 dφ(k )		= 0	, φ	(k )	(R ) = 0 , к =1,2 ,	(3.71)
	r			= 0	, φ		(R ) = 0 , к =1,2 ,	(3.71)
		dr			1		э
		dr	r=0
0 ≤φ(k ) (r) < ∞ при 0 ≤ r ≤ R ,
		1					э

а частными решениями уравнений (3.67) являются следующие функции:

		f (β1r) =						sin(β1r)								, g(β1r) =				cos(β1r)			,
		f (β1r) =									β1r					, g(β1r) =				β1r			,
											β1r									β1r
	~						sh(γ1r)									~		ch(γ1r)
	f (γ1r) =														,	g(γ1r) =						,			(3.72)
	f (γ1r) =									γ1r					,	g(γ1r) =				γ1r		,			(3.72)
										γ1r										γ1r
		1		1			1																2
где β2	=	1		1	+		1					−1			+	1+	4(К∞ −1−ε) τ1 L1							,
где β2	=	2			+		τ					−1			+	1+	4(К∞ −1−ε) τ1 L1							,
1		2	L2				τ		1								(1+		ε) (L2		+τ		)2
				1					1										1			1

		1		1					1														2
γ 2	=	1		1		+			1				1	+		1+	4 (К∞ −1−ε)τ1 L1							.	(3.73)
γ 2	=	2				+	τ						1	+		1+	4 (К∞ −1−ε)τ1 L1							.	(3.73)
1		2	L2				τ										(1+		ε) (L2		+τ		)
				1						1									1			1

Однако не все функции (3.72) войдут в выражения (3.70) для

потоков

φ (1) (r) ,

(2)

(r) .

Необходимо учитывать,

что

любая

sin(β1r)

cos(β1r)

функция

вида

ψ (r)

= a

или

β r

ψ (r) = c

sh(γ1r)

+ d

ch(γ1r)

являющаяся

решением

уравнения

γ r

(3.64), должна удовлетворять равенствам (3.71). Нетрудно установить, что первое из них (при r = 0 ) будет выполнено, если b1 = 0 и d1 = 0 , а второе (при r = Rэ ) – если с1 = 0 и sin(β1Rэ) = 0 . В результате для определения критического радиуса получим соотношение:

β1Rэ = π .

(3.74)

Таким образом, асимптотические распределения потоков имеют вид:

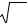
φ(1)	(r) = a	sin(β1r)	,	φ(2)	(r) = a p	sin(β1r)	.	(3.75)
		β1r
1	1			1	1 1	β1r

Это согласуется с представление многогрупповых потоков в форме (3.55) и приводит к тому, что:

φ(2) (r)		= p1 =		ϕ1Σ(1)d ,1
1						.	(3.76)
φ(1)	(r)		Σ(2)	(1 + β	2 L2 )	.	(3.76)
1			a,1		1 1

Поскольку обычно в активной зоне теплового реактора из-за сильного поглощения тепловых нейтронов топливом Σ(a2,1) > Σ(d1,)1 ,

ϕ1 <1, то значение p1 <1, и следовательно, в реакторе без отражателя при всех 0 ≤ r ≤ Rэ поток тепловых нейтронов меньше

потока быстрых нейтронов.

Чтобы выяснить влияние отражателя на распределение нейтронов, рассмотрим реактор, состоящий из активной зоны радиуса R , окруженной бесконечным отражателем. В таком реакторе должны выполняться условия:

r 2

dφ1(k )

= 0 ,

0 ≤ φ(k ) < ∞ ,

0 ≤ φ

( k ) (r) < ∞,

(3.77)

r=0

φ(k ) (R) =φ

(k ) (R),

D(k )

dφ(k )

= D(k )

dφ( k )

(3.78)

r=R

а при

построении

зависимостей

φ(1) (r) , φ(2) (r)

наряду с

функциями (3.72) могут рассматриваться (при R ≤ r ):

(υ2r)

exp (−υ2r) ,

(υ2r) =

exp (υ2r) ,

υ2 r

υ2r

(ϑ2r)

exp(−ϑ2r) ,

(ϑ2r) =

exp(ϑ2r) ,

ϑ2 r

где

υ2

ϑ2

Здесь

учтено,

что

в неограниченно

протяженных зонах без размножения вместо гиперболических функций sh(αr) , ch(αr) следует брать экспоненты exp(−αr) , exp(αr) .

Так же, как в реакторе без отражателя, для выполнения условия (3.77) при r = 0 необходимо в выражениях (3.70) для потоков в активной зоне принять b1 = 0 , d 1= 0 . Из условий ограниченности

решений на

бесконечности

следует,

что в отражателе

b2 = 0 ,

d 2= 0 . Поэтому имеем:

(1)

(r) = a1

sin(β1r)

sh(γ1r)

φ1

+ p1c1

0 ≤ r ≤ R ,

β1r

γ1r

φ(2) (r) = p a

sin(β1r)

+ c

sh(γ1r)

0 ≤ r ≤ R ,

(3.79)

β1r

γ1r

φ(1)

(r) = a

exp(−υ

r) ,

R ≤ r < ∞ ,

2 υ2r

φ(2)

(r) = p

exp(−υ

r) + c

exp(−ϑ r) , R ≤ r < ∞ ,

2 υ

2 ϑ r

где параметры β1 и γ1 по-прежнему рассматриваются по формулам (3.73), а коэффициенты связи определяются равенствами

ϕ1Σ(1)d ,1

(1−γ12 L12 ) Σ(a2),1

Σ(1)d ,2 τ2

p1 =

, p2 =

Σ(2)

(1 + β 2 L2 )

ϕ Σ(2)

Σ(2)

(τ

− L2 )

a,1

1 1

d ,1

a,2

a1 ,

c1 ,

a2 ,

(3.80)

Коэффициенты

находятся,

используя

соотношения (3.78) между потоками и токами нейтронов на границе r = R . Получаемое при этом условие критичности реактора имеет достаточно сложный вид. Известно [5], что его

можно существенно упростить, если принять следующие допущения: в активной зоне и отражателе один и тот же замедлитель, отсутствует поглощение замедляющихся нейтронов, а активная зона имеет достаточно большие размеры. В этом случае

можно	считать, что τ	1	=τ	2	=τ , D(1)		= D(1) ,	Σ(1)	= Σ(1) = 0 ,
		1		2		1	2	a,1	a,2
ν (f1)Σ(f1,)1	= 0 , γ1 R >>1. Тогда,				вводя в рассмотрение эффективную
добавку δ = R − R (где R =					π	– критический радиус реактора
добавку δ = R − R (где R =					β	– критический радиус реактора
	э		э		β
					1

без отражателя), условие критичности принимает вид:

β δ = arctg(β L ) + arctg(β

τ ) −arctg β1

(3.81)

γ1

откуда

нетрудно

оценить

критический

радиус

реактора

отражателем.

Выражения

(3.79)

для потоков

нейтронов (в случае,

когда

D(1)

= D(1) ) могут быть преобразованы к виду:

φ(1)

(r) = a

sin(β1r)

−η

sh(γ1r)

β1r

γ1r

(2) (r) = a p

sin(β1r)

−

η1

sh(γ1r)

β1r

γ1r

p1 p1

(1)

r − R

(r) = φ

(R)

exp −

(3.82)

(2)

(1)

r − R

(2)

(R)

r − R

φ1

φ2

(r) = p2 φ1

(R)

exp −

−1 exp

−

φ(1) (R)

cos(β δ)

tg(

β δ)

где

−1 ,

β1 sh(γ1R) +γ1 τ2 ch(γ1R)

β1

τ2

1 −γ12 L12

p1 p1

< 0 ,

0 <η1 <<1 .

1 + β

2 L2

Последнее неравенство (для η1 ) нетрудно установить, если наряду с ранее принятыми допущениями (при которых имеет место

формула (3.81) для δ ) считать, что: β1 L2 <1, β1 τ <1, L2 > L1 ,

δ < 12 Rэ .

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 169 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.20132.37 Mб194Крючков Технические аспекты ядерного нераспространения 2010.pdf
#
16.08.2013864.18 Кб34Ктитров Администрирование ОЦ УНИХ 2007.pdf
#
16.08.20131.06 Mб53Ктитров Командный язык ОЦ Уних 2007.pdf
#
16.08.20131.93 Mб133Ктитров Расчет установившихся режимов и переходных процессов в нелинейных 2008.pdf
#
16.08.20131.5 Mб511Кудряшов Методы нелинейной математич 2008.pdf
#
16.08.20131.51 Mб193КузминАМ Основы теории критичности 2008.pdf
#
16.08.20131.79 Mб77Кулик Елементы теории принятия решений 2010.pdf
#
16.08.20131.87 Mб99Кулик Теория принятия решений 2007.pdf
#
16.08.201310.8 Mб221Курнаев Введение в пучковую електронику 2008.pdf
#
16.08.201310.79 Mб69Лабораторный практикум Компютерное модел 2007.pdf
#
16.08.20132.27 Mб50Лабораторный практикум Механика твёрдого тела 2002.pdf