
КузминАМ Основы теории критичности 2008
.pdf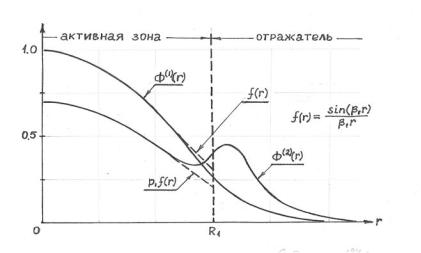
Рис.3.3. Распределения потоков быстрых φ(1) (r) и тепловых
φ(2) (r) нейтронов в реакторе с отражателем
Анализ выражений (3.82) показывает, что
- в активной зоне вдали от границы с отражателем ( r = R ) потоки φ1(1) (r) , φ1(2) (r) (как и в реакторе без отражателя)
пропорциональны одной и той же функции f (r) = sin(β1r) ;
β1r
- по мере приближения к границе r = R поток тепловых нейтронов
φ(2) (r) |
возрастает, |
|
|
а |
поток |
|
быстрых |
нейтронов |
φ(1) (r) |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 f (r) |
|
1 |
уменьшается |
|
|
|
относительно |
значений |
и |
f (r) , |
|||||||||||
соответственно; поэтому: |
|
|
|
|
|
|
|
|
||||||||||
|
|
φ1(1) (R) |
< |
|
φ1(1) |
|
= |
|
1 |
, |
|
|
(3.83) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
φ |
(2) |
(R) |
φ |
(2) |
|
p |
|
|
|||||||||
|
|
|
|
|
|
б / o |
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|||||
φ(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
– |
отношение потоков в реакторе без |
отражателя, |
|||||||||||||
где φ(2) |
|
|||||||||||||||||
1 |
б / o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
совпадающее с (3.76);
91

-может оказаться, что в отражателе поток тепловых нейтронов
φ2(2) (r) по мере удаления от r = R начнет расти и достигнет при
некотором значении r = R |
максимального значения φ( 2) |
(R ) ; это |
|||||||||||||
|
|
|
|
|
|
|
ο |
|
|
|
|
|
|
2 |
ο |
|
|
|
dφ( 2) |
|
|
> 0 , что эквивалентно условию: |
|||||||||
|
|
|
|
|
|||||||||||
возможно когда |
|
2 |
|
|
|
||||||||||
dr |
|
|
r=R |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
φ(1) |
|
|
|
|
|
|
|
|
|
|
|
Σ(a2),2 |
|
|
|
(R) |
|
|
|
|
L |
|
|
L |
|
|
|
||||
1 |
|
> 1 |
+ |
|
2 |
|
1 |
+ |
2 |
|
|
. |
(3.84) |
||
(R) |
R |
|
Σ(1) |
||||||||||||
φ(2) |
|
|
|
|
|
|
|
τ |
2 |
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
d ,2 |
|
|
|
Учитывая неравенства (3.83), (3.84) и принимая во внимание выражения (3.74) и (3.80), приходим к соотношению:
|
|
|
2 |
|
L1 |
2 |
|
|
|
|
|
|
|
||
Σ(2) 1+π |
|
|
|
|
|
|
|
Σ(2) |
|||||||
|
|
|
|
L |
|
||||||||||
|
R |
|
|
|
|||||||||||
a,1 |
|
|
|
|
э |
> 1 |
+ |
2 |
|
a,2 |
. |
||||
ϕ Σ(1) |
|
|
|
|
|
|
|
||||||||
1 |
+ |
|
L2 |
|
|
|
τ |
|
|
Σ(1) |
|||||
1 d ,1 |
|
|
R |
|
|
|
|
2 |
|
d ,2 |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
Оно показывает, что рост потока тепловых нейтронов в отражателе можно ожидать в реакторе с небольшим размером активной зоны и отражателем, имеющим высокую замедляющую способность и низкое поглощение тепловых нейтронов. Отличенные особенности
отражены на рис.10, где приведены зависимости φ(1) (r) и φ(2) (r) для реактора с указанными выше свойствами.
3.7. Условно-критическая задача в P1 - приближении
Задачи о критичности многозонного реактора обычно решаются, используя метод итераций источников. Этот метод, изложенный в разделе 2.4 для односкоростной модели, нетрудно обобщить на случай многогрупповых моделей. Отличие будет состоять лишь в том, что теперь на каждой n -й итерации вместо одного уравнения вида (2.37) решается система уравнений для потоков нейтронов φn(k ) (r) Ω(k ) n -го поколения ( k =1, 2,…, m ):
k−1
divJ (k ) (r ) +Σ(k )φ(k ) (r ) = ∑Σ( j→k )φ( j) (r ) + χ(k )q − (r) . (3.85) n ad n d п n 1
j=1
92
m |
|
Здесь распределение источников qn−1 (r ) = ∑ν (fk ) Σ(jk )φn(−k1) (r ) |
|
k =1 |
|
известно, а токи нейтронов того же поколения J n(k ) (r ) |
могут быть |
связаны с потоками φn(k ) (r ) соотношениями: |
|
gradφn( k ) (r ) +3Σtr( k ) Jn(k ) (r ) = 0 , k =1,2..m , |
(3.86) |
если рассматривается диффузионное приближение (3.36), и соотношениями:
k−1
grad φn(k ) (r ) + 3Σ(t1k ) Jn(k ) (r ) = 3∑Σ(dj1→k ) j=1
Jn( j) (r ) , |
(3.87) |
если рассматривается P1 -приближение (3.41).
Как и в односкоростной модели, итерации прекращают, когда при заданной погрешности ε > 0 выполнится неравенство вида
(2.38). Полученные на последней итерации n = p значение K ( p) и
функции φp(k ) (r ) |
принимаются в |
качестве |
решения |
условно- |
||||
критической задачи: |
|
|
|
|
|
|
||
Kэф = K ( p) , |
φ(k ) (r ) = Cφp(k ) (r ) , |
|
k =1, 2,…, m . |
(3.88) |
||||
Также рекомендуется на 1-й итерации источник q0 (r ) |
задавать в |
|||||||
виде неотрицательной |
функции, |
а |
для |
(n +1) -й |
итерации |
|||
|
|
|
1 |
m |
|
|
||
рассчитывать по формуле: |
qn (r ) = |
∑ν (fk ) Σ(jk )φn(k ) (r ) . |
||||||
(n) |
||||||||
|
|
|
K |
|
k =1 |
|
|
|
Каждое из уравнений (3.85) совпадает по форме с уравнением (2.37) односкоростной модели и решается численно с использованием известных алгоритмов. В случае диффузионного приближения, когда принимаются соотношения (3.86), можно воспользоваться алгоритмами, изложенными в разделах 2.4 и 2.5.
При использовании Р1 -приближения и соотношений (3.87) они
претерпевают незначительные изменения. Поясним их на примере многозонного реактора в одной из простых одномерных геометрий.
Уравнения (3.85), (3.87) для k -й группы нейтронов запишем в виде 2-х дифференциальных уравнений 1-го порядка (индексы группы и номера итераций опущены):
93

|
d(rν J (r)) |
+ r |
ν |
Σ(r)φ(r) |
ν |
q(r) , |
|
(3.89) |
|
|
|
dr |
|
= r |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
dφ(r) |
~ |
|
|
~ |
|
|
|
|
|
|
dr |
+3Σ(r) J (r) = 3q (r) , |
~ |
|
(3.90) |
|
||||
где макроскопические сечения Σ(r) , |
|
|
|
|||||||
Σ(r) и распределения q(r) , |
||||||||||
~ |
терпят разрывы на границах зон, поток φ(r) |
и проекция тока |
||||||||
q (r) |
||||||||||
J (r) |
непрерывны при всех значениях 0 ≤ r ≤ Rэ |
и удовлетворяют |
||||||||
условиям J (0) = 0 , φ(Rэ) = 0. |
|
|
r |
основные |
и |
|||||
Разместив в области изменения переменной |
||||||||||
вспомогательные |
точки с |
координатами |
rl |
< rl+(1 / 2) < rl+1 |
||||||
(l =1, 2,...) , |
проинтегрируем |
|
уравнение |
|
(3.89) |
по |
||||
r [rl−(1 / 2) , rl+(1 / 2) ], а уравнение (3.90) – по r [re , re+1 ]. Проведя с
полученными равенствами те же преобразования, что и в разделе 2.4, придем к конечно-разностным уравнениям:
rν |
J |
l−(1 / 2) |
− rν |
J |
l+(1 / 2) |
− Σ φ |
||||
l−(1 / 2) |
|
l+(1 / 2) |
|
|
l l |
|||||
|
|
|
|
φl −φl+1 |
|
|
~ |
|
||
Jl+(1 / 2) |
= |
|
|
|
+ |
ql+(1 / 2) |
, |
|||
~ |
|
|
|
~ |
||||||
|
|
|
3Σl+(1 / 2) rl+(1 / 2) |
|
Σl+(1 / 2) |
|
||||
Vl = − q l Vl , |
(3.91) |
l =1, 2,…, |
(3.92) |
~ |
~ |
(rl+(1 / 2) ) , |
φl = φ(rl ) , Jl+(1 / 2) = J (rl+(1 / 2) , |
где ql+(1 / 2) |
= q |
~ |
~ |
|
|
Σl+(1 / 2 ) |
= Σ(rl+(1 / 2) ) , а |
остальные |
обозначения совпадают с |
принятыми в разделе |
2.4. Если |
теперь из уравнения (3.91) |
|
исключить Jl−(1 / 2) , Jl+(1 / 2) , используя для них соотношения (3.92), то получим систему 3-точечных уравнений, отличающихся от
равенств (2.54) лишь способом расчёта источников |
fl : |
||||||
|
|
~ |
|
~ |
|
|
|
|
|
|
q |
|
q |
|
|
fl = q l |
Vl |
− rlν+(1 / 2) |
~l+(1 / 2) |
+ rlν−(1 / 2) |
~l−(1 / 2) |
. |
(3.93) |
|
|
|
Σl+(1 / 2) |
|
Σl−(1 / 2) |
|
|
Такая система легко решается методом прогонки.
Если при использовании диффузионного приближения всегда fl ≥ 0 , то теперь не исключается появление отрицательных
значений для источников fl и, возможно, для потоков φe . Как
94
видно из выражения (3.93), необходимым (но не достаточным) условием для получения φl < 0 будет выполнение неравенства:
~ |
r |
ν |
~ |
|||
q |
|
|
q |
|
||
~l+(1 / 2) |
− l−(1 / 2) |
|
~l−(1 / 2) |
|||
Σ |
l+(1 / 2) |
|
r |
|
Σ |
l−(1 / 2) |
|
l+(1 / 2) |
|
|
|||
что имеет место, когда или значения
> q l Vl ,
~ |
~ |
Σl+(1 / 2) |
и Σl−(1 / 2) |
различаются, либо проекция тока (от которой зависят
сильно
q~l+(1 / 2) )
намного превышает поток нейтронов (от которого зависит q l ).
Но при этом не применимо P1 -приближение и, следовательно, надо переходить к более точному описанию распределения нейтронов.
Глава 4. ТЕОРИЯ ВОЗМУЩЕНИЙ ДЛЯ КОЭФФИЦИЕНТА РАЗМНОЖЕНИЯ НЕЙТРОНОВ
В практике расчётов ядерных реакторов часто требуется найти изменения различных физических характеристик, вызванные небольшими отклонениями технологических параметров: концентраций ядер, микроскопических сечений, температур и т.п. В общем случае эта задача решается с помощью методов теории возмущений, использующей такие понятия, как сопряжённые операторы и сопряжённые функции.
Определение. Пусть ˆ – линейный оператор, определённый на
M
функциях ϕ Ω Н , принадлежащих некоторому плотному в гильбертовом пространстве Н множеству Ω . Тогда сопряжённым к Мˆ называют такой оператор Мˆ + , определённый на функциях ϕ+ Ω+ Н , что выполняется тождество:
+ |
ˆ |
= |
ˆ + + |
,ϕ , |
(4.1) |
ϕ |
, Мϕ |
М ϕ |
где скобки 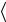 ,
,  обозначают скалярное произведение стоящих
обозначают скалярное произведение стоящих
внутри них и разделённых запятой функций.
Опираясь на определение (4.1), можно любому оператору линейного уравнения переноса нейтронов, записанному в какомлибо приближении, поставить в соответствие сопряжённый
95
оператор. В результате придём к сопряжённому уравнению реактора относительно сопряжённой функции ϕ+ , принадлежащей
множеству |
Ω+ Н |
и |
позволяющей |
(при |
известном |
|
распределении |
нейтронов) |
изменения |
рассматриваемой |
|||
характеристики |
реактора |
выразить |
через |
отклонения |
||
технологических параметров.
В этом разделе изложенный выше подход использован для получения изменения δКэф эффективного коэффициента
размножения нейтронов Кэф . При этом считается, что реактор состоит из нескольких зон разного состава, а Кэф и
асимптотические потоки нейтронов φ( к) (r ) находятся из решения
условно-критической задачи (3.32), (3.36), (3.43) в многогрупповом диффузионном приближении. Микроскопические сечения определяются по формулам (3.38) и не меняются при изменении технологических параметров.
Основные уравнения рассматриваемого приближения для потоков φ( k ) (r ) перепишем в виде:
− div J (k ) (r ) −Σ(adk ) φ(k ) (r ) +
k−1 |
1 |
m |
|
|
|
+ ∑Σ(dj→k ) φ( j) (r ) + |
χ(k ) ∑ν (fl )Σ(fl ) φ(l ) (r ) = 0 , |
(4.2) |
|||
Kэф |
|||||
j=1 |
l=1 |
|
|
||
3Σ(trk ) J ( k ) (r ) + grad φ( k ) (r ) = 0 , |
k =1, 2,…, m , |
(4.3) |
|||
приняв те же обозначения для макроскопических сечений в k-х энергетических группах Σ(adk ) , Σ(dj→k ) , Σ(trk ) ,ν (fk )Σ(fk ) , χ(k ) , что и в разделе 3.1. Как и раньше, будем считать, что решения уравнений
(4.2), (4.3) |
ищутся среди функций φ(k ) (r ) Ωk , |
а множества Ωk |
описываются условиями: |
|
|
φ( k ) (r ) , |
(J ( k ) (r ) , n)– непрерывны при r V , |
|
φ(k ) (rэ) =0, k =1,…m . |
(4.4) |
|
Здесь n – единичный вектор нормали к границе раздела двух сред, а rэ – радиус-вектор точек экстраполированной границы.
96
4.1. Основные соотношения теории возмущений
Пусть u = (u1 ,u2 ,…un )T – вектор технологических параметров с известными компонентами u j ( j = 1, 2,…n) , которым
соответствуют определённые значения размеров зон и макроскопических сечений. Из решения системы уравнений (4.2),
(4.3) при условиях (4.4) получены значение Кэф и распределения
φ(k ) (r ), J (k ) (r ) . Предположим, что затем произошло изменение одного или нескольких технологических параметров до значений u′j =u j +δu j . Это повлечёт за собой изменения макроскопических
сечений (в одной или нескольких зонах, а может быть – в какойлибо части отдельной зоны) до значений:
Σ′(k ) = Σ(k ) +δΣ(k ) , |
Σ′(k ) = Σ(k ) |
+δΣ(k ) |
, Σ′( j→k ) |
= Σ( j→k ) +δΣ( j→k ) , |
|||||||
tr |
tr |
tr |
ad |
|
ad |
ad |
d |
|
d |
d |
|
ν′f(k )Σ′f(k ) |
=ν (fk )Σ(fk ) +δ (ν(fk )Σ(fk ) ). |
|
|
|
|
(4.5) |
|||||
В результате изменится решение задачи (4.2) – (4.4): |
|
||||||||||
|
Кэф = Кэф +δКэф , φ |
′(k ) |
(r ) = φ |
|
(r ) +δφ |
|
(r ) , |
|
|||
|
′ |
|
|
|
|
(k ) |
|
(k ) |
|
|
|
|
J ′(k ) (r ) = J (k ) (r ) +δJ (k ) (r ) . |
|
|
|
|
|
(4.6) |
||||
Реактор с первоначально заданным вектором u технологических параметров будем называть невозмущённым
реактором, |
реактор с изменённым |
вектором |
u′ = u +δu – |
|||||||||
возмущённым |
реактором, |
а |
изменение |
δu – |
возмущением |
|||||||
реактора. Новые значения |
′ |
|
′(k ) |
(r ) , J |
′(k ) |
(r ) |
удовлетворяют |
|||||
Кэф , φ |
|
|
||||||||||
уравнениям: |
− div J |
′(k ) |
|
|
′(k ) |
|
′(k ) |
(r ) + |
|
|
||
|
(r ) −Σad φ |
|
|
|
|
|||||||
k−1 |
1 |
|
|
+ ∑Σ′d( j→k )φ′( j) (r ) + |
χ |
||
′ |
|||
j=1 |
|
||
Кэф |
|
m |
|
(k ) ∑ν′f(l)Σ′f(l)φ′(l ) (r ) = 0 , |
(4.7) |
l=1
3Σ′tr(k ) J′(k ) (r ) + gradφ′(k ) (r ) = 0 , |
k =1, 2,…, m |
(4.8) |
и ищутся при условиях φ′(k ) (r ) Ωk , |
k =1, 2,…, m . |
(4.9) |
Принимается, что с изменением технологических параметров спектр нейтронов деления χ(k ) , k =1, 2,…m , и область V
97
изменения аргументов r не меняются. Получение эффективного коэффициента размножения и асимптотических потоков нейтронов путём решения уравнений (4.2) - (4.4) для невозмущённого реактора будем называть невозмущённой задачей, а нахождение тех же характеристик из решения уравнений (4.7) - (4.9) – возмущённой задачей.
Изменение δКэф = Кэф′ − Кэф можно получить при заданном отклонении δu j = u′j −u j технологических параметров, не
прибегая, вообще говоря, к методам теории возмущений. Для этого возмущённую задачу (4.7) - (4.9) достаточно решить столько раз, сколько вносится в реактор различных возмущений. Например,
если требуется определить изменения δКэф , происходящие при
изменении каждого из n технологических параметров, то следует помимо одной невозмущённой задачи (4.2) – (4.4) решить n
возмущённых задач вида (4.7) - (4.9), задавая для каждой из них |
|||||
вектор |
u′ = u ( j) |
= (u1, u2 ,…u j−1 , u j +δu j , u j+1,…un )T , |
|||
j = 1,2,…n , |
и |
получая |
соответствующие |
значения |
|
Кэф = Кэф( j) , |
|
δКэф( j) = Кэф( j) − Кэф . |
Такой способ будем |
называть |
|
разностным |
|
методом |
определения δКэф . Он имеет следующие |
||
недостатки:
1. Если n велико, то придётся потратить много времени для нахождения всех значений δКэф( j) , j =1, 2,…,n . Например,
это имеет место, когда в качестве возмущений рассматриваются изменения микроскопических сечений, а расчёты проводятся в 26групповом приближении.
2.Если погрешность ε определения значений Кэф , Кэф′ при решении задач (4.2) - (4.4) и (4.7) - (4.9) сравнима с
изменением δКэф (т.е. |
δКэф |
≈ ε ), то можно получить |
|
неправильное представление о зависимости δКэф |
от δu j . |
||
Это может случиться, |
когда изменения δu j |
малы, |
|
например, при нахождении температурных коэффициентов реактивности.
98

Введём в рассмотрение функции φ+(k ) (r ) и векторные функции
J +(k ) (r ) = J x+(k )ex + J y+(k )ey + J z+(k )ez |
(k =1,2,…, m) |
с |
||
проекциями Jx+(k ) (r ) , J y+(k ) (r ) , Jz+(k ) (r ) |
на координатные |
оси |
||
x , y , z |
соответственно ( ex , ey , ez |
– единичные орты). Будем |
||
считать, |
что они определены |
при |
значениях r V |
и |
удовлетворяют условиям: |
|
|
φ+(k ) (r ), |
(J +(k ) (r ), n)– непрерывны при |
r V ; |
φ+(k ) (r ) = 0 . |
(4.10) |
|
э |
|
|
Умножая уравнения (4.7) на φ+(k ) (r ) , а уравнения (4.8) – скалярно
на функции J +(k ) (r ) , интегрируя по переменным r V и складывая, получим:
∑m ∫φ+(k ) (r ) [− divJ
k=1 V
r−1
+∑Σ′d( j→k )φ′( j) (r j=1
+∑m ∫(J +(k ) (r ) , 3Σ′tr(k )
k =1 V
′(k ) (r ) −Σ′ad(k ) φ′(k ) (r ) +
) + ′ |
χ |
|
m |
|
Σ′f φ′ |
|
(r ) dV + |
|
|
(k ) |
∑ν′f |
(l ) |
(l ) |
|
|||||
1 |
|
|
(l ) |
|
|
||||
|
Кэф |
|
|
l=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J ′(k ) (r ) + grad φ′(k ) (r ))dV = 0 . |
(4.11) |
||||||||
Преобразуем выражение (4.11), используя формулу Грина:
∫div(f (r )g(r ))dV =∫ f (r ) div g(r ) dV + ∫(g(r ), grad f (r ))dV =
V |
V |
V |
|
|
= ∫ f (rs ) (g(rs ), n)dS , |
(4.12) |
|
S
где S – поверхность, ограничивающая объём V, n – единичный вектор внешней нормали, а f (r ), g(r ) – непрерывные вместе со
своими частными производными 1-го порядка функции радиусвектора точки r . Учитывая при этом условия (4.4) и (4.10), будем иметь:
99
∫φ+(k ) (r ) divJ′(k ) (r )dV = −∫(J′(k ) (r ), gradφ+(k ) (r ))dV
V |
V |
. (4.13) |
∫(J +(k ) (r ), gradφ′(k ) (r ))dV = −∫φ′(k ) (r ) divJ +(k ) (r )dV |
||
V |
V |
|
Кроме того, меняя порядок суммирования, получим:
m |
k −1 |
m |
m |
∑φ+(k ) (r )∑Σ′d( j→k )φ′( j ) (r ) = ∑φ′(k ) (r ) ∑Σ′d(k → j)φ+( j ) (r ) . (4.14) |
|||
k =1 |
j =1 |
k =1 |
j =k +1 |
Возмущённые значения макроскопических сечений заменим суммами (4.5), воспользуемся равенствами (4.6), а среди функций, удовлетворяющих условиям (4.10), выберем такие, которые будут решениями уравнений:
|
|
|
|
|
|
|
|
m |
|
|
|
− divJ +(k ) (r ) −Σ(adk ) φ+(k ) (r ) + ∑Σ(dk→ j)φ+(k ) (r ) + |
|||||||||||
|
|
|
|
|
|
|
|
j=k+1 |
|
|
|
|
|
|
1 |
|
m |
|
|
|
|
|
|
+ |
|
ν (fk )Σ(fk ) ∑χ(l )φ |
+(l ) (r ) = 0 , |
|
|
||||||
|
Кэф |
|
|
||||||||
|
|
|
|
l=1 |
|
|
|
|
|
||
3Σtr(k ) J +(k ) (r ) + gradφ+(k ) (r ) = 0 , k =1, 2,…, m . |
|||||||||||
В результате придём к равенству: |
|
|
|
||||||||
|
|
|
|
|
|
m |
(J |
|
|
|
(r ))dV + |
|
|
|
|
|
= ∑∫3δΣtr |
|
(r ), J ′ |
|
|||
|
|
|
|
|
|||||||
−δ |
|
G′f |
+(k ) |
(k ) |
|||||||
1 |
|
|
+ |
(k ) |
|
|
|
||||
Кэф |
|
|
|
k=1 V |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
k−1 |
+ ∑∫φ |
+(k ) (r ) −δΣ(adk )φ′(k ) (r ) + ∑δΣ(dj→k )φ′(k ) (r ) + |
||||||||
k=1 V |
|
|
|
|
|
|
|
j=1 |
|
+ |
1 |
|
χ |
|
m |
Σf |
)φ′ |
|
(r ) dV , |
|
(k ) |
∑δ(ν f |
(k ) |
||||||
|
|
|
(k ) |
(k ) |
|
|
|||
|
Кэф |
|
l=1 |
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
m |
|
|
m |
|
в котором G′f+ = ∫∑χ(k )φ+(k ) (r ) ∑ν (fl )Σ(fl )φ′(l ) (r ) dV . |
|||||||||
|
|
|
|
V |
k=1 |
|
l=1 |
|
|
(4.15)
(4.16)
(4.17)
Уравнения (4.15), (4.16) будем называть сопряжёнными уравнениями условно-критического (невозмущённого) реактора, а выражение (4.17) – точной формулой теории возмущений для изменения реактивности. Использование формулы (4.17) в расчётах изменения реактивности предполагает знание распределений
φ′(k ) (r ), J ′(k ) (r ) в возмущённом реакторе. Это приводит (как и в
100
