
КузминАМ Основы теории критичности 2008
.pdf
где функции ϕ(k ) (r ) Ωk |
и зависят лишь от переменных r , а |
||
T (t) – |
от времени t. Обозначив через λ константу разделения, |
||
придём к следующим уравнениям для функций T (t), ϕ(k ) (r ) : |
|||
|
dT (t) |
= λT (t) , |
(4.40) |
|
dt |
||
|
|
|
|
λ
υ(k )
ϕ(k ) (r ) = div(D(k ) gradϕ(k
m
+ χ(k ) ∑ν (f j)Σ(fj)ϕ( j) (r j=1
|
k −1 |
|
) (r )) − Σ(adk ) ϕ(k ) (r ) + ∑Σ(dj→k )ϕ( j) (r ) + |
||
|
j =1 |
|
) , |
k =1, 2,…, m . |
(4.41) |
Отсюда следует, что T (t) ~ exp(λt) , а константа разделения λ
может принимать лишь такие значения, при которых существуют нетривиальные решения уравнений (4.41).
Приведём систему уравнений (4.41) к привычному виду задач на собственные значения:
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λϕ (r ) = |
|
|
|
|
|
ϕ (r ) Ω, |
|
(4.42) |
|
|||||||||||
|
|
|
(υˆM )ϕ (r ) , |
|
|
|
|||||||||||||||||
где |
ϕ |
(r ) |
|
– векторная |
функция |
(с |
компонентами |
||||||||||||||||
ϕ(k ) (r ), k =1, 2,…, m ), |
|
соответствующая |
числу |
λ , |
υˆ |
– |
|||||||||||||||||
диагональная матрица с элементами υ |
(k ) |
, |
|
ˆ |
|
|
|
||||||||||||||||
|
|
|
|
M – дифференциальный |
|||||||||||||||||||
матричный |
оператор |
такой, что |
ˆ |
|
|
|
|
|
|
векторная функция |
с |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||
Mϕ – |
|
||||||||||||||||||||||
|
|
|
|
|
ˆ |
|
|
(k ) |
, |
совпадающими |
с правыми |
частями |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
компонентами (M ϕ ) |
|
||||||||||||||||||||||
уравнений (4.41) |
|
при одних и тех же индексах k. Множество Ω |
|||||||||||||||||||||||||||||||
образуют векторные функции, компоненты которых ϕ(k ) (r ) Ωk . |
|
||||||||||||||||||||||||||||||||
|
|
Введём |
в |
рассмотрение |
|
сопряжённый |
|
|
|
|
ˆ |
+ |
, |
||||||||||||||||||||
|
|
|
оператор M |
|
|||||||||||||||||||||||||||||
определённый на |
векторных |
функциях |
ϕ |
+ (r ) , принадлежащих |
|||||||||||||||||||||||||||||
такому |
множеству |
|
Ω+ , |
|
что имеет |
|
|
место |
|
равенство |
|||||||||||||||||||||||
|
|
+ |
ˆ |
|
|
ˆ + |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ϕ |
|
|
|
|
, ϕ |
для |
любой |
|
|
функции |
|
ϕ (r ) Ω . |
|||||||||||||||||||||
|
, Mϕ = M |
ϕ |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ˆ |
|
|
+ |
|
ˆ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Учитывая, что (υˆM ) |
|
= M |
υˆ , сформулируем сопряжённую задачу |
||||||||||||||||||||||||||||||
на собственные значения λ |
+ |
|
|
|
|
ˆ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ˆ |
оператора M |
υˆ : |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
+ |
|
|
|
|
|
+ |
|
|
+ |
(r ) , |
|
|
|
+ |
(r ) Ω |
+ |
|
|
|
|
|
|||
|
|
|
|
|
|
λ ϕ |
|
|
(r ) = (M |
υˆ) ϕ |
|
ϕ |
|
|
, |
|
|
|
|
||||||||||||||
111

где ϕ + (r ) – собственная функция, соответствующая числу λ+ . Для
|
|
+ (r ) =υˆ |
ϕ |
+ (r ) |
она примет вид: |
|
|
|
|||||||||||
функций ξ |
|
|
|
||||||||||||||||
+ |
|
+ |
|
|
ˆ |
+ |
|
|
+ |
(r ) , |
|
|
+ |
(r ) Ω |
+ |
|
|
||
|
|
|
)ξ |
ξ |
. |
(4.43) |
|||||||||||||
|
|
λ ξ |
|
(r ) = (υˆM |
|
|
|
|
|||||||||||
Вмногогрупповом диффузионном приближении множества Ω и
Ω+ совпадают, а уравнениям (4.43) соответствуют:
+ |
|
m |
λ |
ξ+(k ) (r ) = div(D(k ) gradξ+(k ) (r )) −Σ(adk )ξ+ |
(k ) (r ) + ∑Σ(dk → j)ξ+( j) (r ) + |
(k ) |
||
υ |
j =k +1 |
|
|
m |
|
+ν (fk )Σ(fk ) ∑χ( j)ξ+( j) (r ) , ξ+(k ) (r ) Ωk , |
k =1,2,…, m . (4.44) |
|
|
j=1 |
|
Установлено, что в общем случае задачи вида (4.42), (4.43) имеют один и тот же спектр σ (λ) собственных значений, в
котором помимо дискретного ряда чисел (действительных и комплексных) может присутствовать область непрерывного изменения λ (сплошного спектра). Однако всегда существует
ведущее собственное число λ0 , которое является действительным, изолированным и удовлетворяет неравенству:
|
|
λ0 > Reλi , |
(4.45) |
|
где λi |
– любой, не совпадающий с λ0 , элемент спектра σ (λ) . |
|||
Числу |
λ0 |
соответствуют |
единственные собственные функции |
|
ϕ0 (r ) |
(с |
компонентами |
ϕ0(k ) (r ) ) и ξ0+ (r ) |
(с компонентами |
ξ0+(k ) (r ), k =1,2,…, m ), обращающиеся в нуль лишь на внешней границе реактора.
Допустим, что спектр σ (λ) |
содержит лишь дискретный набор |
|||||
чисел |
λi (i = 0,1,2,…,m) , а |
система |
соответствующих им |
|||
собственных |
функций |
ϕi |
(r ) |
(с |
компонентами |
|
ϕi(k ) (r ) , |
k =1, 2,…, m ) полна. |
Такое предположение выполняется, |
||||
например, в многогрупповом диффузионном приближении для любой одномерной геометрии реактора с непрерывной пространственной зависимостью. В этом случае (принимая во внимание выражение (4.39)) поток нейтронов в каждой энергетической группе можно представить в виде разложения:
112

∞ |
|
φ(k ) (r ,t) = ∑Ai exp(λit)ϕi(k ) (r ) , k =1, 2,…, m . |
(4.46) |
i=0
Установим следующие свойства собственных функций и числа λ0 .
|
1. Свойство ортогональности собственных функций. |
|
|||
Запишем |
уравнения |
(4.41) |
для собственной |
функции |
|
ϕi |
(r ) = (ϕi(1) ,ϕi(2) ,…,ϕi(m) )T , соответствующей числу |
λi , а |
|||
уравнения |
(4.44) – для |
функции |
ξj+ (r ) = (ξj+(1) ,ξj+(2) ,…,ξj+(m) )T , |
||
соответствующей числу |
λj . Каждое уравнение в системе (4.41) |
||||
умножим на ξ+j (k ) (r) , проинтегрируем по r V и сложим. Каждое уравнение в системе (4.44) умножим на ϕi(k ) (r ) , проинтегрируем
по r V и сложим. Из одного образовавшегося при этом равенства вычтем другое. В результате получим:
|
m |
1 |
|
|
|
|
|
|
|
||
(λi − λj )∑∫ |
ϕi(k ) (r )ξj+(k ) (r ) dV = 0 . Отсюда следует, что |
||||||||||
υ(k ) |
|||||||||||
|
k =1 V |
(k ) |
+(k ) |
0 , λi ≠ λj |
|
|
|||||
m |
1 |
|
|
|
|||||||
∑∫ |
|
ϕi |
(r )ξj |
(r ) dV = γ |
, |
λ = λ |
|
, |
(4.47) |
||
υ(k ) |
|
||||||||||
k =1 V |
|
|
|
|
i |
|
i |
j |
|
||
где значение γi задаётся в соответствии с выбранным способом
нормировки собственных функций. В дальнейшем преобразования, которые были выполнены с уравнениями (4.41), (4.44) и привели к соотношению (4.47) будем называть процедурой перекрёстного умножения, интегрирования и вычитания.
2. Соотношение между числом λ0 и реактивностью реактора.
Применим процедуру перекрёстного умножения, интегрирования и вычитания к уравнениям (4.2), (4.44), записанным для
асимптотического потока нейтронов φ0 (r ) = (φ0(1) ,φ0(2) ,…,φ0(m) )T и собственной функции ξ0+ (r ) соответственно. В результате получим:
|
|
|
1 |
|
1 |
|
|
|
λ |
= 1 |
− |
|
|
|
|
, |
(4.48) |
К |
|
ϑ |
||||||
0 |
|
|
|
|
|
|
||
|
|
|
|
эф |
0 |
|
|
|
где ϑ0 – положительный множитель, принимающий значение:
113

|
|
|
|
m |
|
|
|
||
|
|
|
|
∑∫ |
1 |
φ0(k ) (r )ξ0+(k ) (r ) dV |
|
|
|
|
|
|
|
υ(k ) |
|
|
|
||
|
ϑ0 = |
|
|
k =1 V |
|
. |
(4.49) |
||
|
|
m |
|
|
m |
|
|||
|
|
∫∑ν(fk )Σ(fk )φ0(k ) (r ) ∑χ( j)ξ0+( j) (r ) dV |
|
||||||
|
|
V k =1 |
|
|
j =1 |
|
|
|
|
Из равенства (4.48) следует, что: |
|
|
|
||||||
если |
Кэф =1 |
(критический реактор), то λ0 |
= 0 , |
|
|||||
если |
Кэф >1 |
(надкритический реактор), то λ0 > 0 , |
(4.50) |
||||||
если |
Кэф <1 |
(подкритический реактор), то |
λ0 < 0 . |
|
|||||
Множитель ϑ0 имеет размерность времени. Его можно трактовать
как время жизни (мгновенных) нейтронов в реакторе произвольной формы.
3.Собственные функции критического реактора.
Вкритическом реакторе (где Кэф =1, λ0 = 0 ) уравнения (4.41) для
компонент ϕ0(k ) (r ) собственной функции ϕ0 (r ) совпадают по
виду с уравнениями (4.2) для асимптотических потоков φ(k ) (r ) . Решения их ищутся на одном и том же множестве функций. То же самое можно сказать в отношении функций ξ0+(k ) (r ) и φ+(k ) (r ) ,
получаемых из решения уравнений (4.44) и (4.15) соответственно. Поэтому
φ(k ) (r ) = Cϕ0(k ) (r ) , φ+(k ) (r ) = C+ ξ0+(k ) (r ) , (4.51)
где C , C+ – не равные нулю постоянные множители, выбираемые
обычно из условий нормировки. Для некритического реактора соотношения (4.51) не выполняются. В этом можно убедиться, рассматривая переход к соответствующему условно-критическому реактору. В одном случае это делается за счёт изменения числа
|
ν(k ) |
|
нейтронов деления (заменяя ν(fk ) на |
f |
), а в другом случае – за |
|
||
|
Кэф |
|
счёт изменения поглощения нейтронов (заменяя макросечения Σ(adk ) на сумму Σ(adk ) + υλ(0k ) ).
114
Коэффициенты Ai в формуле (4.46) определим, используя
начальное условие (4.38), которое запишем в виде (заменив индекс i на j):
∞
φ(k ) (r,0) = ∑Aj ϕ(jk ) j=0
(r ) , k =1, 2,…, m .
Умножим обе части |
этого равенства |
на функцию |
|
1 |
|
ξ+(k ) (r ) , |
||||||
υ(k ) |
||||||||||||
|
|
|
|
|
|
|
|
i |
||||
проинтегрируем |
по |
переменным r V и сложим. |
|
Учитывая |
||||||||
свойство ортогональности (4.47), получим: |
|
|
|
|
||||||||
|
|
1 |
m |
1 |
|
|
|
|
|
|
||
Ai = |
∑∫ |
φ(k ) (r ,0)ξi+(k ) (r ) dV , |
|
|
|
(4.52) |
||||||
γ |
υ(k ) |
|
|
|
||||||||
|
|
i |
k =1 V |
|
|
|
|
|
|
|
||
m |
|
|
|
|
|
|
|
|
|
|||
где γi = ∑∫ |
1 |
ϕi(k ) (r )ξi+(k ) (r ) dV , |
i = 0,1, 2,…. |
|
|
|
||||||
υ(k ) |
|
|
|
|||||||||
k=1 V |
|
|
|
|
|
|
|
|
|
|||
Выражение (4.46) позволяет обобщить выводы, сделанные ранее (в главе 1) на базе простой модели реактора (без отражателя, в односкоростном диффузионном приближении). Учитывая свойства (4.45) и (4.50) собственных чисел, нетрудно установить, что при
t → ∞ |
потоки |
φ(k ) (r ,t) |
стремятся к |
распределениям |
|
φ(k ) (r ,t) = A exp(λ t)ϕ(k ) (r ) . |
Потоки φ(k ) (r ,t) |
в критическом |
|||
0 |
0 |
0 |
0 |
0 |
|
реакторе ( λ0 = 0 ) не зависят от времени t, а в некритическом
реакторе (λ ≠ 0) |
меняются с периодом |
T =ϑ |
|
Кэф |
. Для |
|
− Кэф |
||||
0 |
|
0 0 |
1 |
|
расчёта ϑ0 в многогрупповом приближении имеем формулу (4.49).
Переход от начальных распределений φ0(k ) (r ) |
к асимптотическим |
|||
потокам φ0(k ) (r ,t) определяется |
близостью |
собственных чисел |
||
λ , λ и происходит за время δt ≈ |
3 |
. |
|
|
|
|
|||
0 |
1 |
λ0 −λ1 |
|
|
|
|
|
|
|
Асимптотическая ценность нейтронов
Рассмотрим критический реактор с заданными свойствами, который до момента времени t = 0 работал на постоянной
115

мощности, однозначно связанной со скоростью деления ядер W0 . Пусть значению W0 соответствуют распределения потоков нейтронов φ0(k ) (r ) и сопряжённых функций φ0+(k ) (r ) , удовлетворяющих уравнениям (4.2), (4.3), (4.15), (4.16) и
соотношениям |
(4.51). Будем считать, множители C , C+ находятся |
||||
из условий: |
|
|
|
|
|
m |
|
|
|
|
|
C ∑ ∫Σ(fl)ϕ0(l ) (r′) d r′ =W0 , |
C C+ =W0 , |
(4.53) |
|||
l =1 r ′ V |
|
|
|||
а собственные |
|
|
|
|
|
функции ϕi (r ), ξi |
(r ) |
нормированы так, что в |
|||
соотношениях |
(4.47) γi =1 (i = 0,1,…) . Тогда потоки |
φ0(k ) (r ) |
|||
будут иметь размерность см−2 с−1 , функции φ0+(k ) (r ) – размерность
с−1 (если скорость нейтронов брать в см сек−1 , сечения деления –
всм−1 , а объём – в см3 ).
Предположим, что в момент времени t = 0 в единичный объём,
находящийся в окрестности точки r ′, поместили |
q(s) нейтронов |
s-й группы. Распределения нейтронов φ(k ) (r ,t) |
при t > 0 даёт |
решение уравнений (4.2) с начальным условием: |
|
φ(k ) (r ,0) =φ0(k ) (r ) +
1,
где η(k − s) = 0,
q(s)υ(s)δ(r − r ′)η(k −
k = s
k ≠ s , а δ (r − r′)
s) , r V , k =1, 2,…m , (4.54)
– дельта-функция Дирака.
Такое решение было получено ранее и записано в виде разложения (4.46). При этом коэффициенты Ai рассчитываются по формулам (4.52), в которых вместо функции φ(r ,0) берётся сумма (4.54).
116
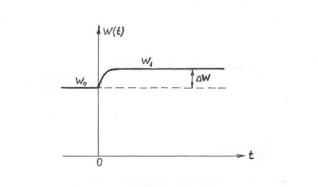
Рис.4.2. Изменение мощности W (t) со временем t
при помещении q(s) нейтронов при t = 0
По истечении некоторого промежутка времени в реакторе установится новое распределение потоков φ1(k ) (r ) , которому
соответствует новое |
значение |
мощности |
W1 =W0 + |
W (также |
|||||||||||||||
измеряемое скоростью деления ядер). Причём, |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
m |
|
1 |
ξ0+(k ) (r )φ(k ) (r ,0) d r . |
|||
φ1(k ) (r ) = φ(k ) (r ,t → ∞) = A0 ϕ0(k ) (r ), |
A0 = |
|
∑ ∫ |
||||||||||||||||
γ |
υ(k ) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
k=1 r V |
|
|
||||
Используя выражение (4.54) |
для |
потоков φ(k ) (r,0) , |
а также |
||||||||||||||||
выбранное выше |
условие |
|
нормировки |
собственных |
функций |
||||||||||||||
(γ0 |
=1) и соотношения (4.53), получим: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
A0 = C + q(s)ξ0+(s) (r′), |
|
|
W1 = ∑ ∫Σ(fk )φ1(k ) (r ) dr =W0 + q(s)φ0+(s) (r′) . |
||||||||||||||||
|
|
|
|
|
|
|
k =1 r V |
|
|
|
|
|
|
|
|
|
|
||
|
|
+(s) |
|
′ |
|
W |
|
|
|
|
|
|
|
|
|
|
|||
Отсюда следует: |
φ0 |
|
(r ) = |
|
|
, |
|
|
|
|
|
|
|
(4.55) |
|||||
|
|
q(s) |
|
|
|
|
|
|
|
||||||||||
где |
W =W1 −W0 |
– |
изменение |
асимптотической |
мощности |
||||||||||||||
реактора. Очевидно, изменение |
|
W > 0 . При ином (чем в (4.53)) |
|||||||||||||||||
выборе величины С0+ |
|
необходимо |
|
говорить |
лишь о |
||||||||||||||
пропорциональности: φ |
+(s) ~ |
|
W |
|
. |
|
|
|
|
|
|
|
|
||||||
|
q(s) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
117
Поскольку значения s и r ′ были выбраны произвольно, то полученный в виде (4.55) результат относится к любой группе k и точке r . Таким образом, значение сопряжённой функции φ0+(k ) (r )
в критическом реакторе равно (или пропорционально) тому изменению асимптотической мощности реактора, которое происходит при помещении одного нейтрона, имеющего
кинетическую энергию E(k ) = 1 mn (υ(k ) )2 |
, |
в единичный объём в |
2 |
|
φ0+(k ) (r ) получила |
окрестности точки r . Поэтому функция |
||
название ценности нейтронов группы k |
в точке r реактора по |
|
отношению к асимптотической мощности или асимптотической
ценности нейтронов. |
|
|
|
|
|
Из |
сказанного |
выше |
следует, |
что |
ценность |
φ0+(k ) (r ) ≥ 0, k =1, 2,…m |
во |
всех точках |
r V (обращается в |
||
нyль лишь на экстраполированной границе), а величина G+f ,
определяемая выражением (4.19), имеет смысл ценности нейтронов деления. При внесении в реактор дополнительного источника
нейтронов δ q(k ) (r ) , распределённого непрерывно по объёму V для
каждой группы k, полное изменение мощности |
Wq можно |
оценить по формуле: |
|
m |
|
Wq = ∑∫φ+(k ) (r )δq(k ) (r ) dV , |
(4.56) |
k =1 V |
|
если константы С0 , С0+ получены из выражений (4.53) и принято, что γ0 =1 (см. формулу (4.47)) .
Кроме того, имеет место следующий закон сохранения асимптотической ценности:
«Ценность первоначально помещённых в реактор δq нейтронов равна сумме ценностей вторичных нейтронов, появившихся за малый промежуток времени t из δq впущенных нейтронов».
Здесь вторичными нейтронами называют как возникшие в результате рассеяния и деления ядер нейтроны, так и те из δq нейтронов, которые не испытали столкновений с ядрами среды за
118
время t . В приложении 2 дано применение этого закона
сохранения к получению интегро-дифференциального уравнения для ценности нейтронов.
Теперь можно дать простое объяснение изображённым на рис.4.1 зависимостям сопряжённых функций φ+(k ) (r), k =1,2 (4.36). Учитывая, что φ+(1) (r) – ценность быстрого, а φ+(2) (r) –
ценность теплового нейтрона на расстоянии r от центра реактора, имеем:
-ценность φ+(2) (r) почти во всей активной зоне больше ценности φ+(1) (r) из-за того, что тепловые нейтроны при
столкновении с ядрами топлива имеют большую вероятность вызвать деление этих ядер, чем быстрые нейтроны;
-ценность любого нейтрона в отражателе меньше ценности того же нейтрона в активной зоне, поскольку помещаемый в отражатель нейтрон может привести к изменению мощности реактора лишь в том случае, если он в результате диффузии попадёт в активную зону; однако этому препятствуют процессы поглощения нейтрона в отражателе и утечки его из реактора;
-ценности нейтронов φ+(k ) (r), k =1, 2 по мере удаления от
центра активной зоны непрерывно уменьшаются сначала (при приближении r к радиусу активной зоны R) за счёт возрастания вероятности утечки нейтронов в отражатель, а затем (при удалении r от R) – за счёт уменьшения вероятности нейтронам вернуться в активную зону.
Взаключение отметим, что понятие асимптотической ценности нейтронов и закон сохранения ценности можно распространить на некритические состояния реактора. В этом случае необходимо рассматривать условно-критический реактор, отличающийся от реально существующего лишь тем, что в нём при одном делении
любого ядра появляется |
ν f |
нейтронов. Как известно, в таком |
|
||
|
Кэф |
|
реакторе существует стационарное распределение нейтронов, и
119
можно говорить об асимптотической мощности и её изменении при помещении дополнительного числа нейтронов.
4.5. Применения соотношений теории возмущений
Соотношения (4.18), (4.19) позволяют оценить изменение реактивности (при известных значениях δ Σ(trk ) , δ Σ(adk ) и т.д.),
используя решения лишь двух примерно одинаковых по вычислительным затратам задач (4.2) – (4.4) и (4.10), (4.15), (4.16),
сформулированных для невозмущённого реактора. Время счёта при этом практически не зависит от числа возмущаемых параметров. Единственное требование состоит в том, чтобы каждое из возмущений было мало. В противном случае расчёты по формулам (4.18), (4.19) могут привести к заметным погрешностям в
определении δ Кэф .
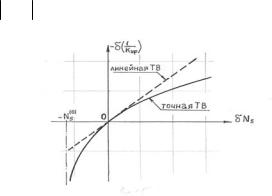
Это иллюстрирует рис.4.3, на котором представлены
|
1 |
|
|
|
|
зависимости −δ |
|
|
от изменения |
δ N5 |
концентрации U-235 в |
|
|||||
|
Кэф |
|
|
|
|
активной зоне реактора (через N5(0) обозначена концентрация
урана-235 в невозмущённом реакторе). Видно, что совпадение результатов расчёта по точной формуле (4.17) и формуле теории малых возмущений (4.18) имеет место в том случае, когда
величина δ N5 мала.
Рис.4.3. Сравнение результатов расчёта по формулам (4.17) и (4.18)
120
