
КузминАМ Основы теории критичности 2008
.pdf
случае разностного метода нахождения δКэф ) к большому объёму
вычислений, когда рассматривается много различных возмущений. Можно существенно сократить вычисления, если предположить, что возмущения малы, а решение задачи (4.7) - (4.9) меняется
непрерывно с изменением δu , т.е. отклонения δКэф , δφ(k ) , δJ (k ) ,
δΣtr(k ) ,δΣ(adk ) ,δΣ(dj→k ) ,δ(ν(fk )Σ(fk ) ),δu являются величинами одного
итого же порядка малости. При этом речь идёт об изменении нормированного асимптотического потока в любой части реактора.
′(k ) |
|
Заменим |
в равенстве |
(4.17) |
возмущённые значения |
||||
′(k ) |
, φ |
′(k ) |
, J |
′(k ) |
суммами |
(4.5), |
(4.6). Ограничиваясь |
||
ν f |
Σf |
|
|
|
|||||
слагаемыми первого порядка малости Ο(δu ) , получим:
δКэф |
m |
m |
|
G+f = ∑∫3δΣtr(k ) (J +(k ) (r ), J (k ) (r ))dV − ∑∫φ+(k ) (r )δΣ(adk )φ |
|||
2 |
|||
Кэф |
k =1 V |
k =1 V |
|
mk−1
+∑∫φ+(k ) (r )∑δΣ(dj→k )φ(k ) (r )dV +
|
|
k=1 V |
j=1 |
|
|
1 |
m |
m |
|
+ |
∑χ(k )φ+(k ) (r )∑δ(ν (fl )Σ(fl ) )φ(l ) (r ) dV , |
|||
|
||||
|
Кэф V∫k =1 |
l=1 |
||
|
|
m |
m |
|
где |
G+f |
= ∫∑χ(k )φ+(k ) (r )∑ν(fl )Σ(fl )φ(l ) (r )dV , |
||
|
|
V k =1 |
l =1 |
|
(k ) (r )dV +
(4.18)
(4.19)
|
1 |
|
|
δКэф |
|
и принято, что в рассматриваемом случае δ |
|
|
= − |
|
. |
|
2 |
||||
|
|
|
|
|
|
|
Кэф |
|
Кэф |
|
|
Соотношение (4.18) называют формулой теории малых возмущений. Она позволяет ограничиться решением всего лишь двух задач (4.2) - (4.4) и (4.10), (4.15), (4.16), сформулированных для невозмущённого реактора. Не требуется находить распределения нейтронов в возмущённых реакторах. За счёт этого удаётся заметно снизить вычислительные затраты по сравнению с теми, которые делаются при использовании точной формулы (4.17). Однако соотношением (4.18) можно пользоваться лишь в том случае, когда возмущение реактора мало. При этом должно
101

быть близко к нулю не только значение δКэф , но и отклонения
δφ(k ) (r ) при любых r V , k =1, 2,…, m .
4.2. Итерационный метод решения
Получение распределений φ(k ) (r ) , φ+(k ) (r ) связано с
рассмотрением двух задач на собственные значения: решением системы однородных уравнений (4.2), (4.3) или (4.15), (4.16) при условиях (4.4) или (4.10), включающих обращение в нуль искомых функций на внешней (экстраполированной) границе реактора. Известно, что эти задачи имеют одинаковый спектр собственных
значений, состоящий лишь из отдельных чисел k0 , k1 ,…. Самое большое (по модулю) число k0 = max( k0 , k1 ,…) является
действительным, положительным и имеет смысл эффективного коэффициента размножения нейтронов Кэф . Ему соответствует
единственное решение: векторная функция ψ0 (r ) с компонентами
ψ0(k ) (r ) в задаче (4.2) – (4.4) и векторная компонентами ψ0+(k ) (r ) в задаче (4.15),
функция ψ0+ (r ) с (4.16). Поскольку
собственные функции определены с точностью до постоянных множителей, то можно считать, что
φ(k ) (r ) =ψ0(k ) (r ) , φ+(k ) (r ) =ψ0+(k ) (r ) .
Для нахождения собственных функций, соответствующих максимальному числу k0 = Кэф , используется метод итераций
источника. Ранее (в разделе 1) для реактора без отражателя в односкоростном диффузионном приближении была
продемонстрирована сходимость метода к функции ψ0 (r ) .
Обоснование сходимости метода в общем случае дано в работе [3]. В главе 3 изложен алгоритм метода для определения асимптотических потоков φ(k ) (r ) в многогрупповом
диффузионном приближении. При решении сопряжённых уравнений (4.15), (4.16) он выглядит следующим образом.
102

На каждой n-й итерации последовательно, начиная с последней энергетической группы нейтронов m , решаются уравнения:
− div (D(k ) gradφn+(k ) (r )) + Σ(adk ) φn+(k ) (r ) =ν (fk )Σ(fk ) |
fn+−1(r ) + |
m |
|
+ ∑Σ(dk→ j ) φn+( j) (r ) , k = m, m −1, m − 2,…1 , |
(4.20) |
j=k+1 |
|
где fn+−1(r ) – источник, который на 1-й итерации задаётся в виде
не равной тождественно нулю положительной функции, а на следующих итерациях рассчитывается по формуле:
m
fn+ (r ) = ∑χ(k )φn+(k ) (r ) , n =1, 2,…
k=1
Каждое из уравнений (4.20) при известной правой части имеет вид односкоростного уравнения диффузии с источником и решается при условиях (4.10), обычно, численным методом.
Итерации прекращаются при таком n=N, когда впервые при заданной погрешности ε > 0 выполнится неравенство:
Кэф(n) − Кэф(n−1) ≤ ε Кэф(n) ,
∫ fn+ (r )dV
где К(n) = |
V |
|
- |
приближённое |
значение |
|
∫ |
|
|||||
эф |
fn+−1 (r )dV |
|
|
|
||
итерации. |
V |
Полученные |
таким |
образом |
||
|
||||||
Кэф = Кэф( N ) , |
φ+(k ) (r ) =φN+(k ) (r ) |
принимаются |
||||
решения уравнений (4.15), (4.16). |
|
|
||||
Кэф на n-й
значения
вкачестве
4.3. Сопряжённые уравнения для простых моделей реактора
Односкоростное приближение. В этом приближении вероятности взаимодействий нейтронов с ядрами среды не зависят от энергии нейтронов. Поэтому рассматривается только одна
группа нейтронов и принимается, что φ(1) (r ) =φ(r ) и
φ+(1) (r ) =φ+ (r ) .
Асимптотический поток нейтронов φ(r ) и сопряжённая функция φ+ (r ) являются решениями одинаковых уравнений:
103

div(D grad φ(r ))−Σa φ(r ) + К1эф ν f Σf φ(r ) = 0 ,
div (Dgrad φ+ (r ))−Σa φ+ (r ) + |
1 |
ν f Σ f φ+ (r ) = 0 |
(4.21) |
|
|||
|
Кэф |
|
|
и принадлежат одному и тому же множеству функций. Поэтому
φ+ (r ) = Cφ(r ) ,
где множитель С может принимать любое не равное нулю значение. В результате выражение (4.18) преобразуется к виду:
|
δКэф |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= |
|
|
3δΣ |
|
D |
|
grad φ(r ) |
|
− δΣ |
|
φ |
|
(r ) + |
|
δ (ν |
|
Σ |
|
)φ |
|
(r ) dV , |
|
Кэф2 |
G+f V∫ |
tr |
|
|
a |
|
Кэф |
f |
f |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где G+f |
= ∫ν f Σf |
φ2 (r ) dV . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.22) |
|||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Реактор без отражателя. Пусть реактор без отражателя состоит из одной однородной активной зоны и имеет единую для всех групп нейтронов экстраполированную границу. Тогда можно, воспользовавшись методом разделения переменных, искать
распределения φ(k ) (r ), φ+(k ) (r ) в виде:
φ(k ) (r ) = I0(k ) ψ0 (r ) , φ+(k ) (r ) = I0+(k ) ψ0 (r ) , |
(4.23) |
где ψ0 (r ) – собственная функция, соответствующая ведущему собственному числу α02 (называемому также геометрическим параметром реактора) задачи:
|
ψ |
0 |
(r ) + α2 ψ |
0 |
(r ) = 0, |
|
ψ |
0 |
(r ) = 0 , |
(4.24) |
|
|
|
|
0 |
|
|
|
э |
|
|||
а |
I0(k ) , I0+(k ) (k =1, 2,…, m) |
– |
|
неизвестные |
множители, |
||||||
независящие от пространственной переменной r . |
|
||||||||||
|
Подставляя в |
уравнения (4.2), |
(4.3) |
и (4.15), |
(4.16) вместо |
||||||
φ(k ) (r ), φ+(k ) (r ) |
выражения (4.23) |
и учитывая равенство (4.24), |
|||||||||
получим алгебраические уравнения для определения множителей I0(k ) , I0+(k ) . При этом уравнения и алгоритм расчёта амплитуд I0(k )
ничем не отличается от приведённых в разделе 3.4 (см. формулы
(3.57) – (3.59)).
Для нахождения I0+(k ) имеем однородную систему уравнений:
104
m |
1 |
m |
|
−α02 D(k ) I0+(k ) −Σ(adk ) I0+(k ) + ∑ Σ(dk→ j) I0+( j) + |
ν (fk ) Σ(fk ) ∑χ(l) I0+( j) = 0 , |
||
Кэф |
|||
j=k+1 |
l=1 |
||
k =1, 2,…, m , |
|
(4.25) |
решение которой нетрудно получить, воспользовавшись нормировкой:
m |
|
Кэф = ∑χ( j) I0+( j) . |
(4.26) |
j=1
Врезультате придём к простым формулам расчёта I0+(k ) (начиная
со значения I0+(m) для последней группы):
m
ν (fk )Σ(fk ) + ∑Σ(dk→ j ) I0+( j )
I +(k ) |
= |
|
j=k+1 |
, k = m, m −1,…,1 . |
|
α02 D(k ) +Σ(adk ) |
|||
0 |
|
|
|
|
Величину |
Кэф |
(при известных значениях I0(k ) , I0+(k ) ) получим с |
||
помощью формул (3.58) или (4.26).
Представление решений уравнений (4.2), (4.3) и (4.15), (4.16) в форме (4.23) позволяет изменение δКэф , обусловленное малым
изменением свойств реактора в пределах объёма V0 V , записать в виде:
δКэф = δtr K +δc K +δd K +δ f K , |
(4.27) |
где отдельные слагаемые отвечают за изменения соответствующих макроскопических сечений и рассчитываются по формулам:
m
δtr K = 3∑δΣ(trk ) (D(k )
k=1 |
|
m−1 |
m |
δd K = ∑I0(k ) ∑δΣ(dk |
|
k=1 |
j=k+1 |
|
|
|
m |
)2 I0(k ) I0+(k ) ξ0 , |
δc K = −∑δΣ(ck ) |
||
|
|
|
k=1 |
→ j) (I +( j) − I +(k ) )ξ |
, |
||
0 |
0 |
1 |
|
δ f K = ∑m [δ(ν (fk )Σ(fk ) ) I0(k ) −δΣ(fk ) I0(k ) I0+(k ) ]ξ1 . k=1
I0(k ) I0+(k ) ξ1 ,
(4.28)
105
|
|
∫ |
|
gradψ0 (r ) |
|
2 dV |
|
∫ψ02 (r ) dV |
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
Здесь |
ξ0 = |
V0 |
|
|
|
|
, |
ξ1 = |
V0 |
|
и принято |
||
|
|
∫ψ02 (r ) dV |
|
∫ψ02 (r ) dV |
|||||||||
|
|
|
|
V |
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
во |
внимание, |
что |
Σ(dk ) |
= ∑Σ(dk→ j ) , |
а |
поэтому |
|||||||
|
|
|
|
|
|
|
|
|
|
j=k +1 |
|
|
|
m |
k−1 |
|
|
|
m−1 |
|
m |
|
|
|
|
||
∑I0+(k ) ∑δΣ(dj→k ) I0( j ) = ∑I0(k ) ∑δΣ(dk→ j) I0+( j) . |
|
|
|||||||||||
k=2 |
j=1 |
|
|
|
k=1 |
j=k+1 |
|
|
|
|
|||
Двухгрупповые уравнения диффузионно-возрастного приближения. В этом приближении рассматривается 2-е группы нейтронов: замедляющиеся (или быстрые) и тепловые нейтроны. Основные допущения перечислены в разделе 3.1 пособия, а
уравнения для потоков быстрых φ(1) (r ) и тепловых φ(2) (r ) приведены в разделе 3.3 той же главы. В том же приближении
получим |
следующие сопряжённые |
уравнения для функций |
||
φ+(1) (r ), |
φ+(2) (r ) : |
|
|
|
div(D(1) grad φ+(1) (r ))− Σ(ad1) φ+(1) (r ) + Σ(d1→2)φ+(2) (r ) = 0 , |
||||
div(D(2) grad φ+(2) (r ))− Σ(a2) φ+(2) (r ) + |
μ |
ν (f |
2)Σ(f2) φ+(1) (r ) = 0 . |
|
|
||||
|
|
Кэф |
|
|
Если воспользоваться выражениями (3.46), (3.47) для макроскопических сечений, то их можно записать в виде:
φ+(1) (r ) − 1 |
φ+(1) |
(r ) = − |
ϕ φ+(2) |
(r ) , |
|||
|
τ |
|
|
τ |
(4.29) |
||
|
1 |
|
|
|
~ |
|
|
φ+(2) (r ) − |
φ+(2) |
(r ) = − |
K∞ |
φ+(1) (r ). |
|||
2 |
2 |
||||||
|
L |
|
|
ϕL |
|
||
Сопряжённые уравнения (4.29), как и уравнения (3.61), (3.62) для потоков нейтронов φ(1) (r ), φ(2) (r ) , приводятся к виду (3.63). Вследствие этого их решения строятся на базе одних и тех же функций ψ1(r ),ψ2 (r ) , удовлетворяющих уравнениям (3.67) при значениях ω1, ω2 , определяемых выражениями (3.66). Поэтому имеем:
106
φ+(1) (r ) = A+(1)ψ |
(r ) + A+(1)ψ |
2 |
(r ) , |
|
|
||||||
1 |
1 |
|
|
2 |
|
|
|
|
(4.30) |
||
φ+(2) (r ) = A+(2)ψ |
|
(r ) + A+(2)ψ |
|
|
(r ). |
|
|||||
|
2 |
|
|
||||||||
1 |
1 |
|
2 |
|
|
|
|
|
|||
Но теперь для коэффициентов |
A+(1) |
, A+(2) , A+(1) |
, A+(2) |
получим, |
|||||||
|
|
|
|
1 |
|
1 |
|
|
2 |
2 |
|
используя уравнения (4.29), соотношения:
|
A+(2) = p+ A+(1) |
, |
|
|
1 |
1 |
|
где |
p+ = |
τc (1 +ω1τ) |
, |
|
|
ϕτ |
|
+(1) |
|
|
|
~+ |
+(2) |
, |
|
(4.31) |
|
A2 |
|
= p |
A2 |
|
|||||
~+ |
|
|
|
|
ϕτ |
|
|
|
|
p |
= |
|
|
|
|
. |
|
||
τ |
c |
(1 +ω τ) |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
Если ограничиться рассмотрением одномерной геометрии реактора, а линейно-независимые решения уравнений (3.67) обозначить так же, как в разделе 3.5, то для i -й зоны реактора выражения (4.30) примут вид:
- в случае |
|
активной |
зоны |
(когда |
|
|
~(i) |
>1+εi , а |
параметры |
||||||||||||||
|
|
|
K∞ |
|
|||||||||||||||||||
принимают |
|
значения |
ω = β |
2 , |
ω |
2 |
= −γ |
2 |
, |
определяемые по |
|||||||||||||
формулам (3.66)): |
|
1 |
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|||||||
|
|
|
~+ |
|
|
~ |
|
|
|
|
|
+ ~ |
|
|
|
||||||||
+(1) |
|
|
+ |
|
|
+ |
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||
φi |
(r) = ai |
f (βi r) +bi |
g(βi r) + pi |
[ci |
|
f |
(γi r) + di |
g(γi r)]; |
(4.32) |
||||||||||||||
+(2) |
|
|
+ |
|
+ |
|
+ |
|
|
+ |
~ |
|
|
|
|
|
+ ~ |
||||||
φi |
(r) = pi |
[ai f (βi r) +bi g(βi r)]+ ci |
|
|
f (γi r) |
+ di g(γir); |
|
|
|
||||||||||||||
|
|
|
|
|
~(i) |
|
|
|
2 |
|
|
|
|
1 |
|
|
|
2 |
1 |
|
|||
- в отражателе (где K∞ |
|
= 0, ω1 = −υi |
|
= − |
|
|
|
, |
ω2 |
= −ϑi = − |
|
): |
|||||||||||
|
|
τ |
i |
|
L2 |
||||||||||||||||||
|
|
|
|
|
~ |
|
+ ~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
+(2) |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.33) |
||||||
φi |
|
(r) = ci |
|
f (ϑir) + di g(ϑir) ; |
|
|
|
|
~ |
|
|
|
|
|
+ ~ |
||||||||
+(1) |
|
|
+ |
~ |
|
+ ~ |
|
~+ |
|
|
+ |
|
|
|
|
|
|
|
|
||||
φi |
|
(r) = ai |
|
f (υir) +bi g(υir) + pi [ci |
f (ϑir) + di g(ϑir)]. |
|
|||||||||||||||||
Здесь: a+ , |
b+ , c+ , d |
+ |
– множители, |
выбираемые |
так, |
чтобы |
|||||||||||||||||
|
|
i |
|
i |
i |
i |
|
|
|
|
|
|
~+ |
|
|
|
|
|
|
|
|
||
выполнялись |
|
условия |
|
(4.10), |
а |
|
+ |
|
|
|
– |
коэффициенты |
связи |
||||||||||
|
|
pi , |
|
pi |
|
|
|||||||||||||||||
(4.31), рассчитываемые по свойствам i -й зоны.
Для каждой геометрии выражения (4.32), (4.33) принимают определённый вид. Как и при нахождении потоков нейтронов, выполнение граничных условий приведёт к исключению некоторых частных решений (путём приравнивания нулю стоящих перед ними множителей). Например, для реактора с одной
активной зоной (которой соответствует i =1) в сферически симметричной геометрии:
107
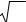
φ+(1) |
(r) = a+ |
sin(β1r) |
, |
φ+(2) |
(r) = a+ p+ |
sin(β1r) |
. |
(4.34) |
β r |
|
|||||||
1 |
1 |
|
1 |
1 1 β r |
|
|||
|
|
1 |
|
|
1 |
|
|
|
Таким образом, сопряжённые функции (как и потоки нейтронов в реакторе без отражателя) имеют одну и ту же зависимость от пространственной координаты r . При этом:
φ+(2) |
(r) |
+ |
(1+ε |
)(1+ β2τ) |
|
|
1 |
|
= p1 = |
1 |
1 |
. |
(4.35) |
φ+(1) |
(r) |
|
ϕ |
|||
1 |
|
|
|
|
|
|
Поскольку в тепловом реакторе с резонансным поглотителем вероятность ϕ <1, а значение ε1 обычно близко к нулю, то в
активной зоне p1+ >1 и, следовательно, выполняется неравенство:
φ1+(2) (r) >φ1+(1) (r) .
Если активная зона (i =1) радиуса R окружена бесконечным отражателем (i = 2) , то в той же геометрии:
|
+(1) |
+ |
sin (β r) |
|
+ |
~ |
+ |
+ sh(γ r) |
|||||||||||||
|
|
|
(r) = a1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
||||
φ1 |
|
|
|
|
− p1 |
p1 |
η1 |
|
|
|
|
|
|
||||||||
|
|
|
β r |
|
|
γ |
1 |
r |
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
φ |
+ |
(2) |
(r) = a |
+ |
p |
+ sin (β r) |
− |
η |
+ |
sh(γ r) |
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
β r |
|
|
γ |
|
r |
|
|
||||||||||
1 |
|
1 |
1 |
|
1 |
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
при 0 ≤ r ≤ R ,
при 0 ≤ r ≤ R ,
+(2) |
|
|
+(2) |
|
|
|
|
R |
|
|
|
|
|
|
|
r − R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(r) = |
(R) |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
φ2 |
|
φ1 |
|
|
exp |
|
|
|
|
при |
r ≥ R , |
|
|
(4.36) |
|||||||||||||||||||||
|
|
r |
L |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+(1) |
|
|
+(1) |
|
|
|
|
~+ |
+(2) |
|
|
R |
|
|
|
|
r |
− R |
|
|
|
|||||||||||||
φ2 |
(r) = [φ1 |
|
|
(R) − p2 φ1 |
|
|
(r)] |
|
|
exp |
− |
|
|
|
|
|
|
|
+ |
|
|
|
|||||||||||||
|
|
|
|
r |
|
|
|
τ |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~+ +(2) |
|
|
|
|
R |
|
|
|
|
r − R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
+ p2 |
φ1 |
(R) |
|
|
|
exp |
− |
|
|
|
|
|
при r ≥ R , |
|
|||||||||||||||||
|
|
|
|
|
r |
|
|
L |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
где |
+ |
|
γ1 |
sin(β1R) + β1 L2 cos(β1R) |
|
|
+ ~+ |
|
|
1+ β12τ1 |
< 0 . |
||||||||||||||||||||||||
η1 |
= |
|
sh(γ |
|
R) + |
γ |
|
L ch(γ |
R) |
, |
p1 |
p1 |
|
= |
|
|
|
|
|||||||||||||||||
β |
1 |
1 |
|
|
1−γ 2τ |
1 |
|
||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||
108

Рис.4.1. Распределения φ+(1) (r) и φ+(2) (r) в реакторе с отражателем
При получении соотношений (4.36) принято, что D1(2) = D2(2) ;
коэффициенты b1+ = b2+ = d1+ = d2+ = 0 (чтобы выполнялись условия (4.10) в центре реактора и на бесконечности), а коэффициенты
c+, a+, c+ |
|
выражены через значение a+ с помощью условий: |
|||||||||||||||
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
φ+(1) |
(R) =φ+(1) |
(R), |
|
|
|
φ+(2) |
(R) =φ+(2) (R) , |
|
||||||||
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
||||
|
|
|
|
D(2) |
dφ+(2) |
|
|
= D(2) |
dφ+(2) |
|
. |
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
2 |
|
|
||||||
|
|
|
1 |
dr |
|
|
r =R |
2 |
|
dr |
|
r =R |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, |
|
|
в |
этом |
|
|
|
случае |
|
выполнение |
равенства |
||||||
D(1) |
dφ+(1) |
|
= D(1) |
dφ+(1) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
2 |
|
|
|
даёт условие критичности реактора, |
||||||||||
|
|
|
|
||||||||||||||
1 |
dr |
|
|
|
2 |
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
r =R |
|
|
|
|
|
|
r =R |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
которое имеет такой же вид, как в задаче нахождения распределений нейтронов.
Как и в разделе 3.5, можно установить, что |
0 <η+ <<1. |
|
1 |
Поэтому последние слагаемые в выражениях (4.36) для функций φ1+(1) (r), φ1+(2) (r) вносят заметный вклад в соответствующие
суммы лишь вблизи границы r = R . Вдали же от неё (как и в реакторе без отражателя) достаточно хорошо выполняются
109

соотношения (4.34), (4.35). В отражателе функция φ2+(2) (r)
непрерывно уменьшается с ростом r . Таким образом, зависимость её от пространственной координаты может заметно отличаться от
потока тепловых нейтронов φ2(2) (r) , который (как это установлено
ранее) может иметь «всплеск» в отражателе. Эти особенности сопряжённых функций отражены на рис.4.1.
4.4. Физический смысл сопряжённой функции
Для выяснения физического смысла |
функций φ+(k ) (r ) |
рассмотрим вначале особенности решения нестационарных уравнений для потоков нейтронов φ(k ) (r ,t) в многогрупповом
диффузионном приближении (без учёта запаздывающих нейтронов, с неменяющимися со временем сечениями):
1 ∂φ(k ) (r,t)
υ(k ) ∂t
k−1
+∑Σ(dj→k ) φ( j) j=1
= div(D(k ) gradφ(k ) (r,t)) −Σ(adk )φ(k ) (r,t) +
m |
|
(r,t) + χ(k ) ∑ν (f j)Σ(fj)φ( j) (r,t), |
k =1, 2,…, m , |
j=1 |
|
(4.37)
при условиях:
φ(k ) (r,t) |
|
t=0 |
=φ(k ) (r,0) , |
φ(k ) (r,t) Ω |
k |
. |
(4.38) |
|
|||||||
|
|
|
|
|
|
||
Здесь υ(k ) |
– средняя |
скорость нейтронов |
k-й группы, |
||||
макроскопические сечения не зависят от времени t, а множества Ωk описываются соотношениями (4.4).
Свойства решений нестационарной задачи
Будем искать решение нестационарной задачи (4.37), (4.38) методом разделения переменных, представив потоки φ(k ) (r ,t) в
виде: |
|
φ(k ) (r,t) =T (t)ϕ(k ) (r ), k =1,2,…,m , |
(4.39) |
110
