КузминАМ Основы теории критичности 2008

Таким образом, решение двумерного уравнения (П.1.1) заменяется решением системы из четырёх (по числу слоёв в реакторе) одномерных уравнений (П.1.6) - (П.1.9). Однако эта система оказывается нелинейной из-за зависимости параметров

γi, j (H j ), αi, j (Ri ) от искомых функций. Поэтому используется

итерационный метод, в котором последовательно решаются две задачи: задача «А» – решение уравнений (П.1.6), (П.1.7) при

условиях (П.1.12) для функций ϕi, j (r) , описывающих радиальные распределения в слоях j = 1, 2, и задача «В» – решение уравнений (П.1.8), (П.1.9) при условиях (П.1.13) для функций ξi, j (z) ,

описывающих аксиальные распределения в слоях i = 1,2 . На

каждой n-й итерации выполняются следующие вычисления.

По заданным (на первой итерации) или полученным из предыдущей итерации (при n=2, 3, …) значениям γi, j (H j ) = γi(,nj−1)

решается задача «А», находятся распределения ϕi, j (r) =ϕi(,nj) (r) ,

наименьшее собственное число α1(,n1) и оценивается эффективный коэффициент размножения нейтронов Кэф = КА(n) из равенства:

141

определения по формулам (П.1.10) параметров αi, j (Ri ) . При этом

используются при решении задачи «В». В результате определяется наименьшее собственное число γ задачи, соответствующие ему

распределения ξi(,nj) (z) и оценивается значение Kэф = KB(n) из соотношения:

рассчитываются параметры γi, j (H j ) . Причём, как и в задаче «А» (но только интегрированием уравнения (П.1.8) по z H1 ), можно установить, что γ1,1(H1) = γ . На этом заканчивается одна

итерация.

Итерационный счёт продолжается до тех пор, пока не перестанут меняться (в пределах заданных погрешностей) значения

αi(,nj) ,γi(,nj) , K , K . Если это произойдёт, начиная с итерации

n=N, то в качестве эффективного коэффициента размножения двумерного реактора принимается:

Kэф = K A( N ) или Kэф = KB( N ) ,

а собственные функции ϕ ( N ) (r), ξ ( N ) (z) используются для оценки двумерного распределения ψ0 (r, z) .

142

~

а fi,2 (r) – какое-либо частное решение неоднородного уравнения.

Подставляя сумму (П.1.17) в уравнение (П.1.7) и учитывая равенства (П.1.6) и (П.1.18), получим:

Реактору с активной зоной, окружённой отражателем, можно сопоставить эквивалентный «голый» (без отражателя) реактор, в

котором материальный ω (2.1) и геометрические αr2 , αz2 (2.14) параметры равны:

то решение задачи о критичности эквивалентного реактора при условиях

даст те же значения Кэф и асимптотического потока нейтронов

φ(r, z) , что и полученные выше в приближении (П.1.4) в активной

зоне реактора с отражателем.

МУРП может быть использован для приближённого расчёта потока нейтронов в более сложных моделях реакторов. Например, если рассматривается многозонный реактор с m слоями в аксиальном и n слоями в радиальном направлениях, а асимптотический поток нейтронов ищется в односкоростном диффузионном приближении, то придём к следующим двум системам одномерных уравнений.

Для функций ϕi, j (r) , описывающих радиальные распределения нейтронов в зонах j -х аксиальных слоёв, получим уравнения:

144

Для функций ξi, j (z) , описывающих аксиальные распределения

(П.1.22)

В случае, когда рассматривается многозонный реактор в цилиндрической геометрии, а потоки φ(k ) (r, z) в энергетических группах k =1,2,…, m находятся из решения уравнений (3.32), (3.36), основное допущение метода формулируется в виде:

145

(номера диапазонов возрастают с уменьшением энергии нейтронов

распределение.

Ограничимся рассмотрением одномерной модели реактора, состоящего из n зон разного состава (рис.2.1). В этом случае

имеем один аксиальный слой, в котором ζi(,1g ) = cos(αz z) , где αz2 - геометрический параметр, рассчитываемый по формуле (2.14).

(П.1.23), придём к следующим уравнениям для функций ϕi( g ) (r) :

146

где макроскопические сечения (средние в диапазоне g ) находятся по формулам:

принятых для потоков φ(k ) (r) , и получаются путём суммирования

соответствующих равенств с последующим использованием допущения (П.1.23).

Интегрируя уравнения (3.53) по толщине i -й зоны, учитывая

(П.1.23), получим алгебраические уравнения для определения

При этом используется то же правило формирования источников

147

нейтронов в зоне i , что и в уравнениях (П.1.19), (П.1.21), т.е. на

основе знаков производных dϕi( g ) (Ri ) на границах зон. dr

Уравнения (П.1.19), (П.1.21) или (П.1.25), (П.1.27) обычно решаются численно, используя метод итераций источников. На каждой итерации уравнения вида (П.1.19), (П.1.21) сводятся к конечно-разностным уравнениям, совпадающим по форме с (2.66). Поэтому можно воспользоваться теми же приёмами, которые описаны в разделе 2.5. В связи с этим полезно отметить, что для реактора с небольшим числом слоёв возможно применение метода матричной факторизации. Действительно, ранее указывалось на его низкую эффективность из-за высокой размерности матриц в уравнениях вида (2.73), определяемой числом точек сетки разбиения вдоль осей r или z . Теперь размерности матриц совпадают с числом слоёв n или m вдоль тех же направлений.

Что касается системы алгебраических уравнений (П.1.27), то на каждой итерации при известных источниках

они решаются последовательно, начиная с первой энергетической группы. При этом для любой группы k уравнения для потоков Fi (k ) принимают вид «трехточечных» уравнений, которые проще всего решать методом прогонки.

Приложение 2 Интегро-дифференциальное уравнение

для ценности нейтронов

В многогрупповом диффузионном приближении рассматривается проинтегрированный по всему телесному углу поток нейтронов и принимается, что вероятности взаимодействия нейтронов с ядрами среды не зависят от энергии E в пределах

каждого энергетического интервала Ek . Поэтому и ценности

φ+(k ) (r ) являлись функциями лишь пространственной переменной r и были постоянными для всех нейтронов k-й группы.

148

штрихами) и после рассеяния. В силу этого асимптотический поток нейтронов φ(r , E,Ω) в условно-критическом реакторе становится

функцией переменных (r , E,Ω) и находится из решения интегродифференциального уравнения переноса нейтронов (для сокращения записи через υ обозначены переменные E,Ω , а через

Здесь принимается, что распределение нейтронов деления изотропно по углу и одинаково для всех делящихся ядер, Ω (или

Ω′ ) – множество всех векторов единичной длины Ω (или Ω′), идущих из центра сферы к точкам её поверхности, n – единичный

вектор внешней нормали в точках rs выпуклой границы реактора с вакуумом, Σt (r, E) – полное макроскопическое сечение, а Ws (r,υ′ →υ) – плотность вероятности рассеяния, определяемая равенством

Σs (r , E) Ws (r ,υ′ →υ) = ∑σs,l (E′)Ws,l (υ′ →υ) ρl (r ) ,

l

149

в котором σ s,l (E′) – микроскопическое сечение рассеяния, а ρl (r ) – концентрация ядер сорта l.

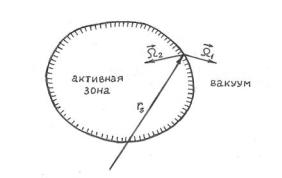
Рис.П.2.1. Выпуклая граница с вакуумом

Теперь изменение асимптотической мощности реактора будет зависеть не только от энергии E и координат точки r , но и от

направления полёта Ω нейтрона в этой точке. В этом проще всего убедиться, рассматривая два способа помещения нейтрона энергии

E в какую-либо точку rs выпуклой границы с вакуумом (рис. П.2.1). Они различаются направлениями полёта Ω1 и Ω2 .Если в

первом случае (вдоль вектора Ω1 ) нейтрон попадает в вакуум и не может изменить мощность реактора, то во втором случае (вдоль вектора Ω2 ) нейтрон имеет конечную вероятность столкнуться с

ядром делящегося материала и вызвать его деление, что приведёт к изменению мощности. Поэтому в общем случае асимптотическая

ценность нейтронов φ+ будет функцией переменных ( r, E,Ω).

Получим уравнение для функции φ + (r , E, Ω) в условно-

критическом реакторе, опираясь на закон сохранения ценностей. С этой целью в единичный объём в окрестности точки

150