КузминАМ Основы теории критичности 2008

Поскольку φ(r ) = Cψ0 (r ) , а ψ0 (r ) – собственная функция задачи (1.6), соответствующая числу α02 , то для вероятности (2.4) будем иметь:

Использование в расчётах формул (2.2) и (2.3) предполагает получение геометрического параметра. Для этого необходимо найти решение задачи (1.6), отвечающее наименьшему

собственному числу α02 . Рассмотрим, как это делается, на примере

реакторов, имеющих активную зону в форме шара или цилиндра конечных размеров. Поскольку эти геометрические формы обладают известными свойствами симметрии, то и собственные функции задачи (1.6) будут удовлетворять таким же свойствам.

Сферический реактор радиуса R, симметричный относительно центра шара r =0 . Собственные функции ψm (r) будут зависеть

лишь от расстояния r от центра шара и их следует искать из решения задачи:

21

Чтобы с помощью этих функций можно было получить ограниченный при всех 0 ≤ r ≤ Rэ поток нейтронов, необходимо

(отрицательные значения m не рассматриваются, поскольку не получаем новых линейно-независимых функций). Отсюда следует, что наименьшее собственное число задачи (2.4)

а асимптотическое распределение нейтронов φ(r) = C sin(α0r) . r

Отметим, что критический радиус сферического реактора, полученный с помощью равенств (2.2) и (2.6), равен:

цилиндра r = 0 и плоскости z = 0 , проходящей перпендикулярно оси через половину высоты. Поэтому собственные функции ψm (r ) зависят лишь от переменных (r,z) и удовлетворяют уравнениям

22

Решение уравнений (2.8) будем искать методом разделения

Подставив (2.9) в уравнение (2.8), получим равенство:

Поскольку частными решениями его являются функции Бесселя действительного аргумента: J 0 ( y), Y0 ( y) , то для общего решения уравнения (2.10) имеем

ϕm (r) = Am(1) J 0 (αr,m r) + Am( 2) Y0 (αr,m r) .

Следует учесть, что функция Y0 (αr,m r) имеет логарифмическую особенность в точке r = 0 . Чтобы при этом поток нейтронов был всюду ограничен, необходимо принять Am( 2) = 0 . Общим решением

уравнения (2.11) является сумма:

ξm (z) = Bm(1) cos(αz,m z) + Bm( 2) sin(αz,m z) ,

23

в которой из соображения симметрии решения относительно

J 0 ( y) . Здесь отрицательные значения m не рассматриваются по

той же причине, что и раньше для сферического реактора. Соотношения (2.12) и (2.13) позволяют сделать вывод о том, что

вцилиндрическом реакторе конечных размеров:

-наименьшее собственное число задачи (2.8) α02 равно

Замечание. При неограниченном возрастании одного из размеров цилиндрический реактор трансформируется либо в плоский реактор толщиной Н, либо в цилиндрический реактор радиуса R бесконечной высоты. Осуществляя в соотношениях (2.14) и (2.15) соответствующие предельные переходы, получим:

- для плоского реактора толщиной Н:

-для бесконечного по высоте цилиндрического реактора радиуса R:

24

2.2. Задача о критичности многозонного реактора

Ограничиваясь аналитическим методом решения задачи, рассмотрим многозонный реактор конечных размеров в одной из простых геометрий. В таком реакторе асимптотический поток

φ(r) = Cψ0 (r) зависит от одной переменной r, а в уравнении

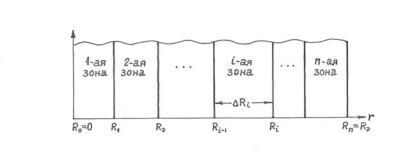
1 – для цилиндрической геометрии и 2 – для сферической геометрии. Будем считать, что реактор симметричен относительно r = 0 и содержит n зон (n ≥ 2) .

Рис.2.1. Модель одномерного многозонного реактора

Пронумеруем зоны в направлении возрастания r (рис.2.1) и

25

Учитывая, что параметры βi2 постоянны в пределах соответствующих зон, приведём уравнение (1.17) для функции

производными до 2-го порядка включительно при r Ri . Чтобы

Отметим, что первое равенство в (2.22) равносильно условию ограниченности решения при r = 0 . Если в плоском реакторе конечных размеров отсутствует плоскость симметрии, то можно по свойствам первой зоны рассчитать длину линейной экстраполяции и, расположив начало координат на экстраполированной границе,

принять ψ0,1 (0) = 0 . Если переменная r в последней зоне может

принимать сколь угодно большие значения (например, рассматривается модель бесконечного сферического реактора), то

26

второе условие в (2.22) заменяет требование ограниченности функции ψ0,n (r) на бесконечности. Однако всегда в той или иной

форме присутствует два граничных условия.

Перейдём теперь к рассмотрению схемы получения критических параметров реактора и асимптотического потока нейтронов. Для этого вначале запишем общее решение каждого из уравнений (2.21) в виде

где Ai , Bi – одновременно не равные нулю коэффициенты, fi (βi r), gi (βi r) – линейно-независимые частные решения,

приведённые в табл. 1 (для разных геометрий в зависимости от значения (2.20) материального параметраω ). Здесь и в дальнейшем

принимается, что βi = + βi2 .

ln r (приν =1) , r−1 (приν = 2) . Если рассматривается неограниченно протяжённая зона без размножения (бесконечный отражатель), то

равенств (2.22), (2.23). При этом полезно сначала сократить число

27

неизвестных, используя граничные условия (2.22). Если это сделано, то для определения оставшихся m = 2n − 2 неизвестных имеем столько же равенств (2.23), называемых часто «условиями сшивки». В результате получим однородную систему линейных уравнений, которая может быть записана в форме:

(2.25)

где X – вектор неизвестных коэффициентов, а M (u) – квадратная матрица порядка m×m с элементами, зависящими от критических параметров u реактора (значения Кэф , размеров и др.).

Нетривиальные решения системы уравнений (2.25) существуют,

представляет собой условие критичности многозонного реактора. Оно устанавливает вполне определённое соотношение между

значениями собственных чисел (включая Кэф ), размерами и составами зон. Рассматривая его как уравнение относительно u , можно найти критическое значение u = u0 (например, значение Кэф , если размеры и свойства зон известны, или обогащение

топлива в активной зоне критического реактора и т.п.). При этом важно иметь в виду, что уравнение (2.26) имеет бесконечное

множество решений, и следует выбрать такое u0 , которое в дальнейшем приведёт к построению собственной функции ψ0 (r) ,

соответствующей ведущему собственному числу задачи (1.17). Например, если задача о критичности реактора рассматривается в

постановке 2, то в качестве Кэф нужно взять самое большое

значение, при котором выполняется равенство (2.26).

После нахождения критических параметров приступают к

искать отличный от нуля определитель матрицы ˆ , имеющий

M

28

наивысший порядок. Пусть таким окажется определитель порядка

A2 , B2 , A3 , B3 ,…, An . После этого нетрудно, используя выражения

уравнений (2.25) будет существовать, когда хотя бы два неизвестных будут независимыми. Например, если такими

сделанных в главе 1 выводу: ведущему собственному числу Кэф

соответствует единственная собственная функция.

Отметим, что изложенный выше способ получения асимптотического потока нейтронов легко распространить на реакторы, которые имеют конечные размеры, но свойства зон не меняются в направлениях, перпендикулярных оси r. Такие реакторы в дальнейшем будем называть конечными одномерными реакторами. Среди них важное место занимают цилиндрические реакторы конечной высоты, в которых поток нейтронов зависит от 2-х переменных: расстояния r от оси симметрии и расстояния z от плоскости симметрии, проходящей через половину высоты H цилиндра. В этом случае асимптотический поток нейтронов

φ0 (r, z) = Cψ0 (r, z) , а задача о критичности решается при условиях типа (2.30) и дополнительных требованиях:

29

где ± Н2э – координаты торцевых экстраполированных границ с

вакуумом.

В этом случае пространственные переменные разделяются и решение ψ0 (r, z) ищется в виде произведения

ψ0 (r, z) = ϕ0 (r)ξ0 (z) , ξ0 (z) = B0 cos(αz z) ,

(i =1,2,…, n)

при условиях типа (2.22), (2.23).

Задача (2.27), (2.22), (2.23) отличается от задачи (2.20) - (2.23)

утечку нейтронов в аксиальном направлении. Очевидно, решение уравнений (2.27) находится так же, как уравнений (2.21). При этом

цилиндрической геометрии в зависимости от знака разности

±βi2 −αz2 .

2.3.Влияние отражателя на критические параметры реактора

Вкачестве примера рассмотрим решение задачи о критичности сферически симметричного реактора, состоящего из активной зоны

30