
Signal Processing of Random Physiological Signals - Charles S. Lessard
.pdf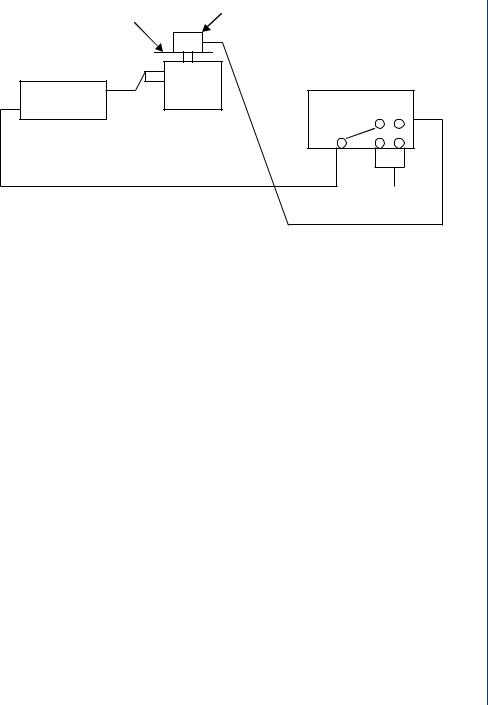
|
COHERENCE FUNCTION FROM SPECTRAL ANALYSIS 211 |
||||||
Test |
|
|
|
|
|
|
Accelerometer |
|
|
|
|
|
|
|
|
specimen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Power |
Shaker |
|
|
3582A |
|
||
amplifier |
|
||
A |
B |
||
|
|||
|
PRN |
|
FIGURE 18.4: Test setup. The possible results in the evaluation would be (a) normal transfer function response or (b) transfer function is contaminated by vibration from loose hardware during testing of specimen
was 0.83/(1 − 0.83), so the coherence function is an alternative method of measuring the signal-to-noise ratio or an input–output system.
Lessard [3] used the coherence function to determine the cause-and-effect relationship between the output of the vestibular system and pseudorandom angular velocity input. The subject was subjected to pseudorandom angular velocity the saccade of the horizontal eye movement was converted to a signal. A full analysis of the output frequencies was performed. The coherence function analysis was performed as the last step in the analysis. This project was done with the objective of determining the nature and causes of space sickness.
18.5PROBLEMS THAT LIMIT THE APPLICATION OF COHERENCE
There are numerous problems that limit the application. The major problems will be listed without discussion. Among these problems are
1.inaccurate source measurements,
2.source measurement interference,

212SIGNAL PROCESSING OF RANDOM PHYSIOLOGICAL SIGNALS
3.correlation among sources,
4.input–output time-delay errors,
5.input measurement noise,
6.input–output nonlinearities,
7.input–output feedback,
8.reverberation effects, and
9.common source periodicities.
18.6CONCLUSION
The coherence function, like many of the other mathematical operations used in signal processing, is susceptible to abuses by researchers who intentionally misapply its use or is not well informed with regard to its limitations. The coherence function should be used to establish a relationship between input and output of a system. None of the literature supports the idea of using the coherence function to compare two output signals such as the electromyograms (EMG) from two different muscles. Finally, as in all types of scientific tools, all assumptions must be met if the results are to be interpreted correctly.
18.7REFERENCES
1.Bendat, J. S. and Piersol, A. G. Random Data: Analysis and Measurement Procedures. Wiley Interscience, 1971.
2.Bendat, J. S. “Statistical Errors in Measurement of the Coherence Function and Input–Output Quantities,” Journal of Sound and Vibration, September 1978.
3.Lessard, C. S. “Analysis of Nystagmus Response to Pseudorandom Velocity Input,”
Compute Methods and Programs in Biomedicine, Vol. 23, 1986.
4.Neter, J., Wasserman, W., and Hunter M.H., Applied Linear Regression Models. Irwin, 1983.

COHERENCE FUNCTION FROM SPECTRAL ANALYSIS 213
5.Roth, P. R. “Measurements Using Digital Signal Analysis,” IEEE Spectrum, April 1971.
6.Roth, P. R. “How to Use the Spectrum and Coherence Function,” Sound and Vibration, January 1971.
7.Winer, B. J. Statistical Principles in Experimental Design. McGraw-Hill, 1971.


216 SIGNAL PROCESSING OF RANDOM PHYSIOLOGICAL SIGNALS
records x(t) and y (t) of unlimited length T, the one-sided cross-spectrum is given by (19.1).
G x y ( f ) = T→∞ T E |
X |
|
f |
|
T |
|
Y |
|
f |
|
T |
|
|
|||
Lim |
2 |
|
|
|
( |
|
, |
|
) |
|
( |
|
, |
|
) |
(19.1) |
|
|
|
|
|
|
|
|
|||||||||
where X( f, T ) is the conjugate of the input and Y ( f, T) are the finite Fourier transforms of x(t) and y (t), respectively.
It should be noted that the raw spectrum (no averages) of a finite length has the same equation as (19.1), without the limit as given by (19.2) and will have a resolution
bandwidth given by (19.3). |
|
|
|
|
|
|
|
|
ˆ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
G x y ( f ) = |
|
T |
[X( f )Y ( f )] |
(19.2) |
||||
Be = |
f = |
1 |
|
(19.3) |
||||
|
|
|||||||
T |
||||||||
The ordinary coherence function is defined by (19.4).
γ 2 |
= |
|G x y |2 |
(19.4) |
|
G x x G y y |
||||
x y |
The corresponding variance errors for “smooth” estimates of all of the “raw” es-
timates in (19.4) will be reduced by a factor of nd when averages are taken over nd statistically independent “raw” quantities. To be specific, the variance expressions are given by (19.5), (19.6), and (19.7).
˜ |
] = |
|
G 2x x |
|
|
|
|
(19.5) |
||||
Var[G x x |
|
nd |
|
|
|
|
||||||
˜ |
|
|
|
G 2y y |
|
|||||||
Var[G y y |
] = |
|
nd |
|
|
|
|
(19.6) |
||||
˜ |
|
|
|
|G 2x y | |
|
|
|
|
||||
Var[|G x y |] = |
γx2y nd |
|
|
|
(19.7) |
|||||||
Then, the normalized root-mean-square errors, which are the same as the nor- |
||||||||||||
malized random errors, are given by (19.8), (19.9), and (19.10), respectively. |
|
|||||||||||
˜ |
|
1 |
|
|
|
|
|
|
|
|
||
ε[G x x ] = |
√ |
|
|
|
|
|
(19.8) |
|||||
nd |
||||||||||||
˜ |
|
1 |
|
|
|
|
|
|
|
|
||
ε[G y y ] = |
√ |
|
|
|
|
|
(19.9) |
|||||
nd |
||||||||||||
˜ |
|
1 |
|
|
|
|
|
|
|
|||
ε[|G x y |] = |
|γx y |√ |
|
|
|
(19.10) |
|||||||
nd |
|
|
||||||||||

|
|
|
|
|
ERROR IN RANDOM DATA ESTIMATE ANALYSIS 217 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
TABLE 19.1: Normalized Random Errors for Spectral Estimates |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ESTIMATE |
NORMALIZED RANDOM ERROR, ε |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
G x x ( f ), |
G y y ( f ) |
√ |
nd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|G x y ( f )| |
|
|γx y ( f )|√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
nd |
|
|
|
|
|
|
|
|
|
|
||||||
|
ˆ |
|
|
[G x x ( f )G y y ( f ) + Cx2y ( f ) − Q2x y ( f )]1/2 |
|
|
|
|
|
|||||||||
|
C x y ( f ) |
|
|
|
|
|
|
|
Cx y ( f )√ |
2nd |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
[G x x ( f )G y y ( f ) + Q2x y |
( f ) − Cx2y ( f )]1/2 |
|
|
|
|
|
||||||||
|
Qx y ( f ) |
|
|
|
|
|
|
|
Qx y ( f )√ |
2nd |
|
|
|
|
|
|
||
The quantity |γx y | is the positive square root of γx2y . Note that ε for the cross-spectrum |
|
|||||||||||||||||
|
|
ˆ |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
||||
magnitude estimate |G x y |varies inversely with γx y |
and approaches √ |
|
|
as γx y ap- |
|
|||||||||||||
nd |
|
|||||||||||||||||
proaches 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A summary is given in Table 19.1 on the main normalized random error formulas |
|
|||||||||||||||||
for various spectral density estimates. The number of averages nd represents nd distinct |
|
|||||||||||||||||
(nonoverlapping) records, which are assumed to contain statistically different information |
|
|||||||||||||||||
from record to record. These records may occur by dividing a long stationary ergodic |
|
|||||||||||||||||
record into nd parts, or they may occur by repeating an experiment nd times under |
|
|||||||||||||||||
similar conditions. With the exception of autospectrum error estimation equation (19.8) |
|
|||||||||||||||||
and (19.9), all other error formulas are functions of frequency. Unknown true values |
|
|||||||||||||||||
of desired quantities are replaced by measured values when one applies these results to |
|
|||||||||||||||||
evaluate the random errors in actual measured data. |
|
|
|
|
|
|
|
|
||||||||||
Let us work through an example to illustrate calculating the random errors in Fre- |
|
|||||||||||||||||
quency Response Transfer Function Estimate. Suppose the frequency response function |
|
|||||||||||||||||
between two random signals x(t) and y (t) is estimated using nd = 50 averages. Assume |
|
|||||||||||||||||
that the coherence function at one frequency of interest is γx2y ( f1) = 0.10 and at a second |
|
|||||||||||||||||
frequency of interest is γx2y ( f2) = 0.90, the problem is to determine the random errors |
|
|||||||||||||||||
in the frequency response function gain and phase estimates at the two frequencies of |
|
|||||||||||||||||
|
||||||||||||||||||
interest. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

218 SIGNAL PROCESSING OF RANDOM PHYSIOLOGICAL SIGNALS
TABLE 19.2: Multiple-Input/Output Model Estimates
FUNCTION BEING |
NORMALIZED RANDOM |
|||||||||||||||||
ESTIMATED |
|
|
ERROR, ε |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γˆ 2 |
( f ) |
|
2[1 − γx2y ( f )] |
|
|
|
|
|
||||||||||
|
|
|γx y ( f )|√ |
|
|
|
|
|
|||||||||||
x y |
|
|
|
nd |
|
|
|
|
|
|
|
|
|
|||||
ˆ |
2 |
ˆ |
[2 − γx2y ( f )]1/2 |
|||||||||||||||
G vv( f ) = γˆx y |
( f )G y y ( f ) |
|
|γx y ( f )|√ |
|
|
|
|
|
|
|
|
|
|
|||||
|
nd |
|
|
|
|
|
|
|
|
|
||||||||
ˆ |
|
|
[1 − γx2y ( f )]1/2 |
|||||||||||||||
|Hx y ( f )| |
|
|
|γx y ( f )|√ |
|
|
|
|
|
|
|
||||||||
|
|
2nd |
|
|
|
|
|
|
||||||||||
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
[1 − γx2y ( f )]1/2 |
|||||||
φx y ( f ) |
|
S.D. [φx y ( f )] |
≈ |
|γx y ( f )|√ |
|
|
|
|||||||||||
|
2nd |
|
||||||||||||||||
Equations (19.11) and (19.12) are used to calculate the variance and the normalized random error of the transfer function, respectively.
˜ |
1 − γx2y |
Hx y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Var[ Hx y ] ≈ |
|
|
|
|
|
|
|
(19.11) |
|
2γx2y nd |
|
|
|
|
|
||||
˜ |
˜ |
|
|
|
|
2 1/2 |
|
||
SD [ Hx y ] |
1 − γx y |
|
|||||||
ε[ Hx y ] = |
Hx y |
|
≈ |
|
|
√ |
|
|
(19.12) |
|
|
γx y |
2nd |
||||||
Then from (19.12), the normalized random error in the gain factor estimates at frequencies f1and f2 will be given by (19.13) and (19.14).
ε |
˜ |
|
(1 − 0.10)1/2 |
|
. |
|
|
|||||
|
[ Hx y ( f1) ] |
= |
|
(0.32)(10) |
= 0 |
|
30 |
(19.13) |
||||
ε |
˜ |
|
(1 − 0.90)1/2 |
|
. |
|
|
|||||
|
[ Hx y ( f2) ] |
= |
|
(0.95)(10) |
= 0 |
|
033 |
(19.14) |
||||
The phase angle estimate, from the standard deviation (S D), is given by (19.15). |
||||||||||||
|
|
|
|
|
1/2 |
|
|
|
|
|
||
|
˜ |
1 − γx2y |
|
˜ |
|
|
||||||
|
SD [φx y ] ≈ |
|
√ |
|
|
≈ |
ε Hx y |
(19.15) |
||||
|
γx y |
2nd |
||||||||||

ERROR IN RANDOM DATA ESTIMATE ANALYSIS 219
Applying (19.15), the results also constitute approximations for the standard deviation (not normalized) in the phase factor estimate calculation as follows.
˜ |
˜ |
SD [φx y ( f1)] = 0.30 radians |
SD [φx y ( f2)] = 0.033 radians |
= 17 degrees |
= 1.9 degrees |
Hence, the estimates made with a coherence of γx2y ( f2) = 0.90 are almost ten times as accurate as those made with a coherence of γx2y ( f1) = 0.10.
19.2 SUMMARY
A summary is given in Table 19.2 on the main normalized random error formulas for single-input/output model estimates.
