II. Модели одномерных временных рядов (динамические ряды)

Если совокупность значений какого – либо показателя меняется за несколько последовательных моментов времени, то для его изучения применяют модель временного ряда.

Временной ряд имеет как правило тренд (Т), сезонную компоненту (S), случайную составляющую (Е).

Если амплитуда колебаний сезонной компоненты постоянна, то применяют аддитивную модельвременного ряда (У_t = Т + S + Е).

Если амплитуда колебаний сезонной компоненты меняется с течением времени, то выбирают мультипликативную модель временного ряда

(У_t = Т * S * Е).

Обратить внимание! При выполнении дипломной работы студентами специальности «Бухгалтерский учет, анализ и аудит» модели одномерных временных рядов могут быть использованы:

• для прогнозирования анализируемых финансовых показателей деятельности объектов исследования, осуществляющих коммерческую деятельность, на предстоящий период. Обоснование прогнозных значений показателей в зависимости от темы дипломной работы может быть использовано автором дипломной работы для формирования выводов при принятии конкретных управленческих решений, позволяющих сохранять или принять оперативные меры по предотвращению негативных тенденций. Кроме того, прогнозные значения могут быть использованы при формировании стратегии экономического развития исследуемого субъекта на перспективу;

• для обоснования прогнозных значений показателей смет (бюджетов) субъектов, осуществляющих деятельность за счет финансирования средств бюджетов различных уровней (государственных, казенных, муниципальных, унитарных и т. д.). Авторы дипломных работ, объектом исследования которых являются подобные субъекты, могут аргументировать значения показателей в зависимости от темы исследования(фонд заработной платы, материальные расходы и т. д.). В соответствии с действующей редакцией бюджетного законодательства вопросы прогнозирования в настоящее время достаточно актуальны.

• при формировании выводов о достоверности определенных прогнозных значений дипломники могут использовать указанные в методических рекомендациях значение коэффициентов корреляции, детерминации и средней ошибки аппроксимации.

Замечание 1. Эти модели могут также быть использованы при оптимизации остатка денежных средств, нормировании запасов, описании расходов.

Замечание 2. В последующих пунктах мы опишем методику расчета аддитивной и мультипликативной модели временного ряда, имеющей линейный тренд. Если тренд не является линейным, то такую методику расчета компонент временного ряда применять нельзя, поэтому в Приложении 1 приведено описание расчетов этой модели временного ряда с помощью электронной таблицы, созданной в программе Microsoft Excel 2007.

В Приложении 2 описана регрессионная модель, полученная с помощью электронной таблицы, созданной в программе Microsoft Excel 2007.

2.1 Аддитивная модель временного ряда (У_t = Т + S + Е)

Рассмотрим построение модели аддитивного ряда на примере изучения объемов потребления электроэнергии (млн кВТ*ч) жителями региона за 16 кварталов и на основании полученной модели спрогнозируем объем потребляемой электроэнергии на следующие полгода. Построенный пример описан в .

Пусть известный объем потребляемой электроэнергии задан таблицей 1.

Таблица 1- Потребление электроэнергии жителями региона, млн кВТ*ч

№ кварт.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Объем электроэнергии (млн кВТ*ч)	6,0	4,4	5,0	9,0	7,2	4,8	6,0	10	8,0	5,6	6,4	11	9,0	6,6	7,0	10.8

Построим график временного ряда, откладывая по оси Ох время (квартал), а по оси Оу объем потребляемой электроэнергии (млн кВТ*ч).

Заметим, что данный ряд имеет тренд (возрастающую тенденцию), сезонные колебания (с периодом 4) и случайную составляющую.

Учитывая, что амплитуда сезонных колебаний практически постоянна делаем вывод об аддитивности данного временного ряда (У_t = Т + S + Е).

Рассчитаем значения Т, S и Е по следующему алгоритму:

1. Выравниваем исходный ряд методом скользящей средней

Для этого произведем расчет сезонной компоненты. Результаты оформим в расчетную таблицу 2.

Таблица 2- Расчет оценок сезонной компоненты в аддитивной модели

Номер квартала	Потребление электроэнергии	Итого за четыре квартала	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	6,0	–	–	–	–
2	4,4	24,4	6,10	–	–
3	5,0	25,6	6,40	6,250	–1,250
4	9,0	26,0	6,50	6,450	2,550
5	7,2	27,0	6,75	6,625	0,575
6	4,8	28,0	7,00	6,875	–2,075
7	6,0	28,8	7,20	7,100	–1,100
8	10,0	29,6	7,40	7,300	2,700
9	8,0	30,0	7,50	7,450	0,550
10	5,6	31,0	7,75	7,625	–2,025
11	6,4	32,0	8,00	7,875	–1,475
12	11,0	33,0	8,25	8,125	2,875
13	9,0	33,6	8,40	8,325	0,675
14	6,6	33,4	8,35	8,375	–1,775
15	7,0	–	–	–	–
16	10,8	–	–	–	–

Таблица расчета оценок сезонной компоненты в аддитивной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известный объем потребляемой электроэнергии (млн кВТ*ч);

3 столбец – складываем последовательно значения четырех ячеек 2 столбца и записываем их на одну клетку ниже;

4 столбец – каждое значение 3 столбца делим на 4 (период сезонных колебаний);

5 столбец – складываем последовательно значения двух ячеек 4 столбца, делим эту сумму на 2 и записываем на одну клетку ниже;

6 столбец – из элементов 2 столбца вычитаем элементы 5 столбца.

2. Рассчитаем значения сезонной компоненты S

Для этой цели составим следующую расчетную таблицу 3, в которую последовательно разместим данные из 6 столбца табл. 2.

Таблица 3- Расчет значений сезонной компоненты в аддитивной модели

Показатель	Год	Номер квартала
		I	II	III	IV
	1	–	–	–1,250	2,550
	2	0,575	–2,075	–1,100	2,700
	3	0,550	–2,025	–1,475	2,875
	4	0,675	–1,775	–	–
Итого за квартал		1,800	–5,875	–3,825	8,125
Средняя оценка сезонной компоненты (		0,600	–1,958	–1,275	2,708
Скорректированная сезонная компонента		0,581	–1,977	–1,294	2,690

Средняя оценка сезонной компоненты () рассчитывается как итого за квартал /3.

В аддитивных моделях с сезонной компонентой предполагается , что сезонные воздействия за период взаимопогашаются. Это означает, что сумма значений сезонной компоненты по всем кварталам должна быть равна 0.

Для данной модели имеем 0,600+ (–1,958) + (–1,275) + 2,708 = 0,075 0.

Определим корректирующий коэффициент k = 0,075/4 = 0,01875.

Рассчитаем скорректированные значения сезонной компоненты, как разность между ее средней оценкой и корректирующим коэффициентом k:

k.

Проверим условие равенства нулю суммы значений сезонной компоненты: 0,581 – 1,977 – 1,294 + 2,690 = 0.

3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда ( Y – S = T + E). Расчеты оформим в виде таблицы 4.

Таблица 4. Расчет выровненных значений Т и ошибок Е в аддитивной модели

t	yt	Si	yt – Si	T	T+S	E	E2
1	2	3	4	5	6	7	8
1	6,0	0,581	5,419	5,893	6,474	-0,474	0,224
2	4,4	–1,977	6,337	6,08	4,103	0,297	0,088
3	5,0	–1,294	6,294	6,267	4,973	0,027	0,001
4	9,0	2,690	6,310	6,454	9,144	-0,144	0,021
5	7,2	0,581	6,619	6,641	7,222	-0,022	0,001
6	4,8	–1,977	6,777	6,828	4,851	-0,051	0,003
7	6,0	–1,294	7,294	7,015	5,721	0,279	0,078
8	10,0	2,690	7,310	7,202	9,892	0,108	0,012
9	8,0	0,581	7,419	7,389	7,97	0,03	0,001
10	5,6	–1,977	7,577	7,576	5,599	0,001	0.000
11	6,4	–1,294	7,694	7,763	6,469	-0,069	0,005
12	11,0	2,690	8,310	7,95	10,64	0,36	0,130
13	9,0	0,581	8,419	8,137	8,718	0,282	0,080
14	6,6	–1,977	8,577	8,324	6,347	0,253	0,064
15	7,0	–1,294	8,294	8,511	7,217	-0,217	0,047
16	10,8	2,690	8,110	8,698	11,388	-0,588	0,346

Таблица расчета выровненных значений Т и ошибок Е в аддитивной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известный объем потребляемой электроэнергии (млн кВТ*ч);

3 столбец – выписываем последовательно значения из последней строки таблицы 3;

4 столбец – из значений 2 столбца вычитаем значения 3 столбца;

5 столбец – для того, чтобы заполнить этот столбец, рассчитаем тренд (Т) с помощью следующего шага 4; только затем перейдем к заполнению оставшихся столбцов таблицы 4.

4. Определим компоненту тренда (Т) данной модели.

Анализ графика временного ряда свидетельствует о линейном характере тренда. Воспользуемся для расчета параметров тренда методом наименьших квадратов. Для этого составим расчетную таблицу 5, считая независимой переменной время (номер квартала), а зависимой переменной T+E = y_t – S_i (объем потребляемой электроэнергии).

Таблица 5- Расчет параметров тренда (Т)

№	x	y	x2	y2	xy		y-	Аi
	1	2	3	4	5	6	7	8
1	1	5,419	1	29,36556	5,419	5,893	-0,474	8,74700
2	2	6,337	4	40,15757	12,674	6,08	0,257	4,05555
3	3	6,294	9	39,61444	18,882	6,267	0,027	0,42898
4	4	6,31	16	39,8161	25,24	6,454	-0,144	2,28209
5	5	6,619	25	43,81116	33,095	6,641	-0,022	0,33238
6	6	6,777	36	45,92773	40,662	6,828	-0,051	0,75255
7	7	7,294	49	53,20244	51,058	7,015	0,279	3,82506
8	8	7,31	64	53,4361	58,48	7,202	0,108	1,47743
9	9	7,419	81	55,04156	66,771	7,389	0,03	0,40437
10	10	7,577	100	57,41093	75,77	7,576	0,001	0,01320
11	11	7,694	121	59,19764	84,634	7,763	-0,069	0,89680
12	12	8,31	144	69,0561	99,72	7,95	0,36	4,33213
13	13	8,419	169	70,87956	109,447	8,137	0,282	3,34957
14	14	8,577	196	73,56493	120,078	8,324	0,253	2,94975
15	15	8,294	225	68,79044	124,41	8,511	-0,217	2,61635
16	16	8,11	256	65,7721	129,76	8,698	-0,588	7,25031
Сумма	136	116,76	1496	865,0443	1056,1	116,728		43,7135
Ср.зн.	8,5	7,2975	93,5	54,06527	66,0062	7,2955		2,732094

Таблица расчета параметров линейного тренда Т в аддитивной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известный объем потребляемой электроэнергии (млн кВТ*ч) выбирается из 4 столбца таблицы 4;

3 столбец – возводим в квадрат значения 1 столбца;

4 столбец – возводим в квадрат значения 2 столбца;

5 столбец – умножаем значения 3 столбца на 4 столбец;

Для расчета 6 столбца таблицы 5 находим параметры тренда у = а+ вх.

Для этого составляем систему нормальных уравнений в виде:

,

.

Решим эту систему по правилу Крамера, составим определители:

,

,

.

Тогда а = =/= 5,7065,

b = =

Составляем уравнение тренда у = 5,7065 + .

Определим насколько хорошо согласованы расчетные и фактические данные. Для этого произведем расчет коэффициента корреляции, детерминации и вычислим среднюю ошибку аппроксимации.

Коэффициент корреляции вычислим по формуле

.

Коэффициент детерминации равен ² = 92,5%.

Средняя ошибка аппроксимации получится после того, как будет заполнен 6 столбец таблицы 5. Для того чтобы заполнить 6 столбец в уравнение тренда у = 5,7065 + вместо t подставим значения из 1 столбца. В 7 столбик занесем разность между 2 и 6 столбцами. И, наконец, в 8 столбик занесем отношение 7 столбика ко 2, взятое по модулю, и это число умножим на 100%. Учитывая среднее значение, получим, что . Заметим, что все три показателя находятся в пределах нормы, значит, модель тренда соответствует реальности.

Теперь мы можем продолжить заполнение таблицы 4.

5 столбец совпадает с 6 столбцом таблицы 5.

6 столбец получаем, складывая значения 3 столбца и 5 столбца таблицы 4.

7 столбец получаем как разность между вторым столбцом и 6, он показывает случайную величину, то есть абсолютную ошибку.

8 столбец рассчитываем, возводя в квадрат значения 7 столбца. Он позволяет оценить качество полученной модели. Складывая все значения этого столбца, получаем 1,0994.

Тогда сумма квадратов отклонений уровней ряда от его среднего значения равна: (1 - 1,0994/ 90,16)*100=98,78%.

Следовательно, можно сказать, что аддитивная модель объясняет 98,78% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.

Сравнение модели с исходным графиком, можно посмотреть на рисунке 2.

Рисунок 2

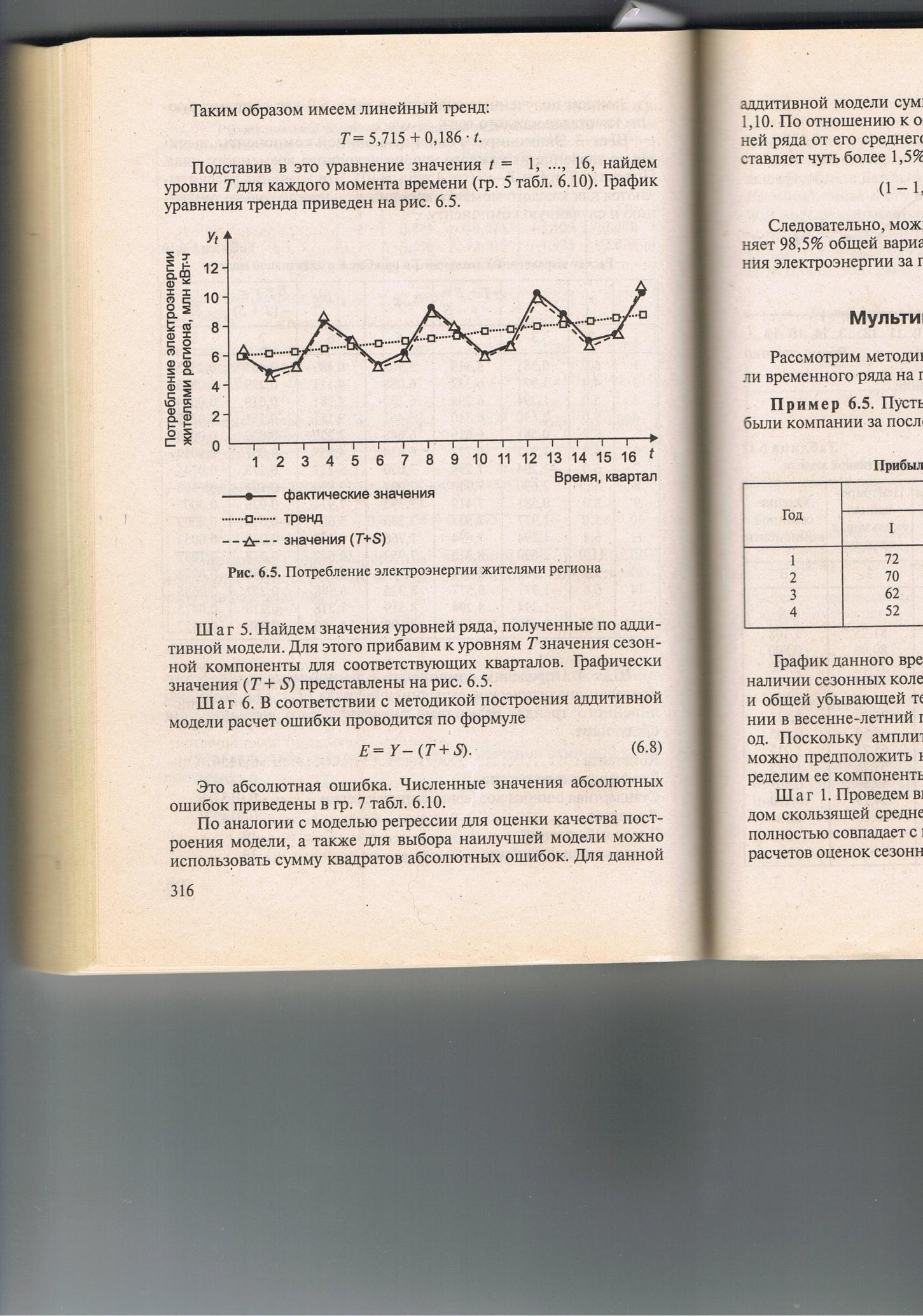
Спрогнозируем потребление электроэнергии жителями региона в течение первого полугодия ближайшего года.

У = У₁₇ + У₁₈, где У₁₇ = Т₁₇ + S₁₇, а У₁₈ = Т₁₈ + S₁₈.

Заметим, что S₁₇ = 0,581, а S₁₈ = –1,977 (взяты из таблицы 3).

Т₁₇ =5,7065 + , а Т₁₈ =5,7065 + =9,0761

Тогда У = 0,581+ 9,0761–1,977 = 16,569. Значит, прогноз составляет 16,569 млн кВтч.

Вывод: прогноз потребления электроэнергии на ближайшие полгода составит 16,569 млн кВтч.

2.2 Мультипликативная модель временного ряда (У_t = Т S Е)

Рассмотрим построение модели мультипликативного ряда на примере изучения прибыли компании за последние 4 года и на основании полученной модели спрогнозируем прибыль компании на следующие полгода. Построенный пример описан в .

Пусть имеются поквартальные данные прибыли компании за последние 4 года (тыс. долл США) таблица 1.

Таблица 1- Поквартальные данные прибыли компании

Год	Квартал
	I	II	III	IV
1	72	100	90	64
2	70	92	80	58
3	62	80	68	48
4	52	60	50	30

Построим график временного ряда, откладывая по оси Ох время (квартал), а по оси Оу прибыль компании в (тыс. долл. США).

Заметим, что данный ряд имеет тренд (убывающую тенденцию), сезонные колебания (с периодом 4) и случайную составляющую. Учитывая, что амплитуда сезонных колебаний уменьшается с течением времени предполагаем мультипликативность данного временного ряда (У_t = Т S Е).

Рассчитаем значения Т, S и Е по следующему алгоритму:

1. Выравниваем исходный ряд методом скользящей средней

Для этого произведем расчет сезонной компоненты.

Результаты оформим в расчетную таблицу 2.

Таблица 2 . Расчет оценок сезонной компоненты в мультипликативной модели

Номер квартала	Потребление электроэнергии	Итого за четыре квартала	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	72	–	–	–	–
2	100	326	81,5	–	–
3	90	324	81,0	81,25	1,108
4	64	316	79,0	80,00	0,8
5	70	306	76,5	77,75	0,9
6	92	300	75,0	75,75	1,215
7	80	292	73,0	74,00	1,081
8	58	280	70,0	71,5	0,811
9	62	268	67,0	68,5	0,905
10	80	258	64,5	65,75	1,217
11	68	248	62,0	63,25	1,075
12	48	228	57,0	59,50	0,807
13	52	210	52,5	54,75	0,905
14	60	192	48,0	50,25	1,194
15	50	–	–	–	–
16	30	–	–	–	–

Таблица расчета оценок сезонной компоненты в мультипликативной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известная прибыль компании (тыс. долл. США);

3 столбец – складываем последовательно значения четырех ячеек 2 столбца и записываем их на одну клетку ниже;

4 столбец – каждое значение 3 столбца делим на 4 (период сезонных колебаний);

5 столбец – складываем последовательно значения двух ячеек 4 столбца, делим эту сумму на 2 и записываем на одну клетку ниже;

6 столбец – элементы 2 столбца разделим на элементы 5 столбца.

2. Рассчитаем значения сезонной компоненты S.

Для этой цели составим следующую расчетную таблицу 3, в которую последовательно разместим данные из 6 столбца табл. 2.

Таблица 3. Расчет значений сезонной компоненты в мультипликативной модели

Показатель	Год	Номер квартала
		I	II	III	IV
	1	–	–	1,108	0,800
	2	0,900	1,215	1,081	0,817
	3	0,905	1,217	1,075	0,807
	4	0,955	1,194	–	–
Итого за квартал		2,755	3,626	3,264	2,424
Средняя оценка сезонной компоненты (		0,918	1,209	1,088	0,808
Скорректированная сезонная компонента		0,913	1,202	1,082	0,803

Средняя оценка сезонной компоненты () рассчитывается как итого за квартал /3.

В мультипликативных моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. Это означает, что сумма значений сезонной компоненты по всем кварталам должна быть равна периоду (в нашем случае 4).

Для данной модели имеем 0,918+ 1,209 + 1,088 + 0,808 = 4,023 4.

Определим корректирующий коэффициент k = 4/4,023 = 0,9943.

Рассчитаем скорректированные значения сезонной компоненты, как произведение ее средней оценки на корректирующий коэффициент k:

k.

Проверим условие равенства четырем суммы значений сезонной компоненты: 0,913+1,202 +1,082 +0,803 = 4.

3. Элиминируем влияние сезонной компоненты, разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты (Y/ S = T 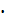E). Расчеты оформим в виде таблицы 4.

Таблица4. Расчет выровненных значений Т и ошибок Е в аддитивной модели

t	yt	Si	yt / Si	T	TS	E	Е/	E2
1	2	3	4	5	6	7	8	9
1	72	0,913	78,86	87,81	80,17	0,898	-8,17	5,419
2	100	1,202	83,19	85,04	102,21	0,978	-2,21	6,337
3	90	1,082	83,18	82,27	89,01	1,011	0,98	6,294
4	64	0,803	79,70	79,5	63,83	1,002	0,16	6,31
5	70	0,913	76,67	76,73	70,05	0,999	-0,05	6,619
6	92	1,202	76,54	73,96	88,9	1,035	3,10	6,777
7	80	1,082	73,94	71,19	77,03	1,039	2,97	7,294
8	58	0,803	72,23	68,42	54,94	1,056	3,05	7,31
9	62	0,913	67,91	65,65	59,94	1,034	2,06	7,419
10	80	1,202	66,56	62,88	75,58	1,058	4,42	7,577
11	68	1,082	62,85	60,11	65,04	1,046	2,96	7,694
12	48	0,803	59,78	57,34	46,04	1,042	1,96	8,31
13	52	0,913	56,96	54,57	49,82	1,044	2,18	8,419
14	60	1,202	49,92	51,8	62,26	0,96	-2,26	8,577
15	50	1,082	46,21	49,03	53,05	0,94	-3,05	8,294
16	30	0,803	37,36	46,26	37,15	0,81	-7,15	8,11

Таблица расчета выровненных значений Т и ошибок Е в мультипликативной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известная прибыль компании;

3 столбец – выписываем последовательно значения из последней строки таблицы 3;

4 столбец – значения 2 столбца разделим на значения 3 столбца;

5 столбец – для того, чтобы заполнить этот столбец, рассчитаем тренд (Т) с помощью следующего шага 4; только затем перейдем к заполнению оставшихся столбцов таблицы 4.

4. Определим компоненту тренда (Т) данной модели.

Анализ графика временного ряда свидетельствует о линейном характере тренда.

Воспользуемся для расчета параметров тренда методом наименьших квадратов. Для этого составим расчетную таблицу, считая независимой переменной время (номер квартала), а зависимой переменной TE = y_t / S_i (прибыль компании). Для этих целей составим расчетную таблицу 5.

Таблица 5- Расчет параметров тренда (Т)

№	x	y	x2	y2	xy		y-	Аi
1	2	3	4	5	6	7	8	9
1	1	78,86	1	6218,9	78,86	87,81	-8,95	11,34923
2	2	83,19	4	6920,576	166,38	85,04	-1,85	2,223825
3	3	83,18	9	6918,912	249,54	82,27	0,91	1,094013
4	4	79,7	16	6352,09	318,8	79,5	0,2	0,250941
5	5	76,67	25	5878,289	383,35	76,73	-0,06	0,078257
6	6	76,54	36	5858,372	459,24	73,96	2,58	3,370787
7	7	73,94	49	5467,124	517,58	71,19	2,75	3,719232
8	8	72,23	64	5217,173	577,84	68,42	3,81	5,274817
9	9	67,91	81	4611,768	611,19	65,65	2,26	3,327934
10	10	66,56	100	4430,234	665,6	62,88	3,68	5,528846
11	11	62,85	121	3950,123	691,35	60,11	2,74	4,359586
12	12	59,78	144	3573,648	717,36	57,34	2,44	4,081633
13	13	56,96	169	3244,442	740,48	54,57	2,39	4,195927
14	14	49,92	196	2492,006	698,88	51,8	-1,88	3,766026
15	15	46,21	225	2135,364	693,15	49,03	-2,82	6,102575
16	16	37,36	256	1395,77	597,76	46,26	-8,9	23,82227
Сумма	136	1071,86	1496	74664,79	8167,36	1072,56		82,54589
Ср.знач.	8,5	66,99	93,5	4666,549	510,46	67,035		5,159118

Таблица расчета параметров линейного тренда Т в мультипликативной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известная прибыль компании выбирается из 4 столбца таблицы 4;

3 столбец – возводим в квадрат значения 1 столбца;

4 столбец – возводим в квадрат значения 2 столбца;

5 столбец – умножаем значения 3 столбца на 4 столбец;

Для расчета 6 столбца таблицы 5 находим параметры тренда у = а+ вх.

Составляем систему нормальных уравнений в виде:

,

.

Решая эту систему по правилу Крамера, составим определители:

,

,

.

Тогда а = =/= 90,57575,

b = =

Уравнение тренда у = 90,58.

Определим насколько хорошо согласованы расчетные и фактические данные. Для этого произведем расчет коэффициента корреляции, детерминации и вычислим среднюю ошибку аппроксимации.

Коэффициент корреляции вычислим по формуле

.

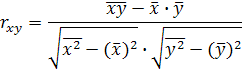
Коэффициент детерминации равен ² = 92,3%.

Средняя ошибка аппроксимации получится после того, как будет заполнен 6 столбец таблицы 5. Для того, чтобы заполнить 6 столбец в уравнение тренда у = 90,58 вместо t подставим значения из 1 столбца. В 7 столбец занесем разность между 2 и 6 столбцами. И, наконец, в 8 столбец занесем отношение 7 столбца ко 2, взятое по модулю, и это число умножим на 100%. Учитывая среднее значение, получим, что . Заметим, что все три показателя находятся в пределах нормы, значит, модель тренда соответствует реальности.

Теперь мы можем продолжить заполнение таблицы 4.

5 столбец совпадает с 6 столбцом таблицы 5.

6 столбец получаем, перемножая значения 3 столбца и 5 столбца таблицы 4.

7 столбец получаем как отношение второго столбца к 6, он показывает ошибку в мультипликативной модели.

8 столбец рассчитываем, как разность 2 и 6 столбцов. Эти значения дают нам абсолютную ошибку.

9 столбец служит для сравнения мультипликативной модели с другими моделями временного ряда. Возводя в квадрат значения 7 столбца, вычислим по аналогии с аддитивной моделью долю объясненной дисперсии (1 – 207,4/5023) = 0,959.

Следовательно, можно сказать, что мультипликативная модель объясняет 95,9% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.

Сравнение модели с исходным графиком, можно посмотреть на рисунке 2.

Рисунок 2

Спрогнозируем прибыль компании на ближайшее полугодие.

У = У₁₇ + У₁₈, где У₁₇ = Т₁₇ S₁₇, а У₁₈ = Т₁₈ S₁₈.

Заметим, что S₁₇ = 0,913, а S₁₈ = 1,209 (взяты из таблицы 3).

Т₁₇ = 90,58 , а Т₁₈ = 90,58 = 40,72

Тогда У = 0,913 + 40,721,209 =88,93685 тыс. долл. США. Значит, прогноз составляет 88936, 85 долл. США.

Обратить внимание!

• для построения моделей временного ряда необходимо минимум 8 показателей.

• при построении данных моделей не исследовалась гомоскедастичность остатков, так же как и автокорреляция уровней временного ряда, то есть выводы сделаны исходя из визуального анализа графика временного ряда.

• процесс вычислений значительно упрощается, если их производить с помощью Excel (см. Приложение 1).

• при расчетах тренда необходимо обратить внимание на его линейность. Рассмотренный в примере метод расчета тренда годится только для линейного тренда.

• при вычислении параметров тренда необходимо следить за тем, чтобы коэффициенты корреляции, детерминации и средняя ошибка аппроксимации находились в пределах нормы (коэффициент корреляции более 0,65, коэффициент детерминации более 75%, средняя ошибка аппроксимации не превосходит 7%).