Построение модели временного ряда средствами Exel 2007

Рассмотрим построение модели аддитивного ряда средствами Exel 2007 на примере изучения объемов потребления электроэнергии (млн кВТ*ч) жителями региона за 16 кварталов и на основании полученной модели спрогнозируем объем потребляемой электроэнергии на следующие полгода. Построенный пример описан в .

Пусть известный объем потребляемой электроэнергии задан таблицей 1.

Таблица 1. Потребление электроэнергии жителями региона, млн кВТ*ч

№ кварт.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Объем электроэнергии (млн кВТ*ч)	6,0	4,4	5,0	9,0	7,2	4,8	6,0	10	8,0	5,6	6,4	11	9,0	6,6	7,0	10.8

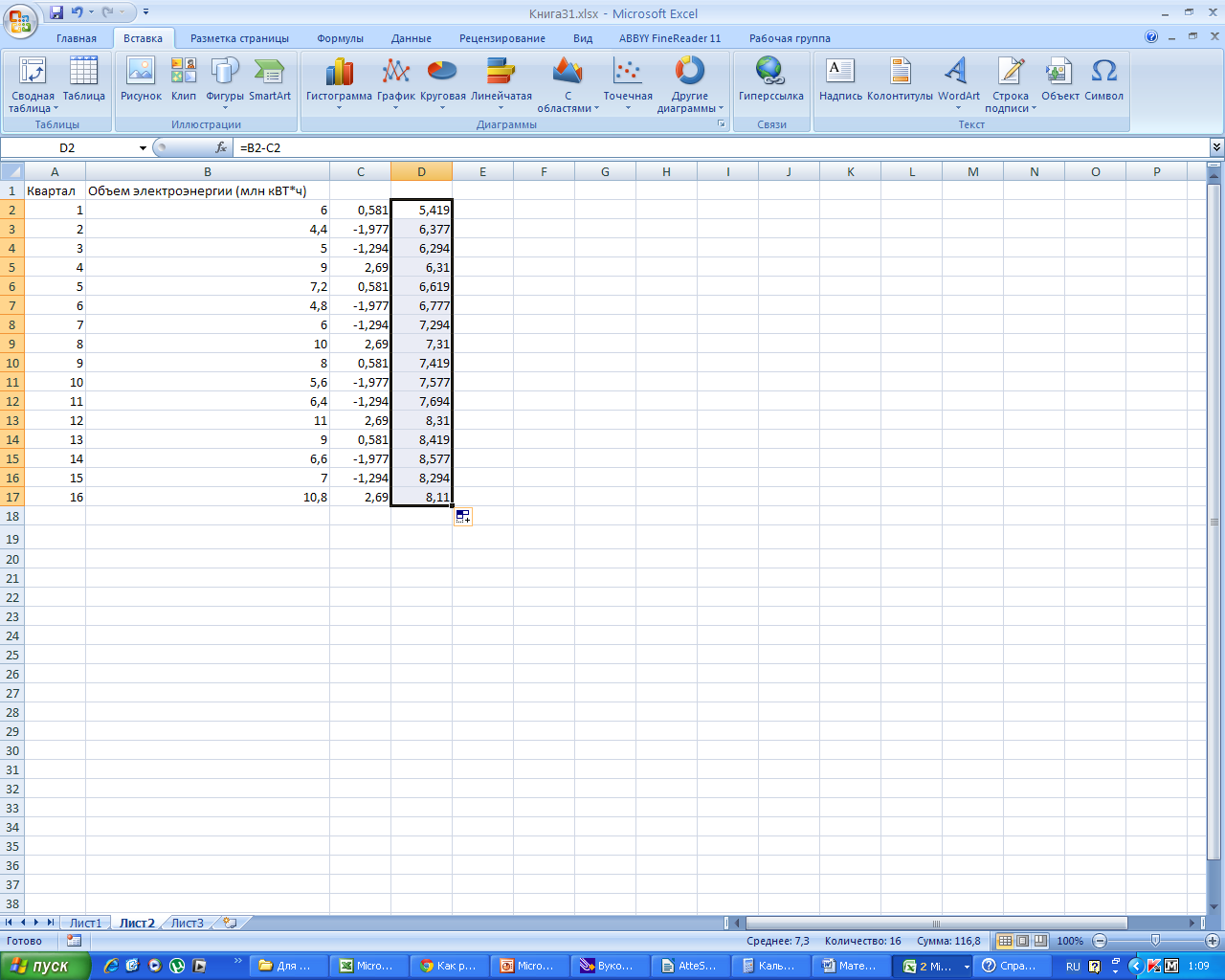
1. Внесем эти данные в таблицу

2. В главном меню выбираем «ВСТАВКА»

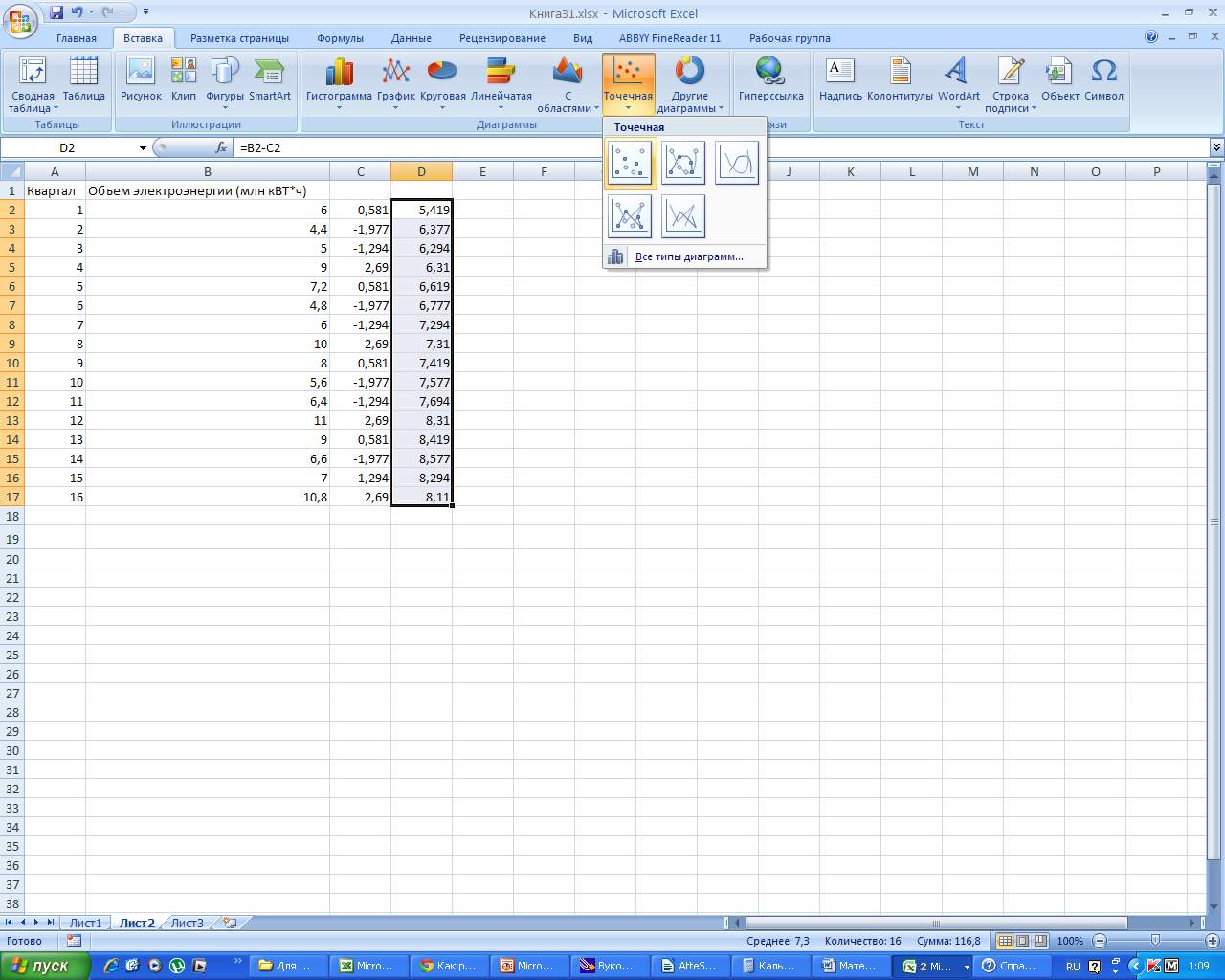
3. В главном меню выбираем «ТОЧЕЧНАЯ»

4. Получаем график

5. Теперь считаем сезонную компоненту и среднюю ошибку аппроксимации. Для этого открываем лист 2 и копируем в него первые два столбца. По методике, описанной в 1рассчитаем значения сезонной компоненты.

Таблица 1- Расчет оценок сезонной компоненты в аддитивной модели

Номер квартала	Потребление электроэнергии	Итого за четыре квартала	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	6,0	–	–	–	–
2	4,4	24,4	6,10	–	–
3	5,0	25,6	6,40	6,250	–1,250
4	9,0	26,0	6,50	6,450	2,550
5	7,2	27,0	6,75	6,625	0,575
6	4,8	28,0	7,00	6,875	–2,075
7	6,0	28,8	7,20	7,100	–1,100
8	10,0	29,6	7,40	7,300	2,700
9	8,0	30,0	7,50	7,450	0,550
10	5,6	31,0	7,75	7,625	–2,025
11	6,4	32,0	8,00	7,875	–1,475
12	11,0	33,0	8,25	8,125	2,875
13	9,0	33,6	8,40	8,325	0,675
14	6,6	33,4	8,35	8,375	–1,775
15	7,0	–	–	–	–
16	10,8	–	–	–	–

Таблица расчета оценок сезонной компоненты в аддитивной модели заполняется по следующему правилу:

1 столбец – известный номер квартала;

2 столбец – известный объем потребляемой электроэнергии(млн кВТ*ч);

3 столбец – складываем последовательно значения четырех ячеек 2 столбца и записываем их на одну клетку ниже;

4 столбец – каждое значение 3 столбца делим на 4 (период сезонных колебаний);

5 столбец – складываем последовательно значения двух ячеек 4 столбца, делим эту сумму на 2 и записываем на одну клетку ниже;

6 столбец – из элементов 2 столбца вычитаем элементы 5 столбца.

Рассчитаем значения сезонной компоненты S

Для этой цели составим следующую расчетную таблицу 3, в которую последовательно разместим данные из 6 столбца табл. 2.

Таблица 3- Расчет значений сезонной компоненты в аддитивной модели

Показатель	Год	Номер квартала
		I	II	III	IV
	1	–	–	–1,250	2,550
	2	0,575	–2,075	–1,100	2,700
	3	0,550	–2,025	–1,475	2,875
	4	0,675	–1,775	–	–
Итого за квартал		1,800	–5,875	–3,825	8,125
Средняя оценка сезонной компоненты (		0,600	–1,958	–1,275	2,708
Скорректированная сезонная компонента		0,581	–1,977	–1,294	2,690

Средняя оценка сезонной компоненты () рассчитывается как итого за квартал /3.

В аддитивных моделях с сезонной компонентой предполагается , что сезонные воздействия за период взаимопогашаются. Это означает, что сумма значений сезонной компоненты по всем кварталам должна быть равна 0.

Для данной модели имеем 0,600+ (–1,958) + (–1,275) + 2,708 = 0,075 0.

Определим корректирующий коэффициент k = 0,075/4 = 0,01875.

Рассчитаем скорректированные значения сезонной компоненты, как разность между ее средней оценкой и корректирующим коэффициентом k:

k.

Проверим условие равенства нулю суммы значений сезонной компоненты: 0,581 – 1,977 – 1,294 + 2,690 = 0.

6. Подставим значения скорректированной сезонной компоненты в столбец С.

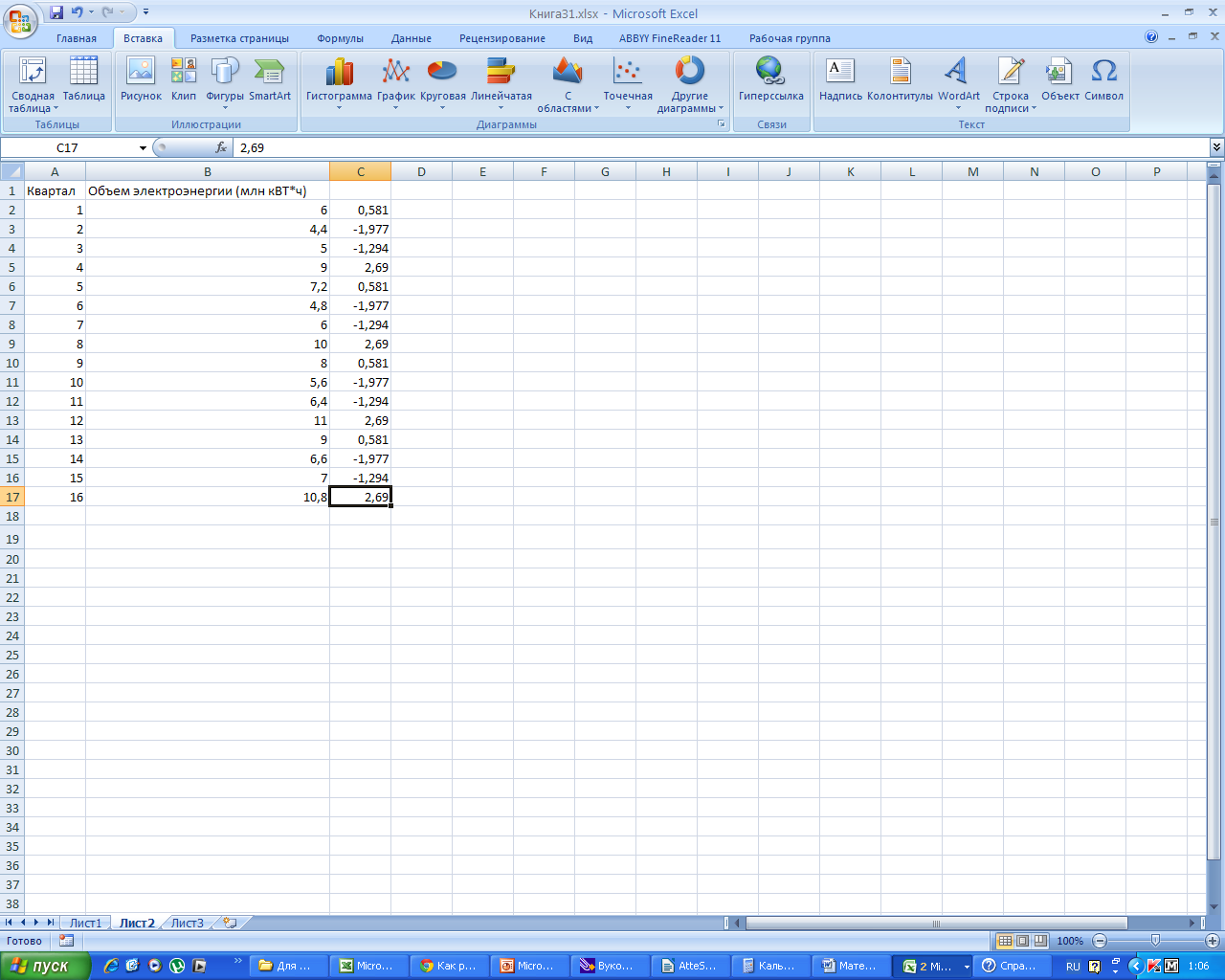
7. Заполняем столбец D, как разность В и С.

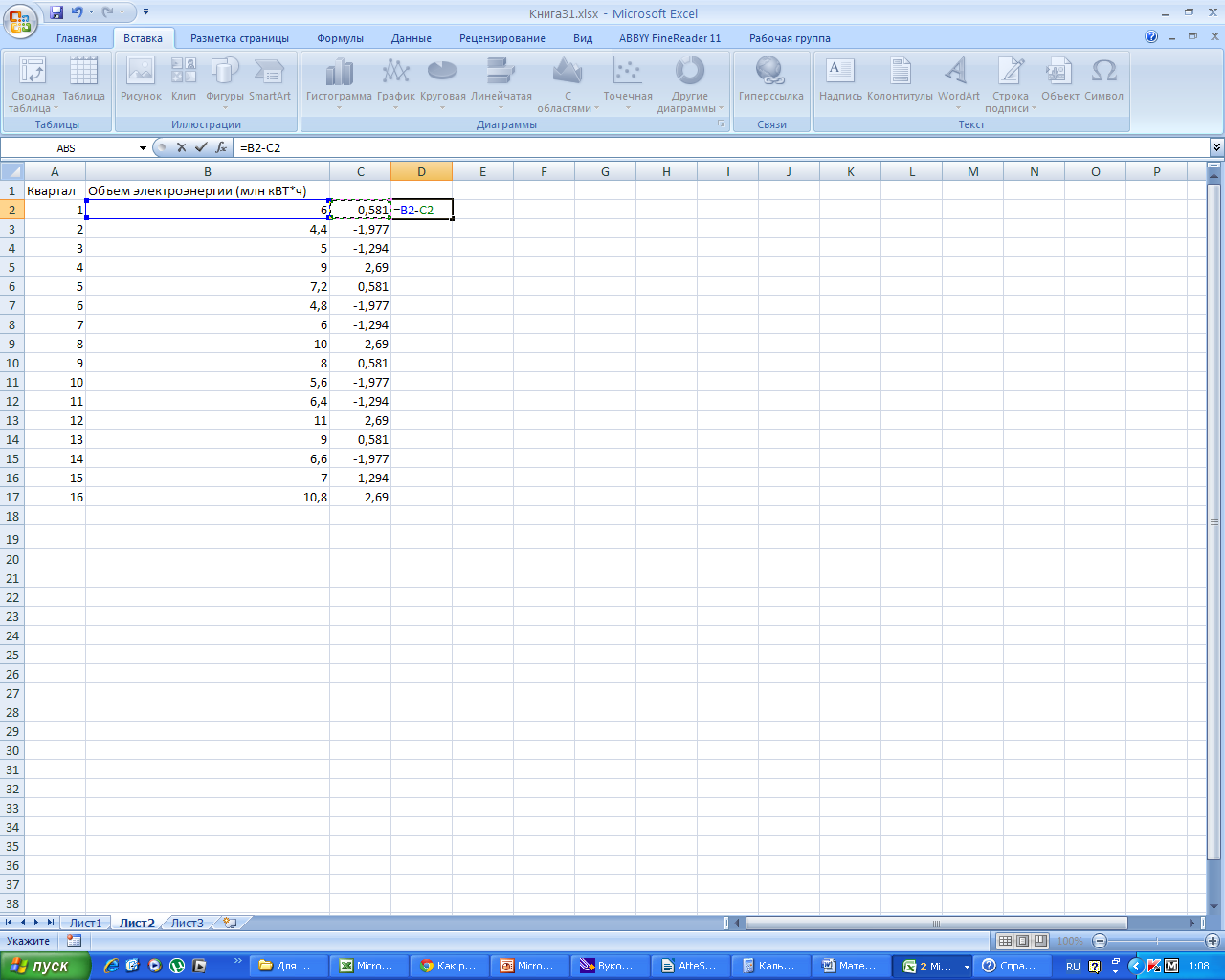
Получаем

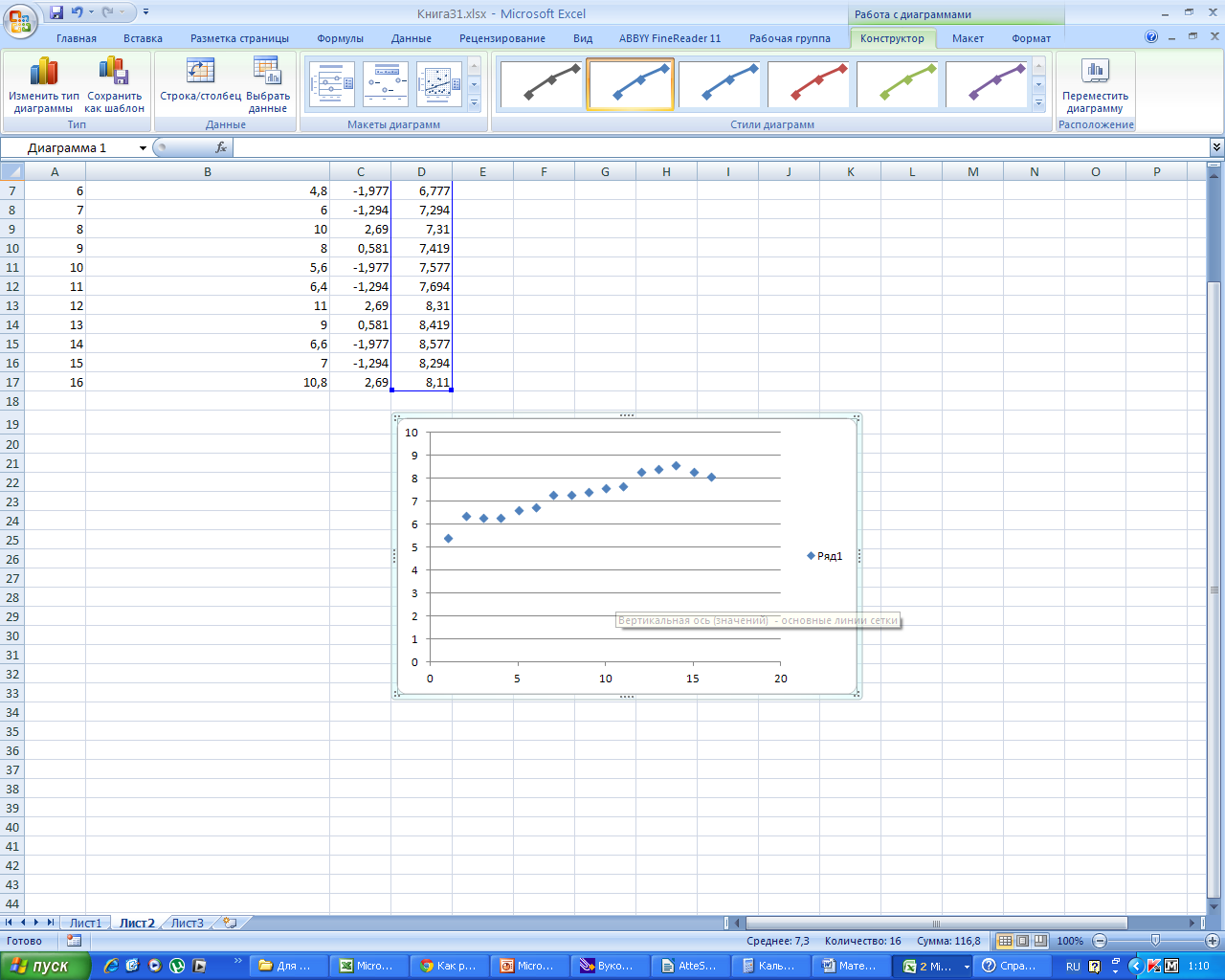
8. Пошагово выбираем ту линию тренда, где наибольшее значение имеет R².

Для этого ставим курсор на точки поля корреляции и выбираем тренд, расставляя галочки в окна, «показать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации».

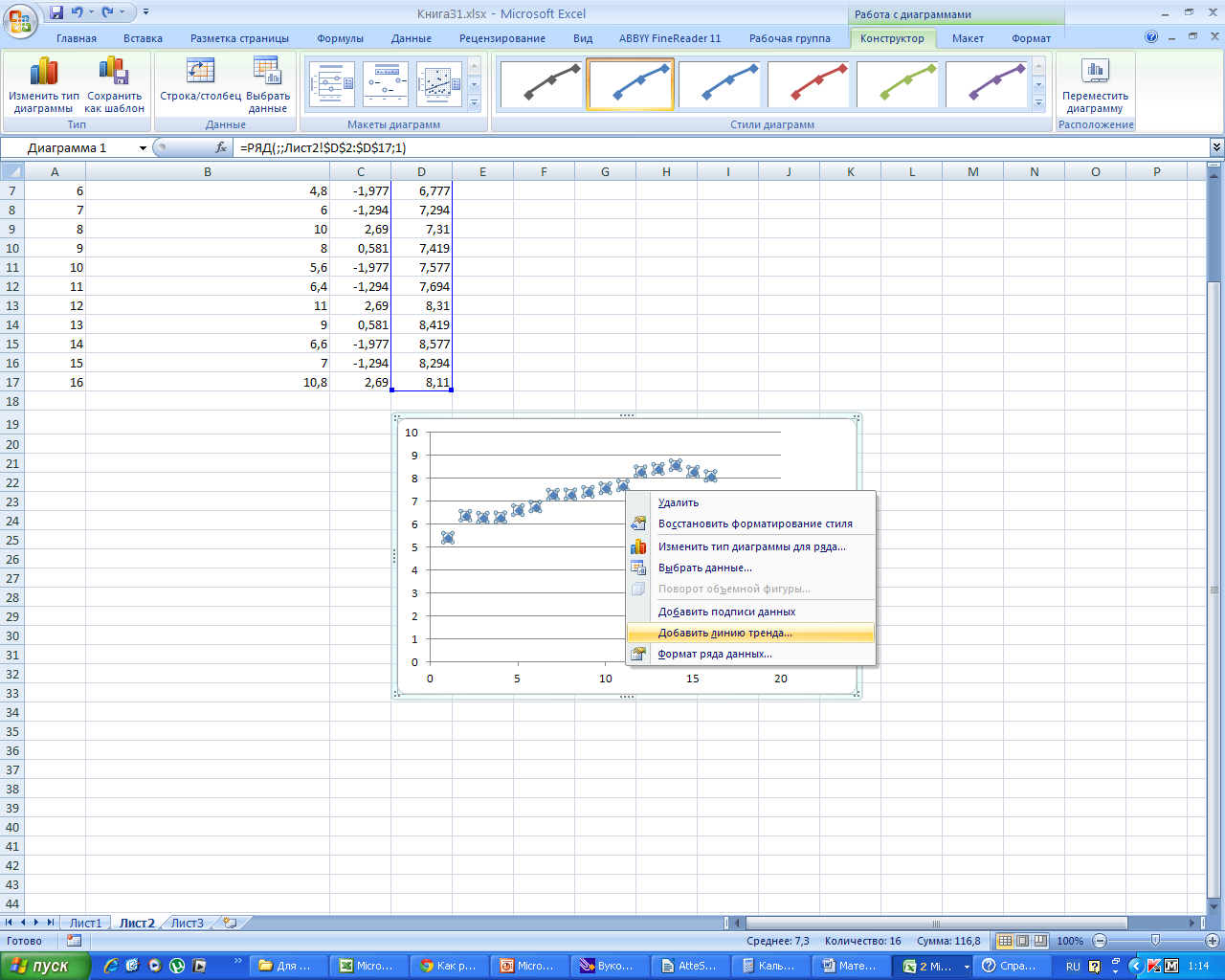
9. В столбец Е вбиваем формулу для уравнения тренда y= 0, 1864x + 5, 7155 и получаем расчетные значения для тренда.

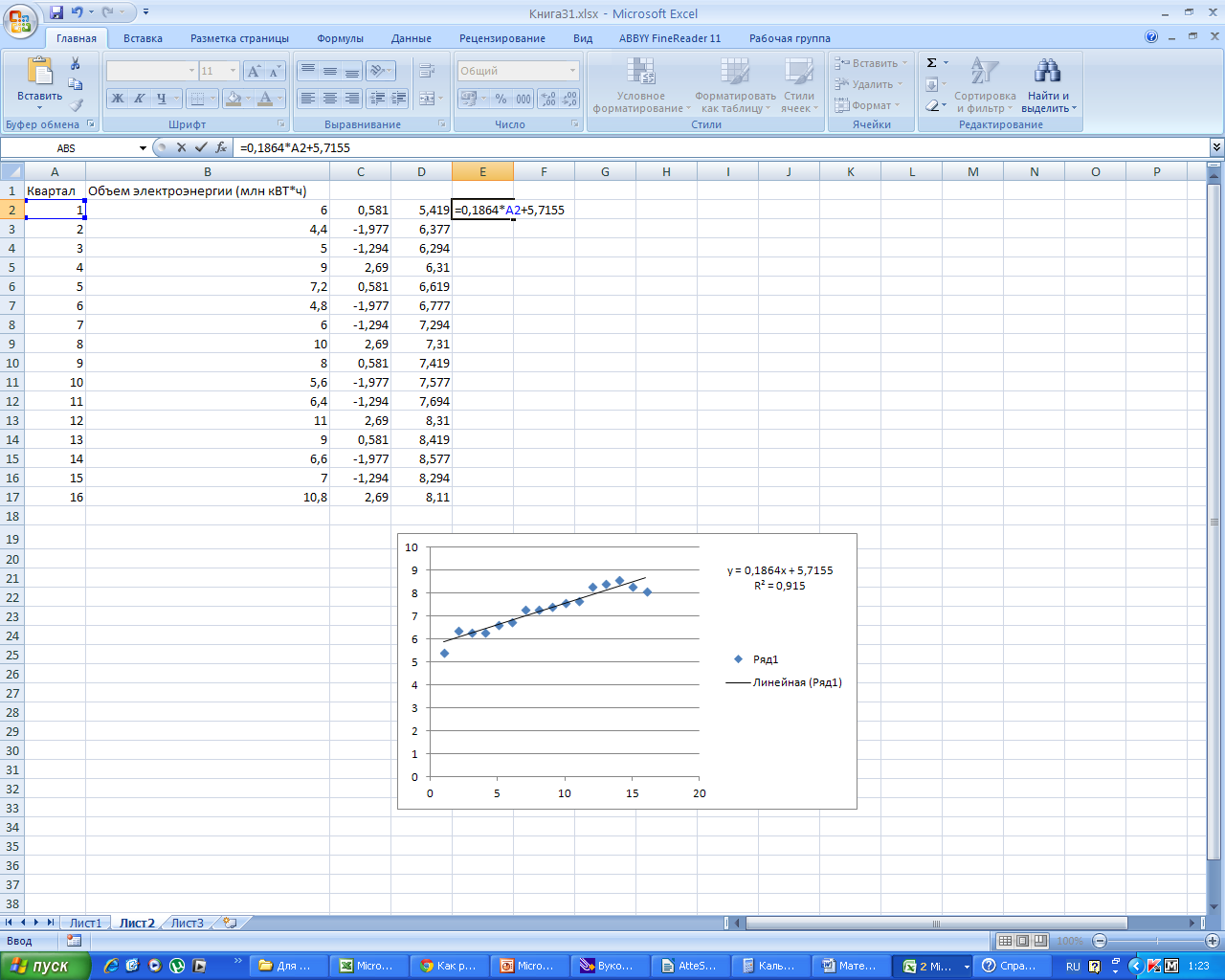
10. Заполним столбец F, как сумму C и Е, и найдем ошибку аппроксимации.

Для нахождения ошибки аппроксимации заполним столбец G. Для этого в столбец G вставляем формулу

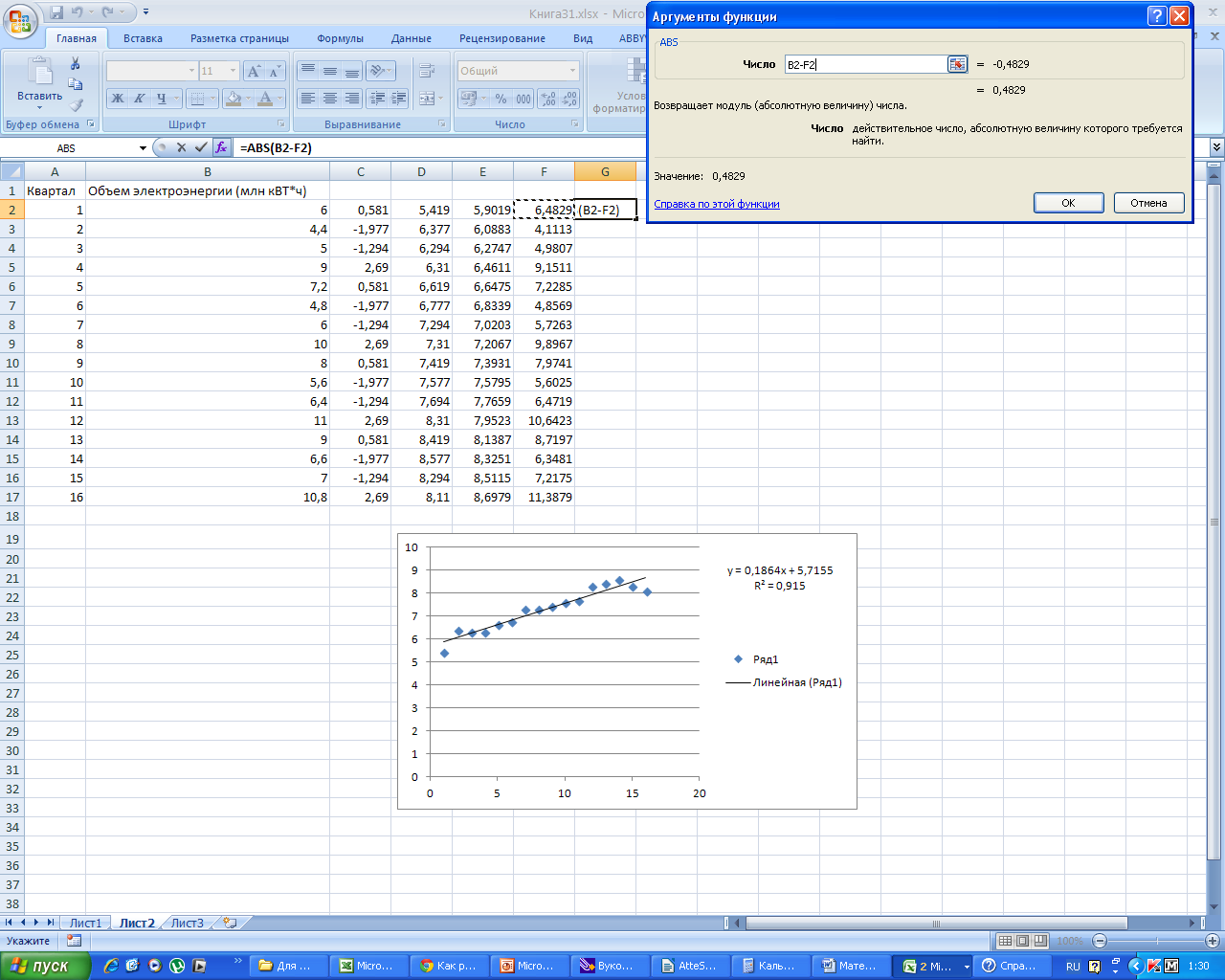
Получаем

Найдем среднюю ошибку аппроксимации, заполнив столбец Н. Для этого разделим G на В и умножим на 100%.

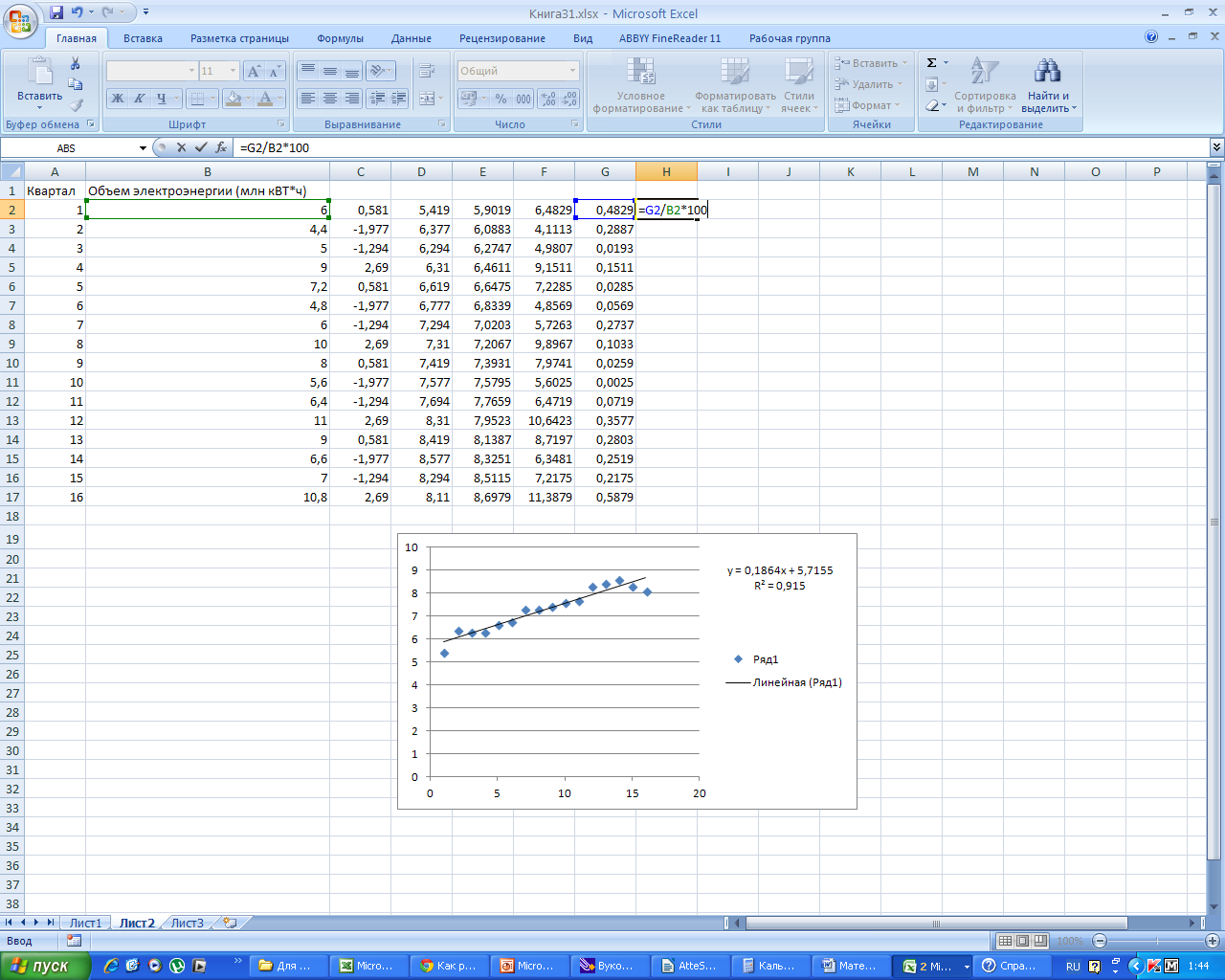
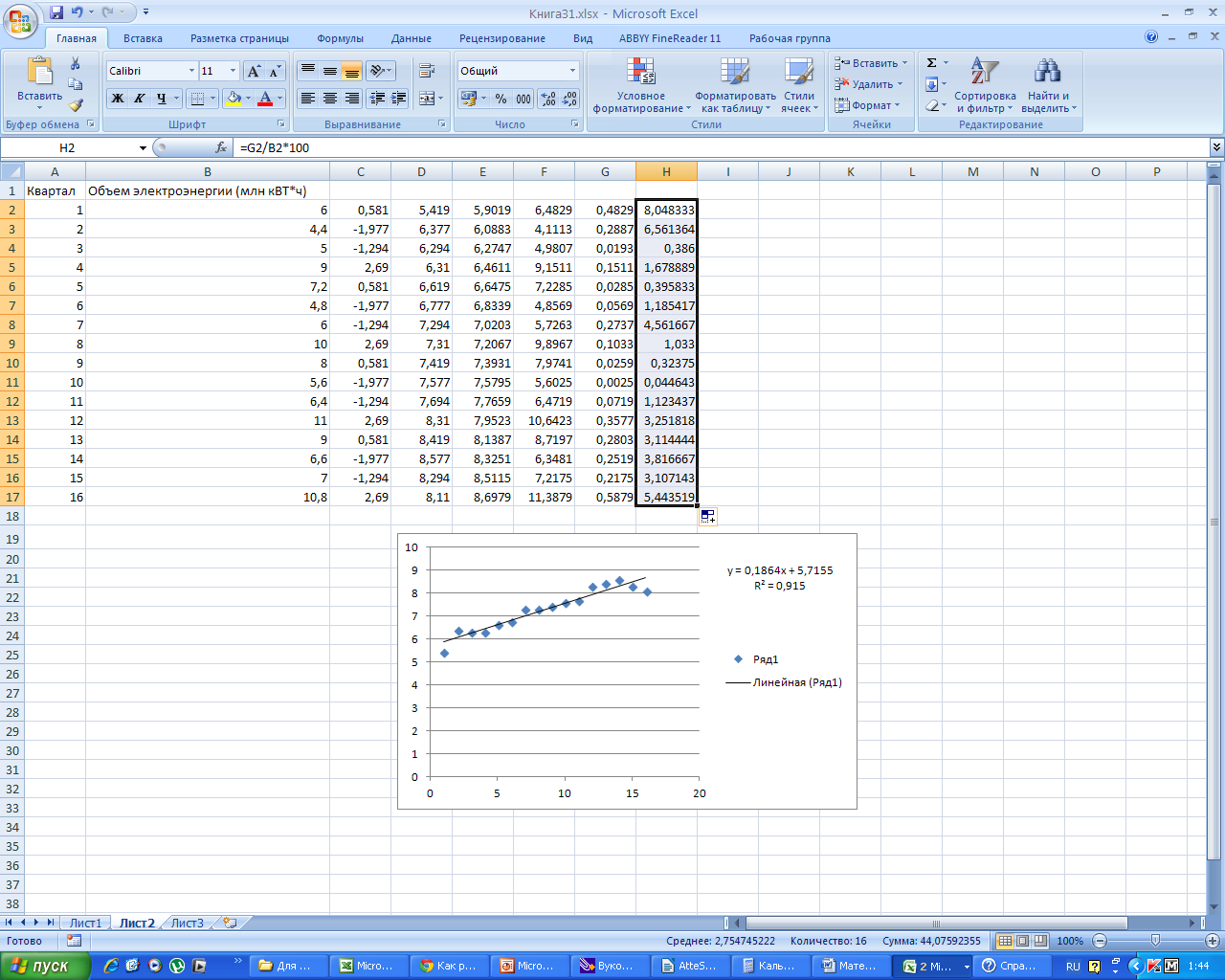
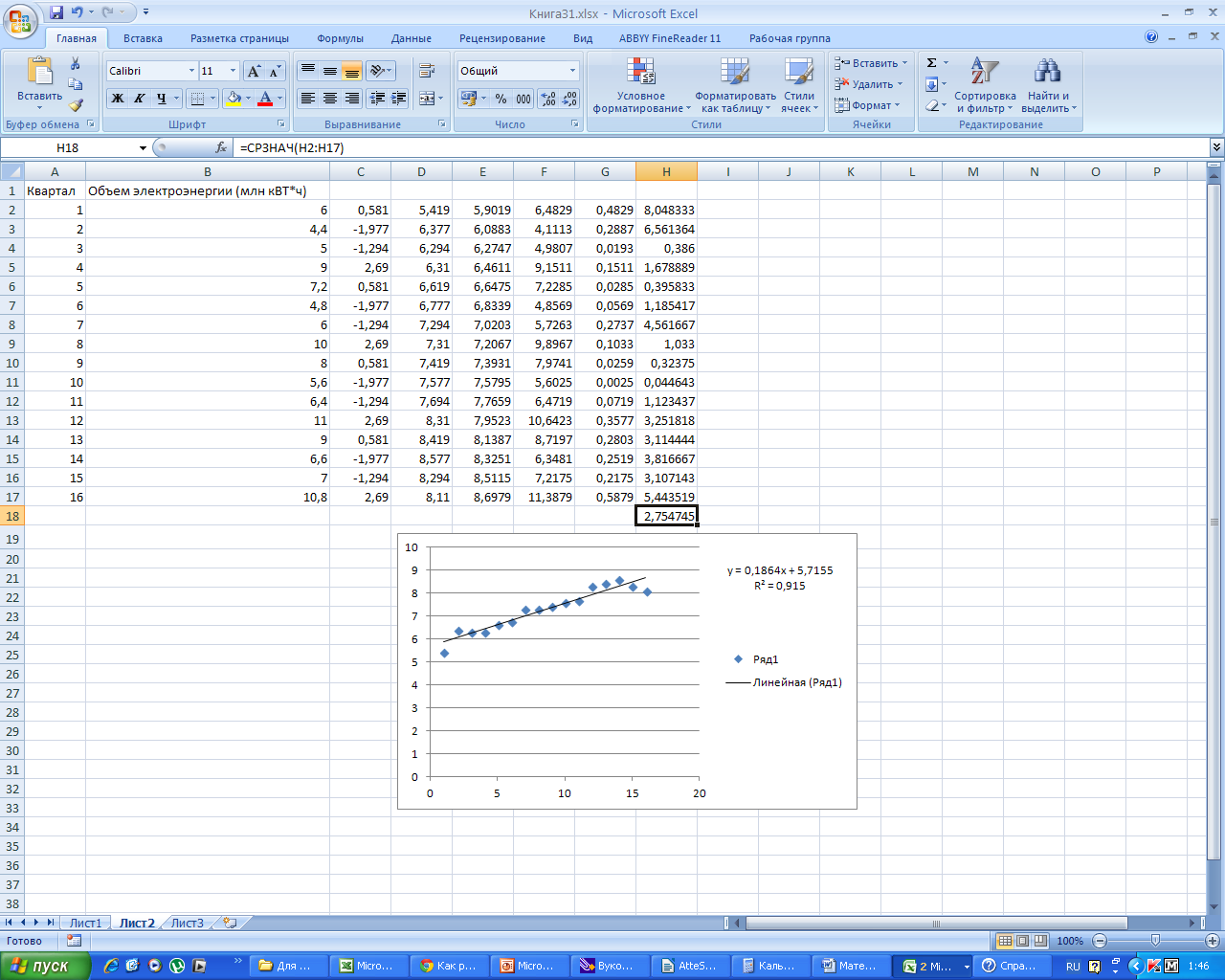
Таким образом, заметим, что R² = 0,915 0,75, средняя ошибка аппроксимации равна 2,75%< 3%. Значит, данная модель является надежной.

Спрогнозируем значения потребляемой электроэнергии на следующий квартал. Для этого воспользуемся вновь электронной таблицей.

Заметим, что полученное число 8,8843 млн. кВт/ч. практически не отличается от полученного ранее значения млн. кВт/ч.

Приложение 2.