
Набор учебников PDF Хороший солдат / Физика / Физика. Механика
.pdfВведение |
11 |
ных задач. Последнее способствует запоминанию физических законов и более глубокому осознанию их сущности, позволяет натренироваться в применении физических формул и математических преобразований. При решении физических задач руководствуйтесь следующим:
—внимательно изучите условие задачи, пытаясь понять физическую сущность явлений и процессов, рассматриваемых в ней, уясните основной вопрос задачи;
—выделите заданные и неизвестные величины, кратко запишите условия задачи, переведите значения необходимых величин в систему СИ;
—сделайте рисунок, схему или чертеж, указав все необходимые величины;
—установите физические закономерности, позволяющие описать рассматриваемую в задаче ситуацию, и запишите их в математической форме;
—введите удобную систему координат;
—запишите уравнение или систему уравнений, связывающих известные и неизвестные параметры задачи;
—найдите искомые величины в общем виде, проведя необходимые алгебраические преобразования;
—проверьте правильность решения с помощью размерностей физических величин — с правой и с левой сторон равенства должны получаться одинаковые размерности;
—подставьте в общее решение числовые значения величин и произведите расчеты с учетом правил приближенных вычислений;
—оцените правильность полученного результата;
—запишите ответ в единицах системы СИ (или в тех единицах, которые в большей степени соответствуют смыслу задачи).
Для того чтобы успешно сдать экзамен по физике, студенту недостаточно иметь хорошую теоретическую подготовку и уметь решать физические задачи. Часто причина неудачи — слабые математические навыки, отсутствие внимательности, аккуратности и собранности.
Укажем на некоторые недостатки, встречающиеся на экзаменах по физике:
—формализм знаний, нечеткое и поверхностное понимание физических законов;
12 |
Введение |
—неправильное понимание условия задачи;
—проявление невнимательности при краткой записи условия задачи (использование отсутствующих физических параметров или неправильное толкование имеющихся);
—отсутствие навыков перевода физических величин из одних единиц в другие;
—незнание основ дифференциального исчисления и элементарных правил векторной алгебры;
—неумение проводить алгебраические преобразования и арифметические вычисления, решать квадратные уравнения, работать с показателями степеней и т. д.;
—некритическое отношение к результатам, неумение выбирать из полученных решений правильные ответы, соответствующие физическим условиям задачи.
В пособии принята сквозная нумерация формул, рисунков, примеров решения задач, тестов и контрольных задач. Первое число соответствует номеру главы, второе число — порядковому номеру формулы, рисунка и т. д.
Для работы с книгой помимо владения алгеброй и тригонометрией необходимо знакомство с элементами дифференциального и интегрального исчисления, а также векторной алгебры. Если же студент обладает недостаточными математическими навыками, то начать работу с книгой следует с математического введения. Помните, что изучить физику за несколько недель невозможно. Для успешного овладения и, что самое главное, возможности применения физических идей при дальнейшем обучении и в профессиональной деятельности необходима регулярная, повседневная работа — длительные размышления над изучаемыми проблемами.
Авторы надеются, что изучение материалов пособия окажет заинтересованным студентам большую помощь в овладении курсом физики, создаст у них определенное представление об уровне экзаменационных требований и будет способствовать дальнейшему успешному обучению в вузе.

МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ
1. ВЕКТОРНАЯ АЛГЕБРА
Вектором называется направленный отрезок, для которого заданы длина, называемая модулем или величиной вектора, и направление. Скалярной величиной, или скаляром, называется число, то есть величина, неG обладающая направлением.
Сила F, действующая на материальную точку, есть вектор, так как она обладает направлением. В курсе физикиGвы познакомитесьG
с такими векторными величинами,G как скоростьG v, ускорение a, импульс pG, момент импульсаG L, момент силыGM , напряженность электрического поля E, магнитная индукция B и т. д.
Температура тела T есть скаляр, так как с этой числовой величиной не связано никакое направление. Масса тела m и его плотность
ρ — тоже скаляры.
Над векторами производят действия, называемые сложением, вычитанием и умножением векторов.
1.1. СЛОЖЕНИЕ ВЕКТОРОВ
Если заданы векторы aG и bG, то их можно сложить по правилам
параллелограмма или треугольника (рис. 1.1 и рис. 1.2 соответствен- |
||||
но). Вектор cG |
является их суммой: |
G |
|
|
|
G |
G |
(1.1) |
|
|
c = |
a + |
b . |
|
Рис. 1.1 |
Рис. 1.2 |

14 |
|
|
|
|
МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ |
|
Y |
|
|
|
В первом случае суммарный век- |
|
bGy |
|
G |
|
тор cG представляет собой диагональ |
by |
|
b |
|
параллелограмма, построенного на |
|
|
|
|
cG |
|
составляющих векторах как на сто- |
cy |
G |
aG |
|
ронах (начала всех трех векторов |
|
ay |
|
|
совпадают). Во втором случае по- |
||
y |
|
|
|||
|
|
|
|
|
ступают так: с концом вектора aG |
|
|
|
|
|
совмещают начало вектора bG. Со- |
|
|
G |
G |
|
единив затем начало первого векто- |
|
|
|
ра с концом второго, получают сум- |
||
|
|
ax |
bx |
|
G |
O |
|
ax |
bx |
X |
марный вектор c. |
|
Составляющей вектора вдоль пря- |
||||
|
|
|
cx |
|
мой (плоскости) называется век- |
|
|
Рис. 1.3 |
|
|
тор, лежащий на данной прямой |
|
|
|
|
|
(плоскости), начало и конец которогоG G совпадают с проекциями началаGи концаG вектораG . На рис. 1.3 ax и аy —G это составляющие вектора a, а bx и by — составляющие вектора b. Проекцией вектора на ось называется скаляр (число), равный по величине модулю составляющей вектора на ту же ось, причем это число берется со знаком плюс, если направление составляющей вектора совпадает с направлением оси, и со знаком минус, если эти направления противоположны. Проекции суммарного вектора на координатные оси равны сумме проекций слагаемых векторов
сx = ax + bx, сy = ay + by. |
(1.2) |
Это видно из рисунка 1.3.
1.2. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
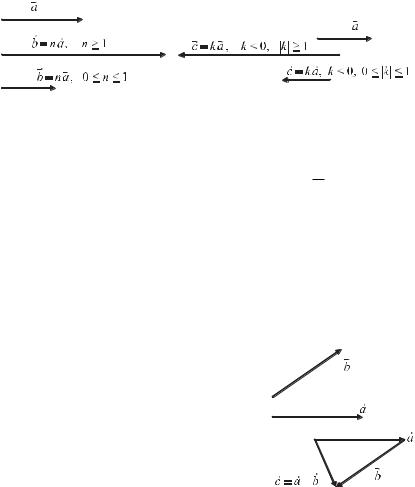
Пусть требуется умножить вектор aG на число n. Если число n положительное,G то в результате умножения получится новый вектор b = n aG, имеющий то же направление, что и вектор aG, но модуль в n раз больший, если n ≥ 1, и модульG в 1/n раз меньший, если 0 ≤ n ≤ 1 (рис. 1.4). Модуль вектора b равен b = | n | a, а проекция вектора b равна bx = nax.
1. Векторная алгебра |
15 |
Рис. 1.4 |
Рис. 1.5 |
Если вектор GумножитьG на отрицательное число k (k < 0), то поG - лучится вектор c = k a, направленный противоположно вектору a, с
модулем в |k | раз большим, если |k| ≥ 1, и модулем в |1k| раз меньшим,
если 0 ≤ |kG| ≤ 1 (рис. 1.5). Модуль вектора cG равен с = |k |a, а проекция вектора c равна сx = kax.
1.3. ВЫЧИТАНИЕ ВЕКТОРОВ |
|
|
|
||||
Вычесть из вектора |
aG вектор bG(рис. 1.6) — значит прибавить к |
||||||
вектору aG вектор (−bG) |
, отличающийся от вектора bG |
тем, что он на- |
|||||
правлен в противоположную сторону (знак |
|
|
|
||||
минус указывает здесь противоположность |
|
|
|
||||
направления): cG = aG – bG= aG+ ( |
−bG) . |
|
|
|
|||
Модули векторов bG |
и (−bG) равны, а их |
|
|
|
|||
направления противоположны (такие век- |
|
|
|
||||
торы называются противоположными). |
|
|
|
||||
Проекции противоположных векторов име- |
|
|
|
||||
ют противоположные знаки. Сами же век- |
|
|
|
||||
торы не могут быть ни положительными, ни |
|
|
|
|
|
||
|
|
|
|||||
|
|
|
|
||||
отрицательными. |
|
|
|
|
Рис. 1.6 |
||
Можно находить разность векторов ина- |
|||||||
|
G |
G |
|
|
|
||
че. Если представить векторы a |
и b выходящими из одной точки |
||||||
(рис. 1.7), то разность векторов изобразитсяG вектором сG, проведенным из концаG «вычитаемого» вектора b к концу «уменьшаемого» вектора a .

16 |
МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ |
Рис. 1.7
Рис. 1.8
Рис. 1.9
При вычитании векторов вычитаются и их проекцииGна координат-
ные оси. Если cG = aG− b , то сx = ax – bx (рис. 1.8).
1.4. КООРДИНАТЫ ВЕКТОРА
ПрямоугольнымиG координатами вектораG a называются проекции вектора a на оси координат (рис. 1.9). Координаты вектора обозначаются буквами ax, ay, az.
Запись:
aG= {ax, ay, az}. |
(1.3) |
|
Векторы iG , |
Gj , kG , изображенные |
|
на рисунке, называются единичными ортами (единичными векторами) координатных осей. Их модули равны единице, а направления совпадают с направлением осейGОX, ОY и ОZ. Зная проекции вектора a, можно представить его как
aG = ax iG + ay Gj + az kG . (1.4)
1.5. ДЛИНА ВЕКТОРА
Длина вектора cG = {сx, сy, сz} выражается через его координаты по теореме Пифагора формулой
| cG | = cx2 + cy2 + cz2 . |
(1.5) |
G G GПосле нахождения вектора c , являющегося суммой векторов Ga
и b, в физике часто возникает задача нахождения модуля вектора c, т. е. его длины. Возможны следующие случаи:

1. Векторная алгебра |
17 |
1. Складываемые векторы сонаправлены (aG ↑↑ b). В этом случае от векторной записи
G |
G |
G |
(1.6) |
c = |
a |
+ b |
|
|
|
|
легко перейти к скалярной, |
|
|
|
спроектировав уравнение |
|
|
|
(1.6) на ось OX (рис. 1.10) |
Рис. 1.10
Рис. 1.11
OX: с = a + b. (1.7)
2. Складываемые векторы противоположноG направлены (aG ↑↓ b). СпроектироG - вав уравнение cG = aG + b на ось OX (рис. 1.11), получаем
OX: –с = a – b. (1.8)
3. Складываемые векторы перпендикуляр- |
|
||
ны (рис. 1.12). Модуль вектора cG |
находим по |
|
|
теореме Пифагора, записанной для прямо- |
|
||
угольного треугольника ODE. ОD = bG |
и |
|
|
DЕ = aG — катеты треугольника, ОЕ = |
|
||
cG — его гипотенуза. Поэтому |
|
|
Рис. 1.12 |
cG = |
a2 + b2 |
. |
(1.9) |
4. Угол α между складываемыми |
|
|
|
векторами произвольный (рис. 1.13) |
|
|
|
(α не равен 0°, 90°, 180°, как это име- |
|
|
|
ло место выше). В этом случае при- |
|
|
|
меняется теорема косинусов: Квадрат |
|
|
|
одной стороны треугольника равен сум- |
|
|
|
ме квадратов двух других сторон ми- |
|
Рис. 1.13 |
|
нус удвоенное произведение сторон на
косинус угла между нимиG . Для треугольника ODE, в котором известны стороны ОD = b и DЕ = aG , а также угол α, теорема запишется как
с2 = а2 + b2 − 2 а b cosα. |
(1.10) |

18 |
МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ |
Применяя теорему косинусов, следует помнить,Gчто в ней идет речь не об угле между складываемыми векторами aG и b (угле β), а об угле α = 180° − β. Так как cos (180° − β) = −cosβ, выражение (1.10) можно записать в следующем виде:
|
с2 = а2 + b2 + 2 а b cosβ. |
|
|
|
(1.10) |
||
1.6. УГЛЫ МЕЖДУ ОСЯМИ КООРДИНАТ И ВЕКТОРОМ |
|
||||||
|
Углы α, β, γ, образуемые положитель- |
||||||
|
ными направлениями OX, OY, OZ с век- |
||||||
|
тором aG |
= {ax, ay, az} (рис. 1.14), можно |
|||||
|
найти по формулам |
|
|
|
|
||
|
cosα = |
ax |
= |
aGx |
, |
(1.11) |
|
|
|
ax2 + ay2 + az2 |
|
|a | |
|
|
|
|
cosβ = |
a |
|
= |
a |
, |
(1.12) |
|
|
y |
Gy |
||||
|
|
ax2 + ay2 + az2 |
|
|a | |
|
|
|
Рис. 1.14 |
cosγ = |
az |
= |
aGz |
. |
(1.13) |
|
|
|
ax2 + ay2 + az2 |
|
|a | |
|
|
|
Вопросы и задания для самопроверки
1.Дайте определение вектора, скалярной величины.
2.Среди перечисленных физических величин выберите векторные и скалярные: скорость, сила, путь, масса, перемещение, температура, ускорение, плотность, давление, электроемкость, импульс, влажность.
3.В чем заключаются правила параллелограмма и треугольника,
применяемые для сложения векторов? G
4. В каком случаеG при умножении вектора a на число результирующий вектор b сонаправлен с вектором aG? Противоположно направлен?
5.Как вычесть из вектора aG вектор b?
6.Что такое орты координатных осей? Как представить вектор через его проекции на координатные оси и орты координатных осей?G

1. Векторная алгебра |
19 |
7.Как найти длину вектора a, зная его проекции ax, ay, az на координатные оси?
8.Как найти угол между осью координат и вектором?
9.Сформулируйте теорему косинусов.
Примеры решения задач
Задача 1.1
Самолет держит курс на север со скоростью v1 = 200 м/с относительно Земли. Дует восточный ветер со скоростью относительно Земли v2 = 15 м/с. Найти скорость самолета v относительно воздуха.
|
Дано: v1 = 200 м/с; v2 = 15 м/с. |
|
|
|
|
|||
|
Найти: v. |
|
|
|
|
|
|
|
vG |
Скорость самолета относительно воздуха vG |
равна |
||||||
= vG |
− vG |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
Изобразим треугольник скоростей. |
|
|
|
|
|||
|
|
|
|
|
||||
|
Так как vG |
vG , модуль искомой скорости находим |
||||||
|
|
1 |
2 |
|
|
|
|
|
по теореме Пифагора: v = v2 |
+ v2 = 2002 |
+ 152 |
= 200,56 м/с. |
|||||
|
|
|
1 |
2 |
|
|
|
|
Ответ: скорость самолета относительно воздуха v = 200,56 м/с.
Задача 1.2
Найти модуль напряженности Е поля двух точечных зарядов q1 = 1 нКл и q2 = 2 q1 в точке, находящейся на середине соединяющего их отрезка длиной r = 1 м.
Дано: q1 = 1 нКл; q2 = 2 q1; r = 1 м.
Найти: Е. G G G G G Согласно принципу суперпозиции полей E = E1 + E2 , где E1 и E2 −
напряженности полей зарядов q1 и q2 в точке А. Спроектируем это уравнение на ось ОX.
OX: Еx = Е1 − Е2.

20 |
МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ |
Знак «−» говорит о том, что вектор EG направлен противоположно оси ОX. Подставим числовые значения
Тогда Е =| Еx | = 


Ответ: модуль напряженности поля двух точечных зарядов
Е = 


Задача 1.3 G G
К телу приложены силы F1 и F2 , угол между которыми β = 20°. НайG- ти модуль результирующей силы F, действующей на тело, если F1 = F2 =
20 Н. Дано: β = 20°; F1 = 20 Н; F2 = 20 Н. Найти: F. G
РезультирующаяG G силаG FG, действующаяG на тело, — это векторнаяG G сумма сил F1 и F2 : F = F1 + F2 . Найдем сумму векторов F1 и F2 по правилу параллелограмма (см. с. 13). Для треугольника сил ОДЕ (ОД = F2, ДЕ = F1, ОЕ = F ) запишем теорему косинусов:
ОЕ 2 = ОД 2 + ДЕ 2 − 2 ОД ДЕ cosα
или
F2 = F12 + F22 − 2 F1 F2 cosα,
где α = 180° − β.
Так как по условию F1 = F2, то 












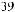

 . Ответ: модуль результирующей силы F ≈ 39,4 H.
. Ответ: модуль результирующей силы F ≈ 39,4 H.
