
Набор учебников PDF Хороший солдат / Физика / Физика. Механика
.pdfТесты для электронного экзамена |
221 |
Теорема об изменении кинетической энергии (импульс)
Т3.46 Если для двух автомобилей массами 2 т и 1,2 т, двигающихся по горизонтальному пути, отношение тормозных путей 1,7, то от-
ношение их импульсов в начале торможения равно |
|
|||
1) 1,96 |
2) 2,17 |
3) 1,41 |
4) 1,62 |
5) 1,84 |
Т3.47 Если двигатели ракеты массой 10 т совершат 7,2 · 107 Дж работы на каждый 1 кг ее массы, то импульс ракеты станет равным
1) 12 · 107 кг · м/с |
2) |
107 кг · м/с |
3) 1,5 · 107 кг · м/с |
4) 0,8 · 108 кг · м/с |
5) |
36 · 107 кг · м/с |
|
Закон изменения и сохранения импульса
Т3.48 Если тело массой 0,28 кг, движущееся со скоростью 318 м/с, распадается на два осколка с импульсами, модули которых 64,2 кг·м/с
и 48,4 кг · м/с, то угол между этими импульсами равен |
|
|||
1) 45° |
2) 52,4° |
3) 76,4° |
4) 66,8° |
5) 85,5° |
Т3.49 Если от астероида отделяется тело в направлении, противоположном его движению, то при отношении изменения скорости астероида к скорости тела относительно астероида 3 · 10–7, отношение их масс равно
1) 6,1 ·103 |
2) 5 ·104 |
3) 4,5 |
·105 |
4) 3,3 ·106 |
5) 3 ·107 |
Т3.50 Если стоящий на льду |
конькобежец массой 68 кг бросает |
||||
вдоль плоскости льда камень массой 0,35 кг, который проходит до остановки 36 м, то при начальной скорости человека сразу после бро-
ска 0,12 м/с, время движения камня равно |
|
|||
1) 2 с |
2) 3 с |
3) 3,5 с |
4) 1,5 с |
5) 4,5 с |
Т3.51 Если материальная точка массой 0,8 кг, двигаясь равномерно по окружности радиусом 1,8 м, описывает четверть окружности за
3 с, то модуль изменения ее импульса за это время равен |
|
||
1) 0,39 кг · м/с |
2) 0,43 кг · м/с |
3) 1,23 кг · м/с |
|
4) 0,67 кг · м/с |
5) 0,25 кг · м/с |
|
|
Т3.52 Если мяч массой 860 г движется со скоростью 18 |
м/с под уг- |
||
лом 42° к плоскости, то после упругого с ней столкновения измене-
ние его импульса равно |
|
||
1) 40 кг · м/с |
2) |
34,2 кг · м/с |
3) 21 кг · м/с |
4) 19,4 кг · м/с |
5) |
25 кг · м/с |
|

222 Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ
Т3.53 Если автомат выпускает 580 пуль за минуту массой 5 г каждая, то при средней силе отдачи при стрельбе 32 Н начальная ско-
рость пуль равна |
|
|
|
1) 407 м/с |
2) 582 м/с 3) 524 м/с |
4) 662 м/с |
5) 740 м/с |
Т3.54 Если вагон массой 72 т сталкивается с неподвижной платформой массой 23,2 т, которая после этого начинает двигаться со скоростью 0,48 м/с, а вагон продолжает движение со скоростью 0,12 м/с, то скорость вагона до столкновения равна 1) 0,05 м/с 2) 0,28 м/с 3) 0,13 м/с 4) 0,15 м/с 5) 0,08 м/с
Т3.55 Если пуля массой 5 г, летящая горизонтально со скоростью 680 м/с, попадает в небольшое тело массой 45 г, находящееся на краю стола высотой 80 см, и застревает в нем, то расстояние по горизонта-
ли от стола до места падения тела равно |
|
|
||
1) 13,5 м |
2) 27,2 м |
3) 16,3 м |
4) 18 м |
5) 36 м |
Т3.56 |
Если два тела с отношением масс 0,34 начинают одновре- |
|||
менно соскальзывать без трения с двух горок с одинаковой высоты так, что их начальные скорости лежат в одной плоскости, то отношение высоты, на которую поднимаются тела после абсолютно неупругого удара, к высоте, с которой тела соскальзывают, равно 1) 0,4 2) 0,24 3) 0,3 4) 0,17 5) 0,8
Абсолютно неупругий удар
Т3.57 Если два точечных тела массами 0,1 кг и 0,2 кг движутся вдоль оси Ох так, что их координаты со временем изменяются следующим образом: x1 (t) = 2t − 2 (м) и x2 (t) = −t + 4 (м), то после абсолютно неупругого столкновения импульс образовавшегося тела равен
1) 0 кг · м/с |
2) |
0,1 кг · м/с |
3) 0,2 кг · м/с |
4) 0,5 кг · м/с |
5) |
1 кг · м/с |
|
Т3.58 Если два тела массами 0,2 кг и 0,25 кг движутся вдоль прямой навстречу друг другу со скоростями 0,3 м/с и 0,35 м/с, то после центрального абсолютно неупругого столкновения импульс образо-
вавшегося тела равен |
|
|
|
1) 2,75 · 10–2 кг · м/с |
2) |
10–2 кг · м/с |
3) 1,5 · 10–2 кг · м/с |
4) 0,8 · 10–2 кг · м/с |
5) |
6,3 · 102 кг · км/ч |
|
Задачи для контрольных работ |
223 |
Абсолютно упругий удар
Т3.59 Если два точечных тела массами 0,4 кг и 0,25 кг движутся вдоль оси Ох так, что их координаты со временем изменяются следующим образом: x1 (t) = 3t (м) и x2 (t) = −2t + 8 (м), то после абсолютно упругого столкновения отношение скорости второго тела к ско-
рости первого равно |
|
|
|
|
1) 1,7 |
2) 0 |
3) 1,45 |
4) 2,8 |
5) 5 |
Т3.60 Если два тела массами 0,63 кг и 0,27G кг движутсяGвдоль оси Ох навстречу друг другу со скоростями 3, 2i (м/с) и −4,8i (м/с), то после их абсолютно упругого столкновения отношение кинетической энергии второго тела к кинетической энергии первого равно 1) 0,34 2) 4,12 3) 3,58 4) 6,86 5) 1,46
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Работа постоянной силы
3.1
Найти работу Аt силы тяжести тела массой m = 1 кг за пятую секунду (t = 5 c) его свободного падения.
3.2
В вертикальную мишень с расстояния S = 100 м сделано два выстрела в горизонтальном направлении при одинаковой наводке винтовки. Найти модуль разности работ А сил тяжести пуль за время их движения до мишени, если масса каждой из них m = 5 г и начальные скорости v1 = 350 м/с и v2 = 320 м/с.
3.3
Тело массой m = 0,3 кг бросают горизонтально с некоторой высоты над землей с начальной скоростью v0 = 15,2 м/с. Найти работу Аmg его силы тяжести между моментом сбрасывания и моментом, когда скорость груза достигает значения v1 = 24,6 м/с.
3.4
Тело массой m = 0,54 кг бросают со скоростью v0 = 26,2 м/с под углом α = 65° к горизонту. Найти работу Аmg его силы тяжести между моментами времени t1 = 0,5 с и t2 = 3 с после начала движения тела.

224 Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ
Работа переменной силы
3.5
Тело массой m = 0,15G кгGв момент времениG t = 0 начинает двигаться под действием силы F = F0 cos ωt , где F0 , ω – постоянные величины ( F0 = 4,5 Н, ω = 0,2 рад/c). Найти работу A(t) этой силы в зависимости от времени и ее работу A(t1 ) до первой остановки тела.
3.6
На движущееся тело массой m в момент времени t = 0 начинает действоватьG зависящая от времени сила сопротивления среды F = F0e−αt , где F0 , α – постоянные величины. Найти работу A(t) этой силы в зависимости от времени и ее работу A0 до остановки тела.
3.7
Тело массой m начинают поднимать с поверхности земли, прикладываяG к немуG зависящую от координаты y вертикальную силу F = 2(ay − 1)mg . Найти работу A( y) этой силы в зависимости от координаты и ее работу A0 до остановки тела.
3.8
Пружина состоит из двух последовательно соединенных пружин с коэффициентами жесткости k1 = 84 Н/м и k2 = 112 Н/м. Найти минимальную работу А, которую необходимо совершить внешней силой, чтобы растянуть пружину на L = 5 см.
Мощность
3.9
Найти среднюю мощность 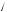 Pmg
Pmg 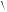 силы тяжести тела массой m = 180 г, брошенного вертикально вверх с начальной скоростью v0 = 22 м/с, при его движении вниз от верхней точки траектории до падения в точку броска.
силы тяжести тела массой m = 180 г, брошенного вертикально вверх с начальной скоростью v0 = 22 м/с, при его движении вниз от верхней точки траектории до падения в точку броска.
3.10
Неподвижное тело массой m = 1,2 кг начинает движение под действием силы F = 30 Н, составляющей угол α = 45° с направлением перемещения. Найти мгновенную мощность P (t ) силы в момент времени t = 16 с и среднюю мощность  P
P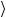 за это время.
за это время.
3.11
Ввертикальную мишень с расстояния S = 400 м сделан выстрел
вгоризонтальном направлении. Найти мгновенную мощность P (t )

Задачи для контрольных работ |
225 |
силы тяжести в момент попадания в мишень и среднюю мощность
 P
P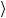 за время движения пули, если ее масса m = 5 г и начальная скорость v0 = 800 м/с.
за время движения пули, если ее масса m = 5 г и начальная скорость v0 = 800 м/с.
3.12
Тело массой m = 450 г брошено со скоростью v0 =16,8 м/с горизонтально поверхности земли с высоты h = 24 м. Найти мгновенную мощность P (t ) его силы тяжести в момент падения на землю и среднюю мощность  P
P за время движения тела.
за время движения тела.
Кинетическая энергия
3.13
С противоположных сторон бесконечно тонкого, невесомого обода, который катится без скольжения по горизонтальной плоскости со скоростью v = 10 м/с, расположены два точечных тела с массами m = 1 г каждый. Найти их кинетические энергии K1 и K2 в момент, когда соединяющий их диаметр образует с вертикалью угол α = 60°.
3.14
Самолет массой m = 12 · 103 кг движется в горизонтальной плоскости по окружности радиусом R = 850 м, имея центростремительное ускорение an = 7,2 м/с2. Найти его кинетическую энергию K.
3.15
Тело массой m = 200 г совершает гармонические колебания x(t) = Asin(ωt + ϕ0 ) на невесомой пружине c амплитудой А = 0,45 м, циклической частотой ω = 18,5 рад/с и начальной фазой ϕ0 = π / 3 рад. Найти зависимость кинетической K (t ) энергии тела от времени t и значение K (t0) кинетической энергии в момент времени t0 = 2 с.
3.16
Тело совершает на невесомой идеальной пружине гармонические колебания x(t) = Asin(ωt + ϕ0 ) . Доказать, что для произвольного мо-
мента времени выполняется соотношение
K (t) + a2 (t) = Km am2 1 ,
где K (t), a(t) — кинетическая энергия и ускорение тела в момент времени t; Km , am — их максимальные значения.
226 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
Теорема об изменении кинетической энергии
3.17
Найти тормозной путь S1 автомобиля, двигающегося на горизонтальном участке со скоростью v1 = 72 км/ч, если при скорости движения v2 = 36 км/ч на этом же участке его тормозной путь S2 = 6,8 м.
3.18
Самолет массой m = 6,2 т, летящий со скоростью v = 720 км/ч, поднимается на h = 2 км. Найти работу А его двигателя при подъеме, если скорость самолета при этом уменьшается v = 120 км/ч.
3.19
Тело массой m = 120 г равномерно вращается по окружности радиусом R = 80 см с частотой ν1 = 5 Гц в горизонтальной плоскости. Какую работу А необходимо совершить для увеличения частоты вращения тела до значения ν2 = 8 Гц без изменения траектории движения?
3.20
Тело массой m = 0,35 кг бросают со скоростью v0 = 28,3 м/с под углом к горизонту. Найти работу Аmg его силы тяжести между броском и моментом времени, когда скорость тела достигает значения v1 = 13,1 м/с. На какой высоте h находится тело при этой скорости?
3.21
Найти импульс тела массой m, движущегося по горизонтальной плоскости без трения, под действием постоянной горизонтальной силы F = 8 Н через t = 15 с после начала движения.
3.22
Тело массой m = 200 г равномерно вращается в горизонтальной плоскости по окружности радиусом R = 95 см с частотой ν = 6 Гц. Какую работу А необходимо совершить для увеличения импульса тела на величину р = 2,2 кг·м/с без изменения траектории движения?
Потенциальная энергия
3.23
Тело массой m = 0,4 кг бросают со скоростью v0 = 24,3 м/с под углом к горизонту. Найти потенциальную U энергию тела в момент времени, когда скорость тела достигает значения v1 = 16,2 м/с.
3.24
Тело массой m = 0,83 кг бросают вверх с некоторой высотыпод углом α = 50° к горизонту с начальной скоростью v0 = 24,5 м/с. Опре-
Задачи для контрольных работ |
227 |
делить потенциальную U энергию тела в точке броска относительно поверхности земли, если в момент падения на землю его скорость в n = 2 раза превышает скорость в высшей точке траектории.
3.25
Тело массой m = 1,2 кг бросают вверх под углом α = 30° к горизонту с высоты h = 18 м с начальной скоростью v0 = 18 м/с. Определить относительно поверхности земли зависимости потенциальной энергии тела U (t) и U (х) от времени t движения и от координаты х. Используя эти функции, найти численные значения времени t0 движения тела до момента падения и координату x0 этой точки.
3.26
Тело массой m = 0,92 кг бросают c поверхности земли под углом к горизонту. Время его движения от броска до момента падения t0 = 5 с и пройденный от начала движения до момента падения путь по горизонтали S = 86 м. Определить относительно поверхности земли зависимости потенциальной энергии тела U (t) и U (х) от времени t движения и от координаты х, если начало координат совпадает с точкой броска и ось Ох проходит через точку падения. Используя эти функции найти численное значение потенциальной энергии в высшей точке траектории тела.
3.27
Тело совершает на невесомой пружине с коэффициентом жесткости k = 214 Н/м гармонические колебания x(t) = Asin(ωt + ϕ0 ) c цик-
лической частотой ω = 14,6 рад/с и начальной фазой ϕ0 = π / 3 рад. Найти его ускорение а0 в некоторый момент времени, когда значение потенциальной энергии пружины достигает значения U0 = 18,2 Дж.
Законы сохранения и изменения энергии
3.28
Доказать, что для тела, брошенного вертикально вверх, на некоторой высоте выполняются соотношения
K = ε |
1 |
; |
U = ε |
n2 − 1 |
, |
||
n2 |
n2 |
|
|||||
|
|
|
|
||||
где n — отношение начальной скорости тела к его скорости на этой высоте; K, U — кинетическая и потенциальная энергии тела на этой же высоте; ε — полная механическая энергия.
228 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
3.29
Тело бросают вертикально вверх с начальной скоростью v0 = 12 м/с. Используя закон сохранения механической энергии, найти высоту h, на которой его скорость в n = 4 раза меньше начальной.
3.30
Через неподвижный блок перекинута нить с двумя грузами на концах, массы которых m1 = 0,5 кг и m2 = 2 кг. Система приходит в движение. Определить скорость v тел, когда каждое из них сместится от первоначального положения на расстояние h = 45 cм. Трением в блоке, массой нити и ее растяжением пренебречь.
3.31
Через неподвижный блок перекинута нить с двумя грузами на концах, массы которых m1 = 0,6 кг и m2 = 2,2 кг. Система приходит в движение и, когда каждое из тел сместится от первоначального положения на расстояние h = 50 cм, их скорость достигает значения v = 2 м/с. Найти силу трения Fтр нити о блок. Массой нити и ее растяжением пренебречь.
3.32
Система, состоящая из неподвижного блока с перекинутой через него нитью с двумя грузами на концах, приходит в движение. Найти силу трения Fтр нити о блок, если к моменту времени, когда каждое из тел смещается на h = 85 cм от своего первоначального положения, их кинетические энергии достигают значений: К1 = 3,82 Дж, К2 = 5,64 Дж и изменения потенциальных энергий тел определяются величинами: U1 = 8,82 Дж, U2 = –19,6 Дж. Массой нити и ее растяжением пренебречь.
3.33
Тело находится у основания плоскости, наклоненной под углом α = 45° к горизонту и обладает скоростью v0, направленной вдоль нее. Найти эту скорость, время t1 движения до остановки, если коэффициент трения тела о плоскость μ = 0,1 и при движении вверх оно останавливается на высоте h = 1 м.
3.34
Тело, движущееся под действием силы трения по горизонтальной плоскости, имеет скорость v0 = 5 м/с, находясь на расстоянии S1 = 4 м от основания плоскости, расположенной под углом α = 60° к горизонту. Максимальная высота, достигаемая телом в момент ос-
Задачи для контрольных работ |
229 |
тановки при движении по этой плоскости, h = 0,41 м. Найти ускорения a1 и a2 тела при его движении на различных участках пути, считая коэффициент трения μ постоянным.
3.35
Тело находится у основания плоскости, наклоненной под некоторым углом α к горизонту, и обладает скоростью v0 = 5м/с, направленной вверх вдоль нее. На высоте h = 1 м от основания скорость тела v1 = 1,85 м/с. Найти коэффициент трения μ тела о плоскость и угол α наклона ее к горизонту, если модуль ускорения тела а = 7,62 м/с2.
3.36
Тело свободно падает с высоты H = 4 м и погружается в сухой песок на глубину h = 18 см. С какой высоты Hx падает груз на влажный песок, если он погружается в него на глубину h1 = 12 см, а средняя сила сопротивления влажного песка возрастает в n = 1,8 раз по сравнению с сухим?
3.37
К свободному концу нити длиной R = 1 м, выдерживающей максимальную силу натяжения Fmax = 20 Н, подвешивается груз массой m = 1 кг, который выводится из положения равновесия и совершает свободные колебания в вертикальной плоскости. Найти максимальную скорость vx прохождения грузом положения равновесия, при которой нить еще не обрывается.
3.38
Тело массой m = 0,53 кг начинает скользить по плоскости, расположенной под углом α = 65° к горизонту. Коэффициент трения тела о плоскость зависит от пройденного пути х по закону μ = k x (k = 0,13). Найти расстояние S, пройденное телом до остановки, и работу А силы трения при его движении.
Импульс
3.39
Тело массой m = 1 кг, двигаясь равномерно, описывает четверть окружности радиуса R = 1,2 м за t = 2 с. Вычислить модуль изменения р импульса тела за это время.

230 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
3.40
Тело движется по криволинейной траектории с тангенциальным ускорением aτ = 0,5 м/с2. Найти его импульс р через t = 3 с после начала движения, если работа действующей на тело силы за это время А = 0,45 Дж.
3.41
Тело массой m = 0,18 кг, брошенное горизонтально c некоторой высоты, через t = 5 с после начала движения имеет импульс p = 10 кг·м/с. Найти импульс p0 тела в момент броска.
3.42
Тело массой m = 0,25 кг брошено горизонтально c некоторой высоты. Найти момент времени t, когда кинетическая энергия достигает значения К = 218 Дж, если в момент броска импульс тела p0 = 5 кг·м/с.
3.43
С противоположных сторон бесконечно тонкого невесомого обода, который катится без скольжения по горизонтальной плоскости со скоростью v = 8 м/с, расположены два точечных тела с одинаковыми массами m = 0,5 г. Найти импульс р1 и р2 каждого из них и их суммарный импульс р в момент, когда соединяющий их диаметр образует с вертикалью угол α = 38°.
3.44
Тело массой m = 0,25 кг совершает гармонические колебания x(t) = Asin(ωt + ϕ0 ) на невесомой пружине c амплитудой А = 0,3 м, цик-
лической частотой ω= 8 рад/с и начальной фазой ϕ0 = π / 12 рад. Найти зависимость модуля импульса тела р (t ) от времени t, его значение р (t0) в момент времени t0 = 2,5 с и максимальное значение рm импульса.
3.45
Тело массой m = 0,12 кг совершает на невесомой идеальной пружине гармонические колебания x(t) = Asin ωt c циклической частотой ω = 16,3 рад/с и амплитудой А = 0,35 м. Для момента времени t = 2,5 c рассчитать значения импульса тела р (t ), его ускорения a (t ), их максимальные значения pm , am и показать выполнение соотношения
p2 (t) + a2 (t) = pm2 am2 1
для полученных значений параметров.
