Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Физика. Механика

.pdf

Скачиваний:

1027

Добавлен:

17.05.2015

Размер:

4.42 Mб

Скачать

☆

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 4426 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>

4.4. Момент импульса системы частиц...

251

На примере простейшей системы частиц (рис.4.6) найдем ее уравнение моментов. Для каждой частицы системы, исходя из уравне-

ний (4.10)
	dLG G
		= M ,
	dt

относительно неподвижной точки О имеем
		dLG	=		G	G
		1			M12внут + M1внеш ,
		dtG			M12внут + M1внеш ,
		dtG			G	G
		dL		=	G	G
	2				M	21внут + M2внеш .
		dt			M	21внут + M2внеш .
		dt

Определим производную по времени момента импульса системы

частиц. С учетом (4.20) и (4.19) получим

G G

d(L1 + L2 )

dL1

dL2

M12внут

+ M1внеш + M

21внут + M2внеш =

dtG

= M1внеш + M2внеш .

Обобщим этот результат на систему, состоящую из произвольно-

го числа частиц.
	dLG	G	внеш	G	внеш
		= ∑ Mi		= M		,	(4.23)
	dt	= ∑ Mi		= M		,	(4.23)
	dt	i

т. е. производная по времени момента импульса системы частицы относительно неподвижной точки О равна векторной сумме моментов внешних сил, приложенных к частицам системы (сравните с выражением (4.10) для одной частицы). Уравнения (4.23) называются уравнением моментов системы частиц. Из (4.23) следует закон сохранения момен-

та импульса системы частиц:			G
G			G	(4.24)
если M внеш = 0 , то			L = const,	(4.24)
или
LG(t ) = LG	(t	2	) .
1		2

Если векторная сумма моментов внешних сил, действующих на частицы системы относительно неподвижной точки, равна нулю, то момент импульса системы частиц остается постоянным (сравните с (4.11)). Если система изолирована (замкнута), т. е. на частицы системы не действуют внешние силы, то суммарный момент этих сил равен нулю и, следовательно, момент импульса изолированной системы частиц остается постоянным.

252	Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Отметим, что во всех случаях, когда момент импульса системы частиц постоянен, моменты импульса отдельных частиц, составляющих систему, могут меняться со временем. Проектируя на ось z векторные уравнения (4.20,4.23) получим

Lz	= ∑ Liz ,	(4.25)
dLz	i
dLz	= M zвнеш .	(4.26)
dt	= M zвнеш .	(4.26)
dt

Здесь Lz – момент импульса системы частиц относительно неподвижной оси, а M zвнеш – сумма моментов внешних сил, действующих на систему частиц относительно неподвижной оси. Уравнение (4.26) называется уравнением моментов системы частиц относительно неподвижной оси. Из (4.26) следует закон сохранения проекции момента импульса системы частиц (сравните с (4.17)):

если M внеш = 0 , то	L = const,	(4.27)
z	z

или

Lz (t1 ) = Lz (t2 ) .

Если алгебраическая сумма моментов внешних сил, действующих на все частицы системы относительно некоторой неподвижной оси равна нулю, то момент импульса системы частиц относительно этой оси остается постоянным.

Вопросы и задания для самопроверки

1.Докажите, что сумма всех внутренних сил системы частиц равна нулю.

2.Докажите, что сумма моментов внутренних сил равна нулю.

3.Запишите уравнение моментов импульса системы частиц.

4.Запишите уравнение моментов импульса системы частиц относительно оси.

5.Сформулируйте закон сохранения момента импульса системы частиц.

6.Как меняется со временем момент импульса замкнутой системы частиц?

7.Могут ли меняться со временем моменты импульса частиц, составляющих замкнутую систему?

= FGвнеш .

4.5. Центр масс системы частиц						253
4.5. ЦЕНТР МАСС СИСТЕМЫ ЧАСТИЦ
Центром инерции или центром масс систе-
мы частиц называется точка С, радиус-вектор						С
которой rG определяется формулой						С
C
rGC = 1	∑mi rGi	,	(4.28)		G	m i
m	i			y	G	m i
где				y	rC	Gri
где				O		Gri
m = ∑mi			(4.29)	O	x
m = ∑mi		G	(4.29)	z	x
	i	G	– радиус-век-
— масса системы частиц, а		ri	– радиус-век-

тор i частицы (рис. 4.7).

Декартовы координаты точки центра масс (или проекции радиус-
вектора rG	) в некоторой инерциальной системе отсчета имеют вид
C		1			1			1
	xC =		∑mi xi ,	yC =		∑mi yi ,	zC =		∑mi zi .	(4.30)
		m			m			m
			i			i			i

Если число частиц системы и их масса не меняются со временем,

то скорость точки центра масс vG

определяется как

drGi

vGC =

drC

(

∑mi rGi ) =

∑mi

∑mi vGi

∑ pGi

pG ,(4.31)

dt m

где pG = ∑ pGi — импульс системы частиц. Следовательно, можно за-

писать

pG = mvG ,

(4.32)

т. е. импульс произвольной системы частиц в любой инерциальной систе-

ме отсчета равен произведению массы системы на вектор скорости ее

центра масс. Определим ускорение центра масс системы как

dvGC

(4.33)

Продифференцируем импульс системы pG (4.32) по времени с уче-

том определений vG

(4.31) и aG

(4.33)

dmvGC

dvGC

d 2 rGC

dpG

= m

= ma .

dt2

ПриG рассмотрении закона сохранения импульса показано, что если p – импульс системы частиц, то

dpG = ∑ FGвнеш dt i i

254	Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Тогда получаем уравнение движения центра масс

maGC = m d 2 rGC = FGвнеш . (4.34) dt2

Из этого уравнения видно, что центр масс произвольной системы движется так, как двигалась бы частица, масса которой равна сумме масс частиц системы, на которую действует сила, равная сумме внешних сил, приложенных к частицам системы. Отметим, что совершенно не важно, к каким частицам системы приложены внешние силы. Таким образом, движение центра масс описывает движение произвольной системы частиц в целом. Рассмотрим несколько примеров движения центра масс различных систем.

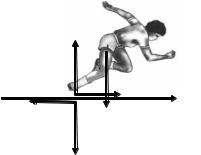
Прыжок кошки

Если кошка прыгает горизонтально (рис. 4.8), то ее центр масс перемещается так же, как перемещается камень (материальная точка) равной массы, брошенный горизонтально с той же высоты и с той же начальной скоростью. На кошку и камень в полете действует одна и та же внешняя сила тяжести (трением о воздух пренебре-

гаем). Поэтому	G	G		G
	G	G	внеш	G
	ma	= F		= mg .
	C

За счет внутренних сил кошка может только менять положение частей своего тела (кувыркаться), но не может изменить положение своего центра масс. Так же как и камень, центр масс кошки движется в поле тяжести земли по параболе.

парабола

G G

P mg

Рис. 4.8

4.5. Центр масс системы частиц

255

Движение человека

При отсутствии сил трения человек (рис. 4.9) не мог бы двигаться в горизонтальной плоскости, так как в этом случае сумма проекций всех приложенных к человеку внешних сил (тяжести и нормальной составляющей реакции опоры) на любую горизонтальную ось равна нулю. Следовательно,

maCx = Fxвнеш = Nx + Px = 0 .

		G
		FТр	x
G	G	G	x
G	G	G
`	P mg
FТр

Рис. 4.9

За счет внутренних сил человек, как и кошка, может только изменить положение частей своего

тела (ног, рук), но не положение своего центра масс. При ходьбе или беге человек выносит одну ногу вперед, приподнимая ее над землей, чтобы исключить действие на нее силы трения. Другая нога движется назад. Ей препятствут сила трения, приложенная к человеку и направленная вперед по его движению. Эта сила и есть та внешняя сила, которая позволяет центру масс человека перемещаться в нужном направлении.

Движение человека на лыжах, автомобиля по дороге, поезда по рельсам

Если человек движется на лыжах, то против движения ноги вперед действует сила трения, направленная назад, а против движения ноги назад — сила трения, направленная вперед. Из-за наличия специальной мази сила трения, направленная назад, меньше по величине силы трения, направленной вперед. Векторная сумма сил трения является той результирующей внешней силой, которая перемещает центр масс человека вперед и, следовательно, позволяет ему двигаться на лыжах в нужном направлении. Наличие лыжных палок добавляет к силам трения, приложенным к лыжам, внешнюю силу сопротивления, приложенную к палкам и направленную по направлению движения лыжника. Движение автомобиля и поезда также связано с тем, что силы трения, приложенные к колесам и направленные по

256	Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

движению, больше по величине сил трения, направленных против движения.

Вопросы и задания для самопроверки

1.Дайте определение радиус-вектора и его координат, скорости и ускорения центра масс механической системы в произвольной инерциальной системе отсчета.

2.Дайте определение импульса системы частиц через скорость ее центра масс.

3.Объясните, почему барон Мюнхгаузен не мог вытащить сам себя за волосы из болота.

4.Объясните динамику ходьбы и бега человека, движения автомашины.

Примеры решения задач

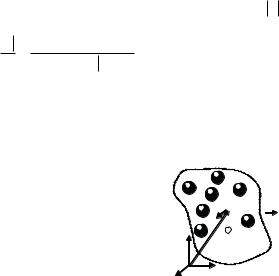
Задача 4.5

Gr1`

Найти центр масс (т. С ) сис-

Gr1

темы двух частиц с радиус-векто-

GrC

рами rG1 и rG2 и массами m1 и m2

Gr2

Дано: m1; m2; rG1 ; rG2 .

Найти: положение т. С.

Пусть т. С — неизвестный центр масс системы двух частиц. По

правилу сложения векторов получаем

rG′ = rG

− rG

rG′ = rG − rG .

(1)

Подставим в (1) выражение для rG

(4.28)

−

m1rG1

+ m2 rG2

m1rG1 + m2 rG1 - m1rG1

− m2 rG2

r′ = r

+ m2

m1 + m2

(2)

m2 rG1 − m2 rG2

− r )

m1 + m2

−

m1rG1

+ m2 rG2

m1rG2 + m2 rG2 - m1rG1

− m2 rG2

r′ = r

+ m2

m1 + m2

(3)

m1rG2 − m1rG1

− r ).

m1 + m2

4.6. Ц-система

257

Так как

(rG

− rG ) ↑↓

(rG

− rG) ,

то

rG′ ↑↓

rG′ .

Следовательно, эти вектора лежат на одной прямой. Пусть l1 =

и l

rG′

. Тогда

rG′

− rG

(m + m )

1G G2

r′

(m + m )m r

− r

rG1′

(4)

Ответ: центр масс системы двух частиц с массами m1 и m2 расположен на прямой, соединяющей эти частицы, и делит ее на части в соотношении m2 к m1, считая от частицы с массой m1.

4.6. Ц-СИСТЕМА

Для упрощения расчетов удобно рассматри-
вать движение системы частиц относительно
ее центра масс. Систему отсчета, жестко свя-
занную с центром масс и перемещающуюся по-
ступательно (т. е. без вращения) по отношению		y
к инерциальным системам отсчета, называют		O
системой центра масс или кратко Ц-системой.		O
системой центра масс или кратко Ц-системой.		z
(рис. 4.10). Из выражения (4.34)	Gвнеш
G	Gвнеш
ma	= F
C

С vGC

GrC

Рис. 4.10

следует:

если сумма внешнихG сил, приложенных ко всем частицам системы, равна нулю, то aC = 0 и центр масс системы будет двигаться равномерно и прямолинейно или оставаться в покое относительно инерциальной системы отсчета, т. е. Ц-система будет инерциальной системой;

если сумма внешнихG сил, приложенных ко всем частицам системы, не равна нулю, то aC ≠ 0 и центр масс будет двигаться с ускорением относительно инерциальной системы отсчета, т. е. Ц-система будет неинерциальной системой. Так как система координат в Ц-сис- теме жестко связана с центром масс, то, очевидно,

rG	≡ 0 ,	vG	≡ 0 и aG	≡ 0 .	(4.35)
СЦ		СЦ	СЦ

258 Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Следовательно, суммарный импульс системы частиц в Ц-систе-

ме (4.32)	= mvG
pG	= mvG	≡ 0.	(4.36)
Ц	СЦ

Уравнения моментов системы и уравнение моментов системы относительно оси (4.23, 4.26) в соответствии с принципом относительности Галилея инвариантны относительно преобразования Галилея, т. е. имеют одинаковый вид в любой инерциальной системе отсчета. Рассматривая моменты импульса и сил системы частиц относительно движущегося начала (точки) и движущейся оси, можно показать, что уравнения моментов и их проекций на ось остаются инвариантными (неизменными) и при переходе из инерциальной системы отсчета в Ц-систему, которая может быть как инерциальной, так и не-

инерциальной. Таким образом,Gимеют место равенства
			dL	G
			Ц	= MЦвнеш ,	(4.37)
			dt	= MЦвнеш ,	(4.37)
			dt
		dLЦz		= MЦвнешz ,	(4.38)
G			dt	= MЦвнешz ,	(4.38)
			dt
	G
где L	, M внеш – момент импульса системы частиц и сумма моментов
Ц	Ц

внешних сил, рассчитанных относительно центра масс системы, который в общем случае не является неподвижным.

4.7. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО. РАВНОДЕЙСТВУЮЩАЯ СИЛ, ПРИЛОЖЕННЫХ К ТВЕРДОМУ ТЕЛУ.

РАВНОДЕЙСТВУЮЩАЯ СИЛ ТЯЖЕСТИ

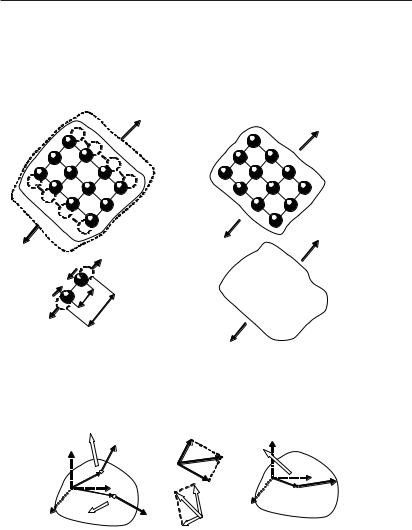
Рассмотрим частный случай — систему частиц с абсолютно жесткими связями. Модель такой системы — абсолютно твердое тело

(рис. 4.11). Следствием абсолютной твердости (жесткости) связей является неизменность расстояний между любыми двумя частицами и размеров всего тела при произвольном воздействии на систему (т. е. отсутствие деформаций, а значит и внутренних сил). Следовательно,

абсолютно твердое тело — модель макроскопического тела, размерами которого в рамках данной задачи нельзя пренебречь, но можно пренебречь изменениями этих размеров, т. е. деформациями.

При замене дискретной системы частиц на непрерывную неизменным остается расстояние между любыми двумя точками абсолютно

4.7. Абсолютно твердое тело. Равнодействующая сил...

259

твердого тела. Далее вместо термина абсолютно твердое тело используется термин твердое тело. Если система частиц представляет собой одно твердое тело, то индекс «внеш» ни у сил, ни у их моментов указываться не будет, так как для одного твердого тела все силы внешние.

			G				Твердое тело
			G	внеш
			F1						FG1
									FG1
									Дискретная
									система
						FG2			a 0
	F1	G	G			FG2			G
	F1	G	G						F1
	G внеш
	fG21	f12	f1						Непрерывная
									Непрерывная
		a1							система
	G	a1	a2			FG2
	f 2					FG2			a 0
	a a2	a1 – деформация							a 0
	a a2	a1 – деформация
						Рис. 4.11
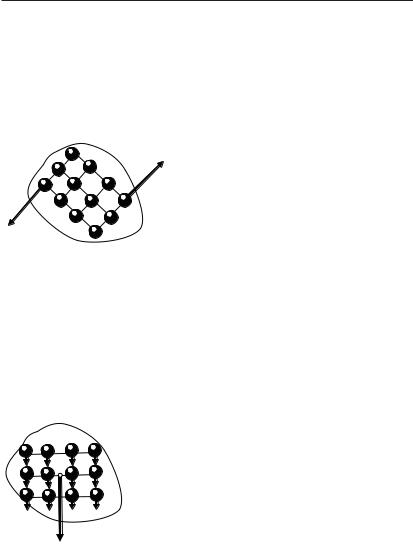
G	Назовем равнодействующей сил, приложенных к твердому телу, силу
F	равн (рис. 4.12):
		G	FG2		G
		M 2	FG2		F2	FGравн	G	равн
		Gr2		G		G	M		Gравн
		Gr2					G		Gравн
					равн		G		F
		Gr1	G	M		F1	r
		Gr1	G	G		G
			M1	F1	G	M 2
					M1
						Рис. 4.12
равную сумме сил, действующих на твердое тело
					FGравн = ∑FGi ,				(4.39)

i=1

260 Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

момент которой относительно произвольной точки О равен сумме моментов всех сил относительно этой точки

		G равн	G G	равн		G	G	G
		M	=[r, F		] = ∑[r , F ] = ∑M				i .	(4.40)
						i	i		i .	(4.40)
Здесь rG						i=1		i=1
Здесь rG	— радиус-вектор i частицы (точки) тела, к которой прило-
i		относительно точки О, rG – неизвестный радиус-вектор
жена сила FG		относительно точки О, rG – неизвестный радиус-вектор
	i					точки приложения равнодействую-
						точки приложения равнодействую-
			G		G	щей силы относительно точки О.
			F1	F		В общем случае совокупность
						сил, приложенных к твердому телу,
						может не иметь равнодействующей
FG2 FG						силы. Это значит, что не существует
FG2 FG						одной силы, которой можно заме-
	Рис. 4.13					нить действие всех приложенных
						сил. Простейшим примером явля-

ется действие на твердое тело пары сил, т. е. одинаковых по модулю, но противоположных по направлению сил, приложенных к разным частицам (точкам) тела. (рис.G 4.13)G .GИх сумма

F = F1 + F2 = 0 .

Результатом воздействия на тело пары сил является его вращение. Очевидно, что действие нулевой силы, т. е. отсутствие какоголибо воздействия на систему, не эквивалентно действию двух указанных выше сил.

mi gG

FG mgG

Рис. 4.14

Отметим, что для сил, приложенных к одной частице (4.8), равнодействующая сила существует всегда.

Рассчитаем равнодействующую параллельных сил. Например сил тяжести твердого тела, представляющего собой дискретную систему частиц с абсолютно жесткими связями. Найдем модуль, направление и точку приложения равнодействующей (рис. 4.14). По определению (4.39–4.40)

FGравн = ∑FGi = ∑mi gG = mgG ,

i=1

<<< < Предыдущая 14 15 16 17 18 19 20 21 22 23 24 2526 / 4426 27 28 29 30 31 32 33 34 35 36 37 38 > Следующая >>>