
Набор учебников PDF Хороший солдат / Физика / Физика. Механика
.pdf3.2. Работа силы. Мощность |
161 |
и вертикальную оси |
|
mg − T cos α = 0 . |
(3) |
Из последнего соотношения получим модуль силы натяжения
нити |
|
|
|
T = |
mg |
. |
(4) |
|
|||
|
cos α |
|
|
Подставляя (4) в равенство (2), получим зависимость модуля внеш-
ней силы от угла α |
|
F = mgtgα . |
(5) |
(Обратите внимание, что внешняя сила — переменная величина, зависящая от угла α.). Учитывая, что внешняя сила параллельна оси
ОХ, представим ее в виде |
|
|
G |
G |
|
F |
= imgtgα; (Fx = mgtgα; Fy = 0) . |
(6) |
Входящее в формулу для элементарной работы |
|
|
|
dAF = (FG, dSG) = Fx dSx + Fy dSy |
(7) |
элементарное смещение dSG , можно представить следующим обра-
зом (рис. 2) |
G |
G |
G |
G |
G |
|
|
(8) |
|||||
|
dS |
= idx + |
jdy = i cos αdS + j sin αdS . |
|||
Найдем проекции смещения dSG |
на оси координат (рис.2) |
|
||||
|
|
dx = cosαdS; |
|
dy = sinαdS . |
(9) |
|
Подставляя в формулу (7) проекции внешней силы (6) и смещения (9), получим
dAF = mg tgα cosαdS G= mg sinαdS = mg dy. |
|
Следовательно, работа силы F имеет вид |
|
α0 |
y0 |
AF = ∫ mg sin αdS = mg ∫ dy = mgy0 , |
|
0 |
0 |
где y0 = L(1 – cosα0) — координата материальной точки при отклонении нити маятника на угол α0 (рис. 1). В последнем соотношении учтено, что dy = sin αdS . Окончательный результат имеет вид
AF = mgL(1 – cosα0).

162 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
2. Сила натяжения нити TG |
не совершает работы, так как она дей- |
ствует в направлении, перпендикулярном перемещению материальной точки
dA |
= (TG, dSG) = TdS cos π = 0 → AT = 0. |
||||
T |
|
|
|
2 |
|
3. Работа силы тяжести определяется соотношением |
|||||
|
|
Amg |
α0 |
G G |
|
|
|
= ∫ mgdS . |
(10) |
||
|
|
|
0 |
|
|
Принимая во внимание, что |
G |
G G |
|||
mgG |
G |
G |
G |
||
= − jmg, |
dS |
= idx + jdy , (i , j) = 0 , |
|||
перепишем (10) в виде
y0
Amg = − ∫ mgdy = −mgL(1− cos α0 ) .
0
Отметим, что полная работа, совершаемая всеми силами, действующими на материальную точку, равна нулю
AF + AT + Amg = 0,
что согласуется с тем, что результирующая сила, действующая на материальную точку, согласно условию задачи (1), равна нулю.
Примечание: сравните решение этой задачи с решением задачи 3.3. Ответ: AF = mgL(1 – cosα0); AT = 0; Amg = –mgL(1 – cosα0).
3.3. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Энергия — одно из наиболее значительных понятий в физике. Будем рассматривать энергию как «способность тела совершать работу»1.
Такой подход не вполне точен и не применим ко всем видам энергии, вводимым в различных разделах физики. Однако его достаточно для механической энергии, обсуждаемой в настоящей главе. Определим теперь один из основных видов энергии — кинетическую энергию.
1 Строго говоря, работу совершает не тело, а возникающая при контакте тел сила. Такая «подмена» определения работы силы не приводит к искажению существа вопроса. Действительно, в данном случае причиной появления сил является контактное взаимодействие тел, которые являются носителями сил, совершающими работу.

3.3. Кинетическая энергия |
163 |
Движущееся тело может совершить работу над другим телом при контактном взаимодействии с ним. Действительно, летящее пушечное ядро совершает работу, проламывая стену. Падающий на гвоздь молоток совершает работу по его забиванию. В обоих случаях движущееся тело действует с определенной силой на второе тело и перемещает его на некоторое расстояние. Таким образом, при контактном взаимодействии двух тел, движущегося и неподвижного, возникает сила и перемещение, т. е. совершается работа. Поскольку движущееся тело способно совершить работу, то оно обладает энергией. Энергия механического движения называется кинетической энергией.
Для того чтобы получить количественное определение кинетической энергии, рассмотрим частный случай одномерного движения. Пусть на неподвижное тело, находящееся наGгоризонтальной плоскости, вдоль нее действуетGпостоянная сила F . Тогда система уравнений, связывающая силу F , скорость v (t) тела, пройденный путь S за время t и работу А, совершаемую силой, имеет вид
F = ma; |
|
v |
|
(3.12) |
|||
v = at → t = |
; |
(3.13) |
|||||
a |
|||||||
|
at2 |
|
|
|
|||
S = |
; |
|
|
(3.14) |
|||
2 |
|
|
|
||||
|
|
|
|
|
|
||
A = FS. |
|
|
|
(3.15) |
|||
Подставляя в соотношение (3.15) соответствующие параметры (3.12-3.14), получим выражение для работы
A = FS = ma at2 = 1 ma2
2 2
принимающее окончательный вид
A = FS = mv2 2 .
v |
2 |
||
|
|
|
, |
|
|||
a |
|
||
(3.16)
Теперь выясним, какую работу могут совершить силы, возникающие при столкновении двух тел. Пусть движущееся тело имеет скорость v, другое тело неподвижно. Для простоты полагаем, что со стороны неподвижного на движущееся тело, действует постоянная сила

164 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
FG′ (сила FG′ приложена к движущемуся телу). Система уравнений в скалярной форме аналогичная (3.12–3.15), имеет вид
F ′ = ma ′;
v – a ′t ′ = 0 →
S ′ = vt′ − a′t′2
2
A = FS cos π.
t′ = av′ ;
;
(3.17)
(3.18)
(3.19)
(3.20)
Здесь t ′– время, в течение которого движущееся тело останавлиG - вается; S ′ — путь, пройденный точкой приложения силы; a′ – ускорение этой точки (для простоты считается постоянным), сила F ′ совершает отрицательную работу A ′, так как направления силы и перемещения противоположны. Теперь в соотношение (3.20) подставим (3.17–3.19)
|
a′t′2 |
v2 |
|
a′ v2 |
||||
A′ = − F ′S ′ = −ma′ vt′ − |
|
|
= −ma′ |
|
− |
|
|
. |
|
|
2 a′ |
2 |
|||||
|
2 |
a′ |
|
|
|
|||
После простых преобразований имеем
A′ = − F ′S ′ = − |
mv2 |
. |
(3.21) |
|
2 |
||||
|
|
|
Обратим внимание на то, что со стороны движущегося тела к неподвижному также приложена сила. СогласноG третьему закону Ньютона она по модулю совпадает с силой F ′ , но противоположна ей по знаку. Работа, совершенная этой силой, очевидно, определяется соотношением
так как вектор перемещения движущегося тела и сила (− FG′) направлены в противоположные стороны. Отсюда следует равенство
A ′ + A ′′ = 0.
Из приведенных простых примеров можно сделать очень важные выводы. Когда на покоящеесяG тело начинает действовать постоянная по направлению сила F , то приобретаемая им скорость vG совпадает по направлению с силой и возрастает по величине. При этом сила совершает положительную работу (3.16), так как перемещение тела
3.3. Кинетическая энергия |
165 |
совпадает по направлению с силой. Наоборот, если на движущееся тело начинает действовать сила, направленная навстречу его скорости (со стороны второго тела при столкновении), то скорость тела уменьшается, сила к нему приложенная совершает отрицательную работу (3.21), так как перемещение тела и сила направлены в противоположные стороны. Сила способна совершать работу до тех пор, пока скорость движущегося тела не уменьшится до нуля.
Таким образом, в результате работы внешней силы тело приобретает определенную скорость, а вместе с тем и способность совершать
работу, теряя скорость (3.21). При этом |
|
A + A ′ = 0. |
(3.22) |
Последнее равенство означает, что движущееся тело способно совершить ровно столько работы, сколько оно предварительно «запасает» под действием внешней силы.
Движущееся со скоростью v тело массой m, если его остановить совершает работу по модулю, равную (3.21). Данное выше качественное определение энергии как способности тела совершать работу, совместно с соотношением (3.21), позволяет ввести энергию тела, связанную с его движением, следующим образом
K = |
mv2 |
. |
(3.23) |
|
|||
2 |
|
|
|
Последнее соотношение представляет собой кинетическую энергию движущегося тела.
Рассмотрим более общий, чем приведенныйG выше случай. Пусть на тело действует переменная внешняя сила F , увеличивающая его
скорость, т. е. сила совершает работу над этим телом. Тогда ее работа |
|
на произвольной траектории S определяется соотношением (3.7) |
|
A = ∫(FG, dSG) . |
(3.24) |
S
Если воспользоваться вторым законом Ньютона и определением
мгновенной скорости |
|
dvG G |
|
|
|
G |
|
G |
|
||
F |
= m |
|
; dS |
= vdt , |
|
dt |
|
||||
то (3.24) можно переписать в следующем виде: |
|
||||
A = ∫ m(dvG, vG) = ∫ m(vG, dvG) . |
(3.25) |
||||
S S

166 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
Подынтегральное выражение представим в форме |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
G G |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
(v, dv) = |
|
dv |
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
Действительно, с одной стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
G |
dvG |
|
|
dvx |
|
+ vy |
dvy |
+ vz |
dvz |
|
|
|
|
|||||||||
|
|
|
|
|
|
(v, |
|
) = vx |
|
|
|
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
dt |
dt |
|
dt |
dt |
|
|
||||||||||||||||
С другой стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dvy |
|
|
|||||||
|
1 dv2 |
= v |
dv |
= v |
d |
v2 |
+ v2 |
+ v2 = v |
|
|
dv |
x |
+ v |
|
|
+ v |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 dt |
dt |
dt |
|
|
dt |
|
|
dt |
|
||||||||||||||||||
|
|
|
|
x |
|
y |
|
|
z |
|
x |
|
|
y |
|
|
z |
|||||||||||
(3.26)
(3.27)
dvdtz . (3.28)
Сравнение соотношений (3.27) и (3.28) подтверждает правильность формулы (3.26). С учетом сказанного перепишем (3.25) в виде
A = ∫ |
d mv2 |
= |
mv2 |
. |
|||
|
|
|
|
|
|||
|
|
2 |
|||||
S |
dt |
2 |
|
|
|||
Отсюда следует, что формула (3.21), введенная для кинетической энергии на основании рассмотрения частного примера, не изменяется и в общем случае.
G Если же скорость телаG подG действием приложенной к нему силы F ′ уменьшается, то (F ′, dS ′) < 0. В этом случае говорят, что тело совершает работу. Проведя аналогичные преобразования, получим
A′ = ∫ (FG′, dSG′) = − mv2 . |
|
S |
2 |
Сравнение последнего соотношения с формулой (3.21) подтверждает сделанный ранее вывод о том, что тело не может совершить большую работу, чем его кинетическая энергия.
Теорема об изменении кинетической энергии
Пусть приG движении по траектории S на тело одновременно действуют силыG F , увеличивающие (или не изменяющие) скорость тела, и силыGF ′ ,Gпрепятствующие этому процессу. В общем случае каждая из сил F и F ′ может представлять собой сумму сил, приводящих к возрастанию скорости тела и уменьшающие ее. Например, силы тяги и трения, действующие на автомобиль, (силы тяжести и реакции не совершают работы и не изменяют скорость автомобиля). Согласно опре-
делению, работа всех сил приложенных к телу, представима в виде |
|
A + A′ = ∫ (FG + FG′, dSG) . |
(3.29) |
S
3.3. Кинетическая энергия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
167 |
Принимая во внимание, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||
G |
G |
|
dvG |
G |
|
|
G |
|
|
|
|
|
|||
F |
+ F ′ |
= m |
|
; |
dS |
= vdt , |
|
|
|
|
|||||
dt |
|
|
|
|
|||||||||||
представим (3.29) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G G |
v2 |
d mv2 |
|
mv22 |
|
mv12 |
|
|
||||||
A + A′ = ∫ m(v, dv) = ∫ |
|
|
|
|
|
|
= |
|
− |
|
. |
(3.30) |
|||
|
|
|
|
|
|
||||||||||
S |
|
v |
dt |
2 |
|
|
|
2 |
|
2 |
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В последнемGравенствеG v1 — модуль начальной скорости тела, при которой силы F и F ′ начинают на него действовать; v2 — конечная скорость тела. Если ввести обозначения
|
mv2 |
|
|
mv2 |
|
|
K = |
1 |
; K |
2 |
= |
2 |
(3.31) |
|
|
|||||
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
||
начальной и конечной кинетической энергии тела, то соотношение (3.30) можно записать в форме
A + A ′ = K2 – K1 = K, |
(3.32) |
где K – изменение кинетической энергии тела, произошедшее изза работы приложенных к нему сил. Следовательно, полная работа сил, действующих на тело, равна изменению его кинетической энергии.
Это утверждение носит название теоремы об изменении кинетической энергии. Его иногда называют теоремой о связи работы и кинетической энергии.
Заметим, что теорема об изменении кинетической энергии не является новым независимым законом. Она установлена на основании определений работы и кинетической энергии с использованием второго закона Ньютона.
Вопросы и задания для самопроверки
1.Определите кинетическую энергию как «способность движущегося тела совершать работу» и приведите качественные примеры того, что тело, обладающее скоростью, способно совершать работу.
2.Определите условия, при выполнении которых движущееся тело совершает работу.
3.На простых примерах математически обоснуйте утверждение, что движущееся тело не может совершить работу, превышающую его кинетическую энергию.

168 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
4.Дайте качественную интерпретацию формулы (3.22).
5.Может ли кинетическая энергия быть отрицательной?
6.Сформулируйте и докажите теорему об изменении кинетической энергии.
Примеры решения задач
Задача 3.7
Тело массой m = 100 г на нити длиной L = 40 см, закрепленной с одной стороны, движется в горизонтальной плоскости с постоянной по модулю скоростью. Найти кинетическую K энергию тела, если нить образует с вертикалью угол α = 60°.
Дано: m = 0,1 кг; L = 40 см; α = 60°. Найти: К.
Для решения задачи запишем следующую систему уравнений:
K = |
|
mv2 |
– кинетическая энергия тела; |
(1) |
||||
2 |
||||||||
G |
|
G |
|
|||||
|
|
G |
|
(2) |
||||
mg |
+ T |
= ma — второй закон Ньютона; |
||||||
G |
|
v2 |
G |
|
|
|||
a = |
|
|
n — центростремительное ускорение тела; |
(3) |
||||
|
R |
|||||||
R = L sin α – радиус траектории движения тела. |
(4) |
|||||||
В уравнении (3) системы nG – единичный вектор, совпадающий по направлению с центростремительным ускорением. Запишем уравне-
ние (2) с учетом (3), в виде проекций на горизонтальную |
|
|||
T sin α = |
mv2 |
|
(5) |
|
R |
||||
|
|
|||
и вертикальную оси |
|
|
|
|
T cos α = mg . |
(6) |
|||
Из последнего соотношения получим модуль силы натяжения
нити |
|
|
|
T = |
mg |
. |
(7) |
|
|||
|
cos α |
|
|
3.3. Кинетическая энергия |
169 |
Подставив (7), совместно с радиусом окружности (4), в соотношение (5), имеем
mgL sin αtgα = mv2 .
Если обе части полученного равенства разделить на два, то получим выражение для кинетической энергии (1) тела, вращающегося на нити, и ее численное значение, представленные в ответе.
Ответ: K = mgL2 sin αtgα = 0,294 (Дж).
Задача 3.8
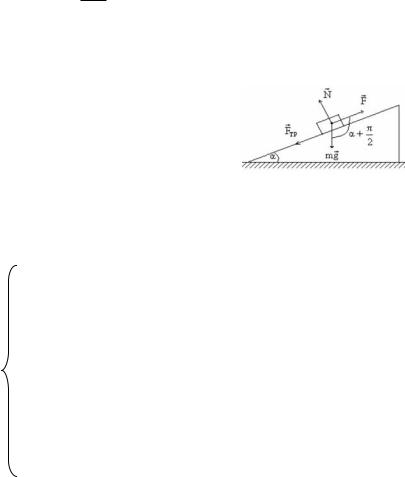
Тело поднимают равномерно вверх по плоскости с углом α ее наклона к горизонту и коэффициентом трения μ. Вычислить коэффициент полезного действия η подъема тела по наклонной плоскости.
Дано: α; μ. Найти: η.
Пусть Aзатр = AF – полная работа, совершенная силой тяги F при равномерном перемещении тела на некоторое расстояние S вдоль наклонной плоскости; Aпол —
полезная работа, часть полной работы силы F без учета работы совершенной этой силой при ее преодолении силы трения. Дополняя соотношение для коэффициента полезного действия ηформулами для работы сил, действующих на тело и используя теорему об изменение кинетической энергии тела, запишем следующую систему уравнений:
|
A |
AF − |
Aтр |
|
|
||
η = |
пол |
= |
|
|
|
— |
|
|
|
|
|
|
|||
|
Aзатр |
AF |
|
||||
определение коэффициента полезного действия; |
(1) |
||||||
Азатр = АF – работа силы тяги; |
(2) |
||||||
Aпол = AF – |Aтр| — |
|
||||||
полезная работа, совершенная силой тяги; |
(3) |
||||||
Атр + AN + AF + Amg = 0 — |
|
||||||
теорема об изменении кинетической энергии; |
(4) |
||||||
Атр = –μmgS cosα — работа силы тренияG(см. рис); |
(5) |
||||||
AN = 0 — работа силы реакции (вектор N перпендикулярен |
|
||||||
перемещению); |
(6) |
||||||
Amg = mgS cos(π/2 + α) = –mgS sinα — |
|
||||||
работа силы тяжести (см. рис). |
(7) |
||||||

170 |
Глава 3. РАБОТА И ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ |
μ– коэффициент трения тела о поверхность; S – путь пройденный телом вдоль поверхности. Правая часть уравнения (4) равна нулю, так как тело движется равномерно и его кинетическая энергия не меняется.
Из соотношения (4), учитывая (6), получим
AF = Aтр – Amg = mg S (μcosα + sinα). |
(8) |
Подставив (8) и (5) в (1), получим коэффициент полезного действия
η = |
mg sin α |
|
|
. |
|
μmg cos α + mg sin α |
||
Окончательный результат имеет вид, представленный в ответе.
Ответ: η = |
1 |
. |
μctgα + 1 |
3.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Консервативные и неконсервативные силы
Вмеханике широко используется понятие силового поля — ограниченная или неограниченная область пространства, в каждой точке которого на тело1 действует сила, в общем случае зависящая от координат и времени. Если работа сил поля, действующих на перемещающееся в нем тело, определяется только начальным и конечным положениями тела в пространстве и не зависит от вида его траектории, то силовое поле называется потенциальным, а силы, приложенные к телу со стороны поля, — консервативными или потенциальными.
Взадаче 3.4 показано, что сила тяжести — консервативная, так как
ееработа не зависит от формы пути и определяется лишь начальными и конечными точками траектории движения тела.
Центральная сила — приложенная к телу сила, линия действия которой при любом положении тела проходит через некоторую оп-
1 Здесь и далее под телом понимается либо материальная точка, либо объект, размеры которого значительно меньше рассматриваемой физической системы или траектории, по которой он движется. Используется для того, чтобы отличать материальную точку от пространственной.
