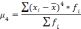13. Средние структурные величины и показатели центра распределения

Средние структурные величины. 1.Мода распределения – чаще всего встречающиеся значения признака, которые соответствуют максимальной точке кривой распределения .

Мода – величина изучаемого признака, которая в данной совокупности встречается наиболее часто. В дискретном ряду распределения моде соответствует варианта с наибольшей частотой. В интервальном ряду распределения с равными интервалами мода рассчитывается по формуле:

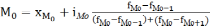
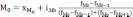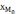
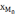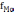
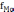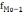
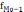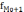
,где - нижняя граница модального интервала; , , 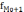- частоты, соответственно, модального интервала, интервала предшествующего модальному, и интервала, последующего за модальным.

2. Медиана – величина, которая делит численность упорядоченного вариационного ряда на две равные части.

Для дискретного ряда распределения – с нечетным числом интервалов медианой является варианта, расположенная в центре ряда; с четным числом интервалов – медиана рассчитывается как средняя арифметическая из двух смежных центральных вариант.

Для интервального ряда распределения медиана находится при помощи накопленной частоты.

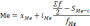где Хме – нижняя граница медианного интервала S.

Показатели центра распределения – основные средние степенные и средние структурные величины ряда распределения рассчитываются по формулам:

• Средняя арифметическая взвешенная величина позволяет учитывать структуру совокупности

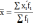
14. Показатели формы распределения

Основные показатели формы распределения – асимметрия и эксцесс – характеризуют степень отклонения реального рассматриваемого распределения от нормального распределения.

Асимметрия– показатель отклонения реального распределения от нормального в правую или левую сторону. Симметричным считается распределение, в котором частоты любых двух вариантов, равно отстоящих в обе стороны от центра распределения, равны между собой. Симметричные распределения характеризуются соотношением: =МеМо.Значение показателя асимметрии может быть как положительным, так и отрицательными характеризовать направление отклонения. Положительная величина показателя свидетельствует о правосторонней асимметрии, и при этом соблюдается следующее соотношение:МеМо.Левостороннюю асимметрию характеризуют отрицательное значение показателя и соотношение средних: МеМо.

Методы расчета ассиметрии: - Исходя из соотношения средних величин

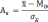- Метод ЛиндбергаN - удельный вес статистической совокупности таких наблюдений, чьи индивидуальные признаки больше средней арифметической простой величины.

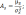
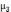- метод центральных моментов третьего порядка - центральный момент третьего порядка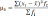

Оценка показателей ассиметрии на значимость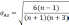

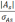Если отношение больше 3,тогда асимметрия признается значимой, а само распределение показательным; если меньше 3–не существенной

Показатели Экцесса – характеризуют отклонение реального распределения от нормального вверх, вниз. Отрицательное значение эксцесса свидетельствует о плосковершинности распределения и близости его к равномерному, положительное значение характеризует островершинность распределения и очень небольшую колеблемость признака в совокупности.

- метод Линдберга Ex=n-0,389

Где n - удельный вес кол-ва наблюдений, находящихся в интервале 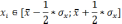- метод центрального момента 4 порядка