
- •Глава I. Метод координат на плоскости.
- •Глава II. Прямая на плоскости.
- •Глава III. Векторное и смешанное произведения.
- •Глава IV. Плоскость в пространстве.
- •Глава V. Прямая в пространстве.
- •Глава VI. Метрические задачи на сочетание
- •Глава VII. Кривые второго порядка на плоскости.
- •Системы координат
- •§ 2. Полярная система координат на плоскости
- •§3. Декартова система координат в пространстве
- •§4. Цилиндрическая система координат в пространстве
- •§5. Сферическая система координат в пространстве
- •Аналитическая геометрия Линии на плоскости
- •Линии первого порядка. Прямые на плоскости.
- •Угол между прямыми
- •Общее уравнение прямой
- •Неполное уравнение первой степени
- •Уравнение прямой “в отрезках”
- •Совместное исследование уравнений двух прямых
- •Нормаль к прямой
- •Угол между двумя прямыми
- •Каноническое уравнение прямой
- •Параметрические уравнения прямой
- •Нормальное (нормированное) уравнение прямой
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Примеры задач на тему «прямая на плоскости»
- •Векторное произведение векторов
- •Свойства векторного произведения Геометрические свойства
- •Алгебраические свойства
- •Выражение векторного произведения через координаты сомножителей
- •Смешанное произведение трёх векторов
- •Геометрический смысл смешанного произведения
- •Выражение смешанного произведения через координаты векторов
- •Примеры решения задач по теме: «Векторная алгебра».
- •Поверхности в пространстве
- •Плоскость
- •Неполные уравнения плоскости
- •Уравнение плоскости в «отрезках»
- •Угол между плоскостями
- •Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой
- •Нормальное уравнение плоскости. Расстояние от точки до плоскости.
- •Расстояние от точки до плоскости
- •Приведение общего уравнения плоскости к нормальному виду
- •Примеры задач на тему «Плоскость».
- •Линии в пространстве. Прямая в пространстве
- •Канонические уравнения прямой в пространстве
- •Параметрические уравнения прямой
- •Уравнения прямой, проходящей через две заданные точки
- •Угол между двумя прямыми в пространстве
- •Угол между прямой и плоскостью
- •Условие принадлежности двух прямых одной плоскости
- •Некоторые задачи на построение прямых и плоскостей
- •Примеры решения задач по теме «Аналитическая геометрия»
- •Кривые второго порядка
- •Пример приведения общего уравнения линии второго порядка к каноническому виду
- •Вывод уравнения эллипса
- •Гипербола
- •Парабола
- •Примеры решения задач на тему «Кривые второго порядка».
Свойства векторного произведения Геометрические свойства
Векторное произведение
 равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
равно нулю тогда и только тогда, когда
эти векторы коллинеарны:
![]() ||
||![]() .
.
Доказательство.
Пусть угол между векторами
![]() и
и![]() равен
равен![]() .
.
a)
Докажем, что
![]() .
.
![]() или
или
![]() 1800
1800
![]() .
.
б)
Докажем, что
![]() .
.
![]()
если
![]()
![]() .
.
Если
![]() ,
или
,
или![]() .
.![]()
Модуль векторного произведения
 равен площади параллелограмма,
построенного на этих векторах.
равен площади параллелограмма,
построенного на этих векторах.
Доказательство.
Из курса геометрии
![]()
Из
свойства 2 следует, что
![]() ,
где
,
где![]() – единичный вектор, перпендикулярный
векторам
– единичный вектор, перпендикулярный
векторам![]() и
и![]() и
образующий с ними правую тройку:
и
образующий с ними правую тройку:
а)
![]() =1,
=1,
б)
![]() ,
,![]() ,
,
в)
![]() ,
,![]() ,
,![]() – правая тройка.
– правая тройка.
Алгебраические свойства
Антикоммутативность:
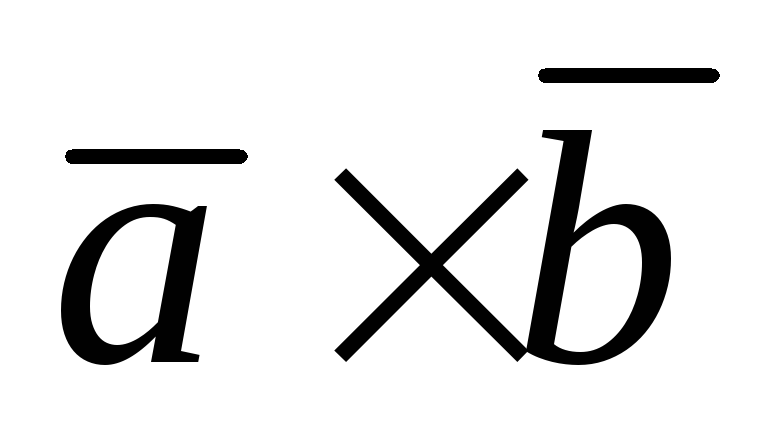 =
=

Доказательство.
Модули векторов
![]() и
и![]() равны по определению векторного
произведения. Проверим их направление:
равны по определению векторного
произведения. Проверим их направление:
а)
![]() ||
||![]()
![]() равенство выполняется;
равенство выполняется;
б)
![]() и
и![]() не
параллельны. Но
не
параллельны. Но![]() ||
||![]() по определению векторного произведения,
тогда либо
по определению векторного произведения,
тогда либо![]() ,
либо
,
либо![]() .
Пусть
.
Пусть![]() ,
а
,
а![]() .
Тройка векторов
.
Тройка векторов![]() правая, а тройка
правая, а тройка![]() – левая. Следовательно,
– левая. Следовательно,![]() и
и
![]() =
=
![]() .
.
Ассоциативность относительно умножения на число.
![]()
![]()
проверяем модуль:
а)![]() ,
,![]() ,
,
где
![]() – угол между векторами
– угол между векторами![]() и
и![]() ,
а
,
а![]() – угол между векторами
– угол между векторами![]() и
и![]() .
.
![]() =>
=>
![]()
поверяем направление:
б)
если
![]()
![]()
![]()
если
![]()
![]()
![]() и
и
![]()
![]()
![]() .
.
5. Дистрибутивность относительно сложения векторов
![]()
Выражение векторного произведения через координаты сомножителей
Теорема
1. Пусть
векторы
![]() и
и![]() имеют координаты
имеют координаты
![]() .
.
Векторное произведение этих векторов имеет координаты
 . (16)
. (16)
Можно расписать определители:
![]() (16’)
(16’)
или представить в виде
 . (16’’)
. (16’’)
Доказательство. Рассмотрим векторные произведения базисных векторов:
![]()
![]() (17)
(17)
![]() .
.
Разложим
векторы
![]() и
и![]() по базису
по базису![]() :
:
![]()
 .
.
На основании свойств векторного произведения мы можем перемножать правые части почленно:
![]()
с учетом формул (17).
Пример 1. Найти координаты векторного произведения векторов
![]() .
.
Решение.
Пусть
![]() .
.
 .
.
Пример
2: Даны три
точки:
![]() .
.
Найти
площадь треугольника АВС
(![]() ).
).
Решение.
![]() .
.
Найдем
координаты векторов
![]() .
.
![]() .
.
![]() .
.
Смешанное произведение трёх векторов
Даны
при произвольных вектора
![]() .
.
Определение.
Если результат векторного произведения
![]() скалярно умножить на вектор
скалярно умножить на вектор
![]() ,
то
,
то
![]() – это смешанное произведение векторов
– это смешанное произведение векторов
![]() .
.
Геометрический смысл смешанного произведения
Теорема
2. Смешанное
произведение
![]() равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если
равно объему параллелепипеда, построенному
на приведённых к общему началу векторах,
взятому со знаком <+>, если
![]() –
правая тройка векторов, и со знаком <->,
если тройка
–
правая тройка векторов, и со знаком <->,
если тройка![]() –
левая.
–
левая.
Если
векторы
![]() –
компланарны, то объем равен нулю, и
–
компланарны, то объем равен нулю, и
![]() .
.
Доказательство.
Пусть S
– площадь параллелограмма, построенного
на векторах
![]() ,
,
![]() – единичный вектор, перпендикулярный
к векторам
– единичный вектор, перпендикулярный
к векторам
![]() и образующий с ними правую тройку.
(Вектор
и образующий с ними правую тройку.
(Вектор![]() – орт векторного произведения
– орт векторного произведения
![]() .)
.)
Из геометрического свойства 2 векторного произведения
![]() (18)
(18)
![]() –высота
параллелепипеда, построенного на
векторах
–высота
параллелепипеда, построенного на
векторах
![]() ,
с основанием S.
,
с основанием S.
![]() ,
а
,
а
![]() ,
если
,
если
![]() правая тройка, то есть той же ориентации,
что и
правая тройка, то есть той же ориентации,
что и
![]() .
.
![]() ,
а
,
а
![]() ,
если тройка
,
если тройка
![]() левая.
левая.
Если
векторы
![]() –
компланарны, то
–
компланарны, то
![]() .
.
Следствие
1.
![]() .
.
Доказательство. Скалярное произведение векторов коммутативно, следовательно
![]() .
.
По
теореме 2:
![]() ,
,
![]() .
.
Далее
будем обозначать смешанное произведение
![]() ,
так как
,
так как
![]() .
.
Следствие 2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны.
Выражение смешанного произведения через координаты векторов
Теорема
3.
Пусть векторы
![]() имеют в ортонормированном базисе
координаты
имеют в ортонормированном базисе
координаты
![]() .
Тогда смешанное произведение этих
векторов можно представить в виде
.
Тогда смешанное произведение этих
векторов можно представить в виде
 .
.
Доказательство.
![]() .
.
По теореме о векторном произведении:
 .
.
Умножим
векторное произведение скалярно на
вектор
![]() :
:
 .
.
По следствию 2 необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат векторов:
 компланарны.
компланарны.
Пример
3. Даны четыре точки:
![]() .
Найти объем тетраэдраАВСD.
.
Найти объем тетраэдраАВСD.
Решение. Объем тетраэдра равен одной шестой объема параллелепипеда с теми же основанием и высотой:
![]() .
.
Координаты
векторов
![]() .
.
По теореме 3
 .
.
