Линии в пространстве. Прямая в пространстве

В аналитической геометрии каждая линия рассматривается как пересечение двух поверхностей и соответственно определяется заданием двух уравнений.

Пусть F₁(x, y, z)=0 и F₂(x, y, z)=0 – уравнения двух поверхностей.

Система уравнений определяет линию, являющуюся их пересечением.

Следовательно, прямую можно задать системой двух уравнений плоскостей:

(1)

Это возможно только в том случае, когда плоскости не совпадают и не параллельны, т.е. когда нормали ₁=и₂=не коллинеарны.

Система (1) – это общее уравнение прямой в пространстве.

Через каждую прямую проходит бесконечное множество плоскостей (пучок плоскостей).

Определение. Cовокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей с центром в L.

Умножим уравнения системы (1) соответственно на коэффициенты и, одновременно не равные нулю.

–уравнение плоскости, проходящей через прямую L.

(Докажите самостоятельно аналогично доказательству для пучка прямых)

Определение. Совокупность всех плоскостей, проходящих через данную точку , называетсясвязкой плоскостей с центром в точке M₀.

Канонические уравнения прямой в пространстве

Пусть – направляющий вектор прямойL, а – точка, принадлежащая прямой. Пусть– точка с переменными координатами.

Чтобы точка принадлежала прямойL, вектор должен быть коллинеарным вектору:

. (2)

Уравнения (2) – это канонические уравнения прямой в пространстве. Пусть прямая L задана общим уравнением:

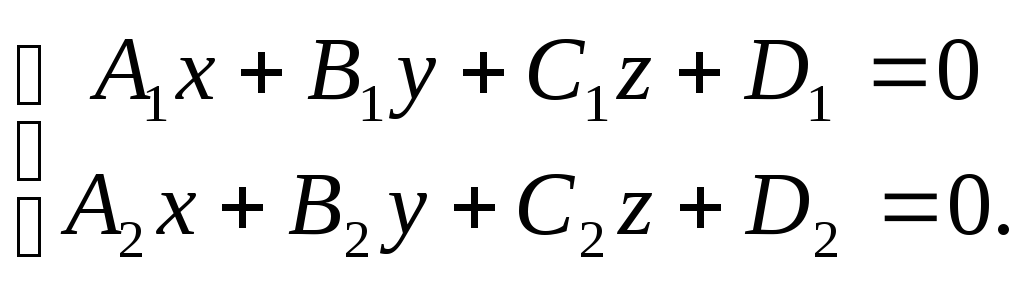
Найти канонические уравнения прямой L.

1). Найдем точку . Для этого нужно задать одну из координат, а две другие определить из решения системы (1).

2). Найдем направляющий вектор прямой .

и и.

, по определению векторного произведения

.

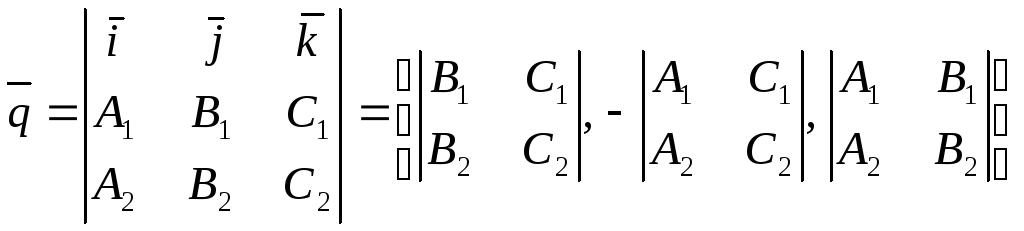Зная координаты точки, принадлежащей прямой, и координаты ее направляющего вектора, можно составить канонические уравнения прямой в виде (2).

Параметрические уравнения прямой

Получаются из канонических уравнений прямой. Пусть

.

Тогда можно записать три уравнения:

(3)

Система (3) – это параметрические уравнения прямой L, проходящей через точку и имеющей направляющий вектор. Параметрические уравнения прямой имеют физический смысл: они описывают движение точки вдоль заданной прямой из начального положения, где– проекции вектора скорости точки на координатные оси.

Уравнения прямой, проходящей через две заданные точки

Пусть заданы две точки, лежащие на прямой: и.

В качестве направляющего вектора прямой можно взять вектор :

.

Подставляем в канонические уравнения (2) координаты одной из точек, например М₁, и координаты направляющего вектора:

. (4)

Получили уравнения прямой, проходящей через две заданные точки.

Угол между двумя прямыми в пространстве

Определение угла между двумя прямыми сводится к определению угла между их направляющими векторами:

(5)

Составьте самостоятельно условие параллельности и перпендикулярности прямых в пространстве.

Угол между прямой и плоскостью

Пусть заданы плоскость :Ax + By + Cz + D = 0

и прямая L: .

Пусть - угол между нормалью к плоскости₁=и направляющим вектором прямой. Тогда уголмежду плоскостьюи прямойL - дополнительный к этому углу: . Тогда

. (6)

1). Условие параллельности прямой и плоскости: =0

2). Условие перпендикулярности прямой и плоскости:

3). Условие принадлежности прямой плоскости. Пусть – любая точка прямой. Чтобы прямая лежала в плоскости должны выполняться два условия:

а) направляющий вектор прямой должен быть перпендикулярен нормали к плоскости:

=0,

б) произвольная точка прямой должна лежать в плоскости:

.