
teorija_mehanizmov_i_mashin_belanov_savenkov
.pdf
71
нерухомої вісі. Прикладами такого машинного агрегату можуть слугувати електродвигун, з’єднаний з відцентровим насосом, турбіна (парова, газова, водяна), яка з’єднана з генератором і т.д. Як відомо із теоретичної механіки, рівняння руху у цьому випадку можна написати у вигляді:
I |
dщ |
=T |
(3.8), |
|
|||
|
dt |
|
|
де I – момент інерції обертаючої ланки відносно вісі обертання; Т – різниця |
|||
моментів рушійних сил і корисних сил опору |
(T =Tp −Tk ) відносно вісі |
||
обертання.
В праву частину рівняння (3.8) входять моменти рушійних сил Тр і корисних сил опору Топ; які можуть бути функціями переміщення (кута φ), швидкості (ω), або часу (t).
Тоді можна мати
I ddщt =Tp (щ)−Toп (щ),
I ddщt =Tp (ϕ)−Toп (ϕ),
I ddщt =Tp (t)−Toп (t).
Рівняння (3.9) приводиться до вигляду:
tk |
щk |
dщ |
|
|
||
∫dt =I ∫ |
|
|
. |
|||
T |
(щ)−T |
(щ) |
||||
t |
0 |
щ p |
oп |
|
|
|
|
0 |
|
|
|
|
|
Проводячи інтегрування, знаходимо
щk |
dщ |
|
|
|
tk = t0 + I ∫ |
|
|
. |
|
T |
(щ)−T |
(щ) |
||
щ p |
oп |
|
|
|
0 |
|
|
|
|
За повторним інтегруванням, визначимо закон руху ϕ =ϕ(t)
dщ |
|
ϕ |
t |
|
||
= щ(t); |
∫k |
dϕ =∫k |
щ(t)dt |
|||
dt |
|
|||||
|
ϕ0 |
t0 |
|
|||
|
|
|
|
|||
(3.9)
(3.10)
(3.11)
(3.12)
(3.13)
(3.14)
|
72 |
tk |
|
і далі ϕk =ϕ0 + ∫щ(t)dt . |
(3.15). |
t0 |
|
Для розв’язання рівняння (3.10) його ліву частину помножимо і розділимо на dφ:
|
|
I |
dщ |
|
dϕ |
=T |
p |
(ϕ)−T |
(ϕ) |
, |
|
|
|
|
|||||||
|
|
|
dϕ |
|
dt |
oп |
|
|||
|
|
|
|
|
|
|
|
|||
звідки маємо |
Iщ dщ= [Tp (ϕ)−Toп (ϕ)]dϕ |
|
|
|
|
|||||
щ |
ϕ |
[Tp (ϕ)−Toп (ϕ)]dϕ . |
|
|
|
|
||||
і далі I ∫k |
щdщ=∫k |
|
|
|
|
|||||
щ0 |
ϕ0 |
|
|
|
|
|
|
|
|
|
Інтегруючи, одержимо:
I щк2 −що2 = ϕ∫k [Tp (ϕ)−Toп (ϕ)]dϕ . 2 ϕ0
(3.16)
(3.17)
Вираз (3.17) є рівнянням руху механізму машинного агрегату у формі рівняння кінетичної енергії. Із рівняння (3.17)
ϕk
щк = 2I ∫[Tp (ϕ)−Toп (ϕ)]dϕ +щo2 . (3.18)
ϕ0
Знаючи щ= щ(ϕ), для визначення часу руху машинного агрегату
скористаємося залежністю |
щ= |
dϕ |
. Тоді |
dϕ |
= щ(ϕ), звідки |
|
|||||
dt |
|
dt |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
t |
ϕ |
|
dϕ |
|
|
|
||
|
|
|
∫k |
dt =∫k |
|
. |
|
(3.19) |
|||
|
|
|
|
щ(ϕ) |
|||||||
|
|
|
t0 |
ϕ0 |
|
|
|
|
|
|
|
Після інтегрування |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
dϕ |
|
|
||
|
|
|
tk |
= t0 +ϕ∫k |
. |
(3.20) |
|||||
|
|
|
щ(ϕ) |
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
73
Таким чином, закон руху ϕ =ϕ(t) |
знайдено. |
|
||||||||||
В рівнянні (3.11) змінні розділяються одразу: |
|
|||||||||||
|
|
|
щ |
|
|
t |
|
|
|
|
||
|
|
I ∫k dщ=∫k [Tp (t)−Toп (t)]dt . |
(3.21) |
|||||||||
|
|
|
щ0 |
|
|
t0 |
|
|
|
|
||
|
щ = щ + |
1 tk |
[T |
|
(t)−T |
(t)]dt |
|
|
||||
|
|
|
|
|
|
|||||||
Звідки |
I ∫ |
p |
. |
(3.22) |
||||||||
k |
o |
|
|
oп |
|
|||||||
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
Одержавши |
залежність |
|
щ= щ(t) |
і |
замінюючи |
ω його значенням |
||||||
щ= |
dϕ |
, одержимо |
dϕ |
= щ(t). |
|
dt |
dt |
||||
|
|
|
Після повторного інтегрування визначимо закон руху:
ϕ∫k dϕ =t∫k щ(t)dt ,
ϕ0 t0
tk
звідки ϕk =ϕ0 + ∫щ(t)dt .
t0
(3.23)
(3.24)
§ 3.3. Приведення мас і сил до ланки приведення
Для визначення закону руху ланок механізмів складного машинного агрегату з однією ступінню рухомості зручно скористатися методом приведенням мас і сил, завдяки якому складний механізм замінюють еквівалентним йому простим, який має одну рухому ланку – ланку приведення. Одержане рішення переносять на початкову систему. Приведення мас проводять за умови рівності суми кінетичних енергій ланок початкової системи кінетичній енергії ланки приведення
n |
|
∑Ki = Kn |
(3.25) |
i=1 |
|
n |
|
де ∑Ki - сума кінетичних енергій ланок механізму; Kn |
- кінетична енергія |
i=1 |
|
ланки приведення.

74
Кінетична енергія ланки, яка робить плоско-паралельний рух,
визначається рівнянням: |
I щ2 |
|
m х2 |
|
|
|
Ki = |
+ |
|
|
|||
i i |
i i |
, |
(3.26) |
|||
2 |
2 |
|||||
|
|
|
|
де Ii – момент інерції ланки і відносно вісі, яка проходить через центр ваги; ωi – кутова швидкість ланки i; mi – маса ланки i; υi – швидкість центра ваги ланки i.
При поступальному русі кінетична енергія ланки приведення визначається рівнянням
= m х2
Kn n n ,
2
|
Kn = In |
щ2 |
|
|
при обертальному русі |
n |
, |
||
2 |
||||
|
|
|
де mn – приведена маса механізму; υn – швидкість ланки приведення; приведений момент інерції відносно вісі обертання ланки приведення; кутова швидкість ланки приведення.
Підставивши значення Ki і Kn в рівняння (3.25), знаходимо
(3.27)
(3.28)
In –
ωn –
n |
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||
|
щi |
|
|
miхi |
|
|
|
mnхn |
|
|
|
|||||
∑ Ii |
|
|
|
+ |
|
|
|
= |
|
|
, |
|
(3.29) |
|||
2 |
|
|
2 |
|
2 |
|
|
|||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|||
|
|
щi |
|
|
|
miхi |
|
|
|
щn |
|
|
||||
∑ Ii |
|
|
|
|
+ |
|
|
|
|
= In |
|
|
. |
(3.30) |
||
2 |
|
|
2 |
|
|
2 |
||||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Розв’язуючи рівняння (3.29) і (3.30) відносно mn і In, одержимо вирази для визначення приведеної маси і приведеного моменту інерції:
mn
In
n |
|
|
|
щi |
|
2 |
|
хi |
|
2 |
|
|
|||||
= ∑ |
|
|
|
|
|
|
|
|
, |
||||||||
|
|
|
|
|
|||||||||||||
|
Ii |
х |
|
|
|
+mi |
х |
|
|
|
|
||||||
i=1 |
|
|
n |
|
|
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
n |
|
|
|
щi |
2 |
|
|
хi |
|
2 |
|
|
|||||
= ∑ |
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
Ii |
щ |
|
|
+mi |
щ |
|
|
|
||||||||
i=1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
|
|
n |
|
|
||||||||
(3.31)
(3.32)
Таким чином, приведеною масою називають умовну масу, яка має швидкість ланки приведення і наділена у кожному фіксованому положенні кінетичною енергією початкового механізму.
75
Приведеним моментом інерції називають момент інерції фіктивного твердого тіла, який обертається навколо нерухомої вісі з кутовою швидкістю ланки приведення і наділена в кожному фіксованому положенні кінетичною енергією початкового механізму. Із рівнянь (3.31) і (3.32) виходить, що величини приведеної маси і приведеного моменту інерції залежать від квадрату відношення швидкостей. Отже, в загальному випадку ці величини є змінними, які залежать від положення механізму. В окремому випадку, коли передаточне відношення кінематичних ланцюгів механізму сталі, приведена маса і приведений момент інерції також сталі.
Приведення сил і моментів проводять за умови рівності суми елементарних робіт всіх сил і моментів, діючих на ланки початкового механізму, елементарній роботі приведеної сили, або приведеного моменту. При розрахунках елементарні роботи сил і моментів замінюють потужностями. Математично це можна виразити так:
n |
|
∑Рi = Рn , |
(3.33) |
i=1
n
де ∑Рi - сума потужностей сил і моментів, діючих на ланки початкового
i=1
механізму; Рn - потужність приведеної сили, або приведеного моменту.
Якщо ланка приведення рухається поступально, то усі сили і моменти, діючі на ланки механізму, зручно приводити до сили. В цьому випадку
Рn = Fnхn ,
де Fn - приведена сила; хn - швидкість ланки приведення.
Якщо ланка приведення обертається, то усі сили і моменти, діючі на ланки механізму, зручно приводити до моменту. Тоді
Рn =Tnщn ,
де Tn - приведений момент; щn - кутова швидкість ланки приведення.
У загальному випадку на кожну ланку механізму може діяти і сила, і момент, через це
Рi |
=Tiщi + Fiхi cos гi , |
(3.34) |
де Ti - момент, діючий на ланку i; |
щі - кутова швидкість ланки і; Fі |
- сила, |
діюча на ланку і; хі - швидкість центра ваги ланки і; γі – кут між напрямком сили і швидкості.
|
76 |
|
|
Підставивши значення Рi |
і Рn в рівняння (3.33), знаходимо |
|
|
∑n (Ti щi |
+ Fiхi |
cos гi )= Fnхn , |
(3.35) |
i=1 |
|
|
|
∑n (Ti щi |
+ Fiхi |
cos гi )=Tnщn . |
(3.36) |
i=1 |
|
|
|
Розв’язуючи рівняння (3.35) і (3.36) відносно Fn і Tn , одержимо вирази для визначення приведеної сили і приведеного моменту:
n |
|
|
щi |
|
|
|
хi |
|
|
|
Fn = ∑ Ti |
|
|
+ Fi |
|
|
cos гi , |
(3.37) |
|||
|
хn |
|
|
хn |
||||||
i=1 |
|
|
|
|
|
|
|
|
||
n |
|
щi |
|
|
хi |
|
|
|
||
Tn = ∑ |
Ti |
+ Fi |
|
cos гi . |
(3.38) |
|||||
щn |
щn |
|
||||||||
i=1 |
|
|
|
|
|
|
||||
Таким чином, приведеною силою називають умовну силу, прикладену до ланки приведення, елементарна робота якої в кожному фіксованому положенні дорівнює сумі елементарних робіт сил і моментів, діючих на ланки початкового механізму.
Приведеним моментом називають умовний момент, прикладений до обертаючої ланки приведення, елементарна робота якого в кожному фіксованому положенні дорівнює сумі елементарних робіт сил і моментів, діючих на ланки початкового механізму.
Із рівнянь (3.37) і (3.38) видно, що величини приведеної сили і приведеного моменту залежать від величини сил і моментів, діючих на ланки початкового механізму, а також від відношення швидкостей, тобто від передаточних відношень між окремими ланками початкового механізму і ланкою приведення.
В результаті введення понять приведеної маси mn, приведеного моменту інерції In, приведеної сили Fn і приведеного моменту Tn рівняння
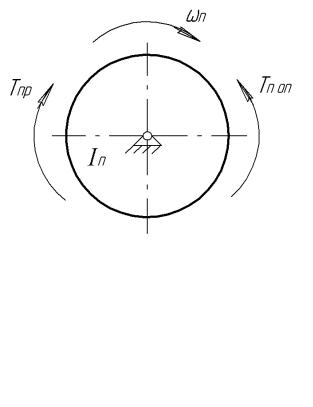
руху багатоланкового машинного агрегату (в формі рівняння кінетичної енергії) можна написати як рівняння руху одноланкового механізму, який має приведену масу і приведений момент інерції такий, що находиться під дією приведеної сили, чи приведеного моменту (рис. 3.12, рис. 3.13), тобто рівняння
n |
n |
n tk |
|
∑Kik −∑Kio = ∑∫Pi dt |
(3.39) |
||
i=1 |
i=1 |
i=1 t0 |
|
77
можна замінити рівнянням
|
щ |
2 |
|
|
|
2 |
|
|
ϕnk |
|
||
Ink |
|
|
− Ino |
щ |
= ∫Tn dϕ |
|
||||||
|
nk |
|
|
no |
(3.40) |
|||||||
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ϕno |
|
(ланка приведення обертається), або |
|
|
|
|
|
|
|
|
||||
|
|
хnk2 |
|
|
|
хno2 |
Snk |
|
||||
M nk |
|
|
|
−M no |
|
|
|
= ∫Fn dS |
(3.41) |
|||
|
2 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Sno |
|
(ланка приведення рухається поступально).
Тут Kiк , Kiо і Рі – відповідно кінетичні енергії і потужність ланки і в положеннях К і О; Ink , Ino , M nk , M no - приведені моменти інерції і приведені маси в положеннях К і О ланки приведення.
Tn =Tnp −Tn.on; Fn = Fnp − Fn.on , |
|
де Tnp і Tn.on - приведені моменти рушійних сил і сил опору відповідно; |
Fnp і |
Fn.on - приведені рушійні сили і сили опору відповідно. |
|
Рисунок 3.12 – Ланка приведення рухається поступально
Рисунок 3.13 – Ланка приведення обертається

78
Для визначення закону руху ланки приведення у багатьох випадках користуються рівнянням кінетичної енергії в диференціальній формі. Для його одержання, диференціюємо за часом рівняння (3.40), вважаючи, що In є функція кута обертання φn ланки приведення:
|
|
Inщn |
dщn |
+ |
1 |
|
щn2 |
|
dIn |
|
dϕn |
=Tn |
dϕn |
. |
||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
dt |
2 |
|
|
|
dϕn |
|
|
dt |
dt |
||||||
Оскільки |
dϕn |
= щn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Inщn |
dщn |
|
+ |
1 |
щn3 |
dIn |
=Tnщn . |
|||||||||
|
|
|
dt |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
dϕn |
|
|
||||||||
Скорочуючи на щn , одержимо
I |
|
dщn |
+ |
1 |
щ2 |
dIn |
=T |
. |
(3.42) |
|
|
2 |
|
||||||
|
n |
dt |
n dϕn |
n |
|||||
Рівняння (3.42) називають диференціальним рівнянням руху машинного агрегату.
В механізмах, де ланки мають тільки обертальний рух, передаточне
|
|
щi |
|
|
|
відношення |
|
|
кінематичних ланцюгів сталі, а отже, сталі і їх |
||
|
|||||
uin = |
щ |
||||
|
|
n |
|
||
приведені маси і приведені моменти інерції. Для таких механізмів рівняння (3.40) і (3.42) запишуться наступним чином:
|
2 |
2 |
|
ϕnk |
|
In |
щnк −щnо |
|
= ∫Tпdϕ; |
(3.43) |
|
|
|||||
|
2 |
|
|
ϕno |
|
|
|
|
|
|
|
|
In |
dщn |
=Tп . |
(3.44) |
|
|
dt |
||||
|
|
|
|
||
Ці рівняння співпадають з рівняннями (3.8) і (3.17), написаних для тіла, який робить обертальний рух. Якщо диференціювати за часом рівняння (3.41), вважаючи, що mn є функцією переміщення Sn ланки приведення, то одержимо:
mnхn ddхtn + 12 хn2 dmdSn dSdt = Fn dSdtn .
79
Оскільки |
dSn |
= хn , |
|
dt |
|||
|
|
mnхn |
dхn |
+ |
1 |
хn3 |
dmn |
= Fnхn. |
(3.45) |
|
2 |
|
|||||
|
dt |
|
dS |
|
|||
Скорочуючи на хn , одержимо
m |
n |
dхn |
+ |
1 |
х2 |
dmn |
= F |
. |
(3.46) |
|
|
|
|||||||
|
dt |
2 |
n |
dS |
n |
||||
|
|
|
|
|
|
||||
Рівняння (3.46) називають диференціальним рівнянням руху машинного агрегату.
Якщо приведена маса залишається величиною сталою, незалежної від
положень механізму, то |
dmn |
= 0 і рівняння (3.46) приймає вигляд |
|
||||
dS |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mn |
dхn |
= Fп |
, |
(3.47) |
|
|
dt |
|||||
|
|
|
|
|
|
|
|
яке зовнішньо не відрізняється від рівняння прямолінійного руху матеріальної точки.
§ 3.4. Стадії руху машинного агрегату
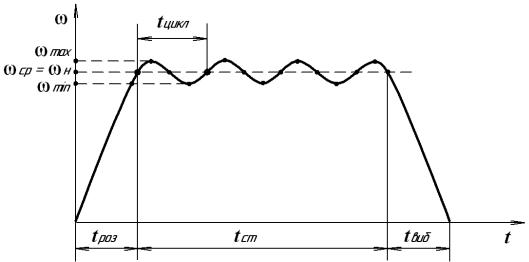
Вроботі кожного машинного агрегату можна виділити три стадії руху: розгін, сталий рух і вибіг (рис.3.14).
Встадії розгону робота рушійних сил більше роботи сил опору. За рахунок цієї різниці робіт швидкість ланок змінюється від нуля до номінального значення.
Встадії сталого руху в залежності від виду механічних характеристик двигуна і технологічної машини швидкість ланок постійна, або змінюється циклічно, тобто її значення повторюються через визначений відрізок часу – цикл.
80
Рисунок 3.14 – Стадії руху машинного агрегату
Із цього виходить, що за термін циклу приріст кінетичної енергії дорівнює нулю і робота рушійних сил дорівнює роботі сил опору.
Величину коливань швидкості в стадії сталого руху характеризують коефіцієнтом нерівномірності ходу:
|
|
|
д= |
ωmax −ωmin |
, |
(3.48) |
|
|
|
|
|
||||
|
|
|
|
ωср |
|
|
|
де |
ωср = ωmax +ωmin |
- |
середня швидкість. |
Значення середньої |
швидкості |
||
|
2 |
|
|
|
|
|
|
приймається за номінальну швидкість у сталому режимі. |
|
||||||
|
Для багатьох машин задається допустима величина коефіцієнта |
||||||
нерівномірності ходу |
[д]. В цьому випадку при динамічних розрахунках |
||||||
необхідно перевірити умову д≤ [д]. |
|
|
|
||||
|
Для машинних агрегатів, які мають сталий приведений момент інерції |
||||||
(In = const), коефіцієнт |
нерівномірності |
ходу рахують за |
формулою, |
||||
одержаною із рівнянь (3.48) і (3.43), записаних для відрізка шляху, або часу, відповідно зміні швидкості від максимального значення до мінімального:
|
2 |
2 |
|
ϕωmax |
In |
ωmax −ωmin |
= |
∫Tn (ϕ)dϕ . |
|
|
2 |
|||
|
|
|
ϕωmax |
|
|
|
|
|
|
Помножимо чисельник і знаменник рівняння (3.48) на ωср
замінимо її значенням ωср = |
ωmax +ωmin : |
|
2 |
(3.49)
і в знаменнику ωср
