
teorija_mehanizmov_i_mashin_belanov_savenkov
.pdf
131
При t = 2t′ швидкість сягає максимальної величини (рис. 5.8, б)
υ =υmax = |
1 |
amaxtв +amax |
t |
в |
− |
1 |
к |
|
t 2 |
= |
3 |
amaxtв − |
1 |
4 |
a |
max |
|
t 2 |
= |
1 |
amaxtв . |
|
|
|
|
|
в |
|
|
|
|
в |
|
||||||||||||
8 |
4 |
2 |
16 |
8 |
2 |
tв |
16 |
4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
При t = t′′ = 3t′
υ =υ′′ = 81 amaxtв +amax 2t′− 12 к4(t′)2 =
= |
1 |
a |
t |
|
+a |
|
|
2 |
t |
в |
− |
1 |
4 |
a |
max |
4 |
|
t 2 |
= |
1 |
|
a |
|
|
t |
|
; |
|
|
|
|||||||||
|
|
в |
|
|
|
|
|
|
|
|
в |
|
|
|
|
в |
|
|
|
||||||||||||||||||||
8 |
|
|
4 |
2 |
|
|
|
|
16 |
8 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
max |
|
|
max |
|
|
|
|
|
tв |
|
|
|
|
max |
|
|
|
|
|
|||||||||||||||||
S = S′′ = |
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
tв |
|
|
1 |
|
|
|
|
tв2 |
|
1 |
|
amax |
|
tв3 |
||||||||||||
|
amaxtв |
+ |
|
amaxtв 2 |
|
|
+ |
|
|
amax 4 |
|
− |
|
|
4 |
|
|
8 |
|
= |
|||||||||||||||||||
96 |
8 |
4 |
|
2 |
16 |
6 |
|
tв |
64 |
||||||||||||||||||||||||||||||
= 961 amaxtв2 +161 amaxtв2 + 81 amaxtв2 −121 amaxtв2 = 1196 amaxtв2 .
3) При t''< t < tв маємо:
|
a = |
dυ |
|
|
|
′′ |
|
|
||||
|
|
|
|
|
|
|
||||||
|
dt |
= −amax +к(t −t ); |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
υ =υ′′+ ∫t |
adt =υ′′−amax (t −t′′)+ |
|
1 |
к(t −t′′)2 ; |
||||||||
2 |
||||||||||||
|
t′′ |
|
|
|
|
|
|
|
|
|||
S = S′′+ ∫t |
υdt = S′′+υ′′(t −t′′)− |
1 |
amax (t |
−t′′)2 + |
1 |
к(t −t′′)3 . |
||||||
2 |
6 |
|||||||||||
t′′ |
|
|
|
|
|
|
|
|
|
|||
При t = 4t′ = tв (рис. 5.8, в)
132
S = S |
|
|
= |
11 |
|
a |
|
|
|
t 2 |
+ |
1 |
|
a |
|
|
t |
|
|
t |
в |
|
|
− |
1 |
|
a |
|
|
|
t 2 |
+ |
1 |
4 |
a |
max |
|
t3 |
= |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
в |
|||||||||||||||||||||||||||
|
|
96 |
|
|
|
|
8 |
|
|
|
|
|
4 |
|
|
2 |
|
max 16 |
6 |
tв |
64 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
max |
|
|
|
|
|
max в |
|
|
|
|
max |
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= |
|
12 |
a |
|
t 2 |
= |
1 |
a |
|
|
t 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
96 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
max в |
|
|
|
|
max |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
amax |
= |
|
8 |
Smax |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
υ = |
1 |
a |
|
|
t |
|
−a |
|
|
|
t |
в |
|
|
+ |
1 |
|
4 |
|
a |
max |
|
|
t 2 |
= 0; |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
4 |
|
2 |
|
|
|
tв |
16 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
υ |
max |
= |
1 |
a |
max |
t |
в |
|
|
= |
|
|
1 |
t |
в |
8 |
Smax |
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υmax = 2 |
Smax |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
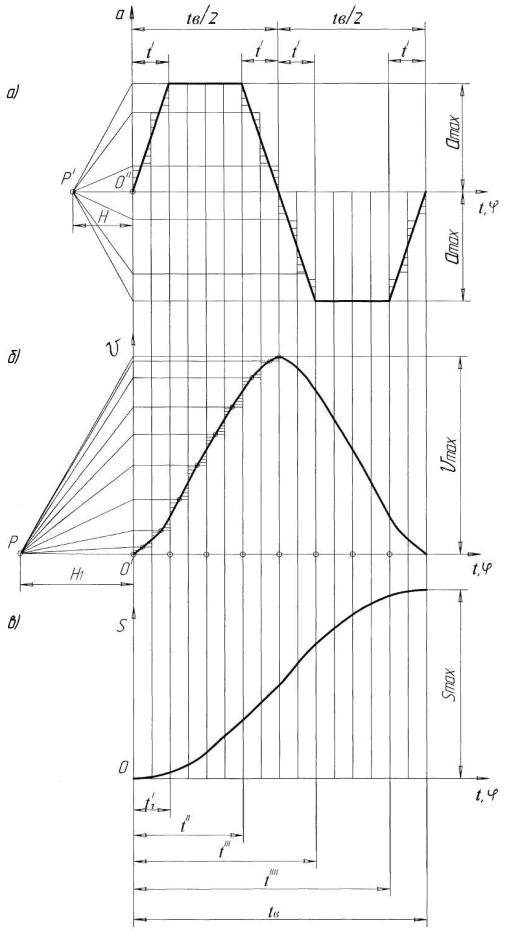
3. Діаграма прискорень – дві рівні рівнобокі трапеції (рис. 5.9, а)
Прискорення, швидкості і переміщення веденої ланки мають різні аналітичні вираження для кожного з п’яти інтервалів часу, відповідних п’ятьом
відрізкам ламаної, яка зображає діаграму прискорень. Нехай t′ =ξtв , тоді
|
|
|
tв |
tв |
(1−4ξ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t′′−t′ |
= |
|
−2t′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
2 |
|
|
|
|
dυ |
|
|
|
|
|
|
|
amax |
|
amax |
|
|
1 |
|
|
|
|||||
|
|
|
1) При |
0 < t < t' маємо |
a = |
= кt , де |
|
к = |
= |
; |
υ = |
кt |
2 |
; |
|||||||||||||
|
1 |
|
dt |
|
t′ |
ξtв |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S = |
кt3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
При t = t′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
υ =υ |
′ = |
1 |
|
amax |
(ξtв )2 = |
|
1 |
amaxξtв; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 ξtв |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
S = S′ = |
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
6 amaxξ |
|
|
tв . |
|
|
|
|
|
|
|
|
|
||||||||
133
2) При t'< t < t'' маємо:
a = ddtυ = amax = const,
через це υ =υ′+amax (t −t′), |
S = S |
′ |
′ |
′ |
)+ |
1 |
′ 2 |
|
|||||||
|
+υ (t −t |
2 |
amax (t −t ) . |
||||
|
|
|
|
|
|
|
|
При t = t′′
υ =υ′′ = 12 amaxξtв +amax 12 (1−4ξ)tв = 12 amaxtв (1−3ξ);
S |
= S′′ = |
1 |
amaxξ |
2tв2 + |
1 |
amaxξtв |
|
1 |
(1−4ξ)tв + |
1 |
amax |
1 |
(1 |
−4ξ)tв |
2 |
= |
||||||||||||
6 |
2 |
2 |
|
|
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
= |
1 |
amaxξ2tв2 |
+ |
1 |
amaxξtв2 |
−amaxξ |
2tв2 + |
1 |
amax |
1 |
tв2 |
(1−8ξ + |
16ξ2 ) |
= |
|
|||||||||||||
6 |
4 |
2 |
4 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=− 65 amaxξ2tв2 + 14 amaxξtв2 + 81 amaxtв2 −amaxξtв2 +2amaxξ2tв2 =
=76 amaxξ2tв2 − 43 amaxξtв2 + 81 amaxtв2 ;
S = S′′ = 241 amaxtв2 (28ξ2 −18ξ +3).
3) При t''< t < t''' маємо: |
|
|
||
a = |
dυ |
= amax −к(t −t′′), |
звідки |
|
dt |
||||
|
|
|
||
υ =υ′′+amax (t −t′′)− 12 к(t −t′′)2 ;
S = S′′+υ′′(t −t′′)+ 12 amax (t −t′′)2 − 16 к(t −t′′)3 .
134
Рисунок 5.9 – Діаграми руху штовхача
135
Аналогічно розв’язуються задачі для останніх двох інтервалів. При t = t +t′′ одержуємо
υ =υmax |
= 2 amaxtв (1 |
−3ξ)+amax (t′)− 2 |
ξtв |
(t′) |
= |
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 amax |
2 |
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
amax |
|
|
|
|
|
|
|
|
= |
a |
t |
|
(1−3ξ)+a |
|
ξt |
|
− |
|
ξ |
2t 2 |
= |
|
|
||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
max |
в |
|
|
|
max |
|
в |
|
2 ξtв |
|
в |
|
|
|
||||||
=12 amaxtв − 23 amaxξtв +amaxξtв − 12 amaxξtв =
=−amaxξtв + 12 amaxtв;
υ =υmax = 12 amaxtв (1−2ξ);
S = |
1 |
amax (3 −18ξ +28ξ2 )tв2 + |
1 |
amax (1 |
−3ξ)ξtв2 |
+ |
1 |
amaxξ2tв2 |
− |
1 |
|
amax |
ξ3tв3 = |
24 |
2 |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
6 ξtв |
||||||
= 81 amaxtв2 − 34 amaxξtв2 + 76 amaxξ2tв2 + 12 amaxξtв2 − 32 amaxξ2tв2 + 12 amaxξ2tв2 −
− 16 amaxξ2tв2 = 81 amaxtв2 − 14 amaxξtв2 ;
S = 12 Smax = 18 amaxtв2 (1−2ξ).
Таким чином,
Smax = 14 amaxtв2 (1−2ξ).
На рис. 5.9 (б, в) діаграми (υ,t) і (S,t) одержані шляхом графічного
інтегрування.
Якщо ξ = 0, то
136
υmax = |
1 |
amaxtв і |
Smax = |
1 |
amaxtв2 |
|
2 |
4 |
|||||
|
|
|
|
(результат, одержаний при розгляді випадку 1).
Якщо ξ = |
1 |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
υmax = |
amaxtв |
|
|
|
і |
|
|
Smax |
= |
|
|
amaxtв2 |
|||||||||||||||||||
|
|
|
|
|
|
|
8 |
||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(результат, одержаний при розгляді випадку 2). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Виразимо amax і |
υmax через |
|
Smax : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
amax = |
|
|
4 |
|
|
|
|
|
Smax |
|
|
, |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1−2ξ |
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
υmax |
= |
1 |
amaxtв (1−2ξ)= |
1 |
|
|
|
|
4 |
|
|
|
|
|
Smax |
tв (1−2ξ), |
|||||||||||||||||
|
|
|
|
|
(1−2ξ) |
2 |
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
tв |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
υmax |
|
= 2 |
Smax |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
|
||||
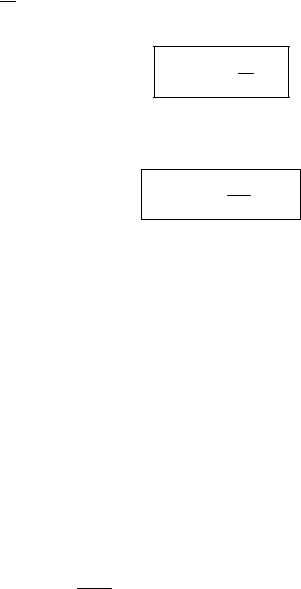
4. Діаграма прискорень – косинусоїда (рис. 5.10, а). |
|||||||||||||||||||||||||||||||||||
Позначивши через amax максимальну |
|
абсолютну величину |
|||||||||||||||||||||||||||||||||
прискорення, маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
а = amax cos кt, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
але при t = tв повинно бути кtв =π, |
звідки к = |
π . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
dυ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πt ; |
|
|
|
|||||||||
|
|
|
|
|
а = |
|
= amax |
cos |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
||
|
|
|
|
|
υ = ∫t |
adt |
|
|
= |
tв |
sin πt amax ; |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
π |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
t |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
S = ∫υdt = |
|
tв |
|
|
|
|
|
|
|
|
|
|
|
|
πt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
π |
2 amax 1−cos |
tв |
. |
|||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

137
Рисунок 5.10 – Діаграми руху штовхача
138
t
При t = 2в (рис. 5.10, б) маємо
υ =υmax = πtв amax .
При t = tв (рис. 5.10, в) маємо
S = Smax = π22 amaxtв2 .
Отже,
|
amax = |
π 2 |
S |
max |
= 4,93 |
|
S |
max |
|
; |
||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
tв |
|
|
|
||||||
υmax = |
amax |
tв = |
π 2 |
Smax |
|
tв |
|
; |
|
|
або |
|||||||||||||
π |
|
|
2 |
2 |
|
|
π |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
tв |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
υmax = |
π |
Smax |
|
=1,57 |
|
Smax |
|
. |
||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
tв |
|
|
|
|
|
|
|
tв |
|
|
|
|
|||||
Як це випадає із одержаних результатів і рис. 5.10 (в), графік переміщень в даному випадку зображує собою косинусоїду, зміщену відносно
вісі абсцис на відстань Smax2 . У відповідності з цим одержаний закон руху називають косинусоїдальним.
5. Діаграма прискорень – синусоїда (рис. 5.11, а)
Аналогічно попередньому
|
а = amax sin кt, |
|
|
|
|
||||||
але при t = tв маємо кtв = 2π, через це к = |
|
2π |
і |
а = amax sin |
2πt |
. |
|||||
|
|
|
|||||||||
Отже, |
|
|
|
|
tв |
|
|
|
tв |
||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
tв |
|
|
|
|
2πt |
|
|
|
|
υ = ∫adt = |
|
|
|
|
|
|
|
||||
|
|
amax 1 |
−cos |
|
; |
|
|
||||
2π |
tв |
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|||

139
Рисунок 5.11 – Діаграми руху штовхача

140
t |
2 |
|
|
|
|
|
|
S = ∫υdt = |
tв |
|
2πt |
|
2πt |
|
|
|
|
amax |
|
−sin |
|
. |
|
4π |
2 |
tв |
tв |
||||
0 |
|
|
|
|
|||
t
При t = 2в (рис. 5.11, б) маємо
υ =υmax = πtв amax .
При t = tв (рис. 5.11, в) маємо
S = Smax = tπв2 amax .
2
Звідси
|
amax |
= 2π |
|
Smax |
= |
6,28 |
Smax |
|
; |
|
|
|
|||
2 |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
tв |
|
|
tв |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
υmax = |
tв |
2π |
|
Smax |
|
, або |
|
υmax = 2 |
Smax |
|
. |
||||
|
|
|
|||||||||||||
|
|
2 |
|
tв |
|||||||||||
|
π |
|
tв |
|
|
|
|
|
|
|
|
|
|||
Хоча одержаний закон руху веденої ланки і називають звичайно синусоїдальним, але крива відстаней не є синусоїда. Ординати S точок цієї
кривої складаються із ординат прямої |
S1 = |
Smaxt |
і ординат синусоїди |
||||||
tв |
|||||||||
|
|
|
|
|
|
|
|
||
S2 |
= |
Smax |
sin |
2πt |
, що можна використати при побудові кривої відстань. |
||||
|
|
||||||||
|
|
2π |
tв |
|
|
|
|||
У всіх розглянутих вище випадків максимальне прискорення і максимальна швидкість штовхача виражаються в залежності від ходу Smax штовхача і часу tв віддалення наступним способом:
amax = ка Smax ;
tв2
υmax = кυ Stmax ,
в
