Алгоритм построения интерполяционного многочлена Ньютона

Для построения интерполяционного многочлена Ньютона необходимо вычислить ряд разделенных разностей, входящих в интерполяционную формулу Ньютона (4.2.5). Но на самом деле, наряду с этими разделенными разностями, придется вычислить и другие разности, которые непосредственно в формулу (4.2.5) не входят, но через которые вычисляются и другие разности нужные нам. Поместим все разделенные разности, необходимые для построения многочлена Ньютона в таблицу. Приведем такую таблицу для случая (табл. 4.1).

Таблица 4.1

Интерполяционный многочлен Ньютона в этом случае примет вид

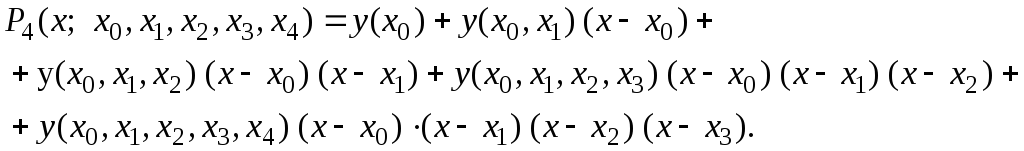
Для построения интерполяционного многочлена Ньютона нам понадобятся только подчеркнутые в табл.4.1 разности, но вычислять необходимо все. Вести вычисления следует слева направо. Вначале вычисляются все разности первого порядка, затем – второго, и так далее.

Пример

Требуется построить для функции интерполяционный многочлен Ньютона третьего порядка с узлами .

Требуемый интерполяционный многочлен Ньютона имеет вид

Пользуясь определением, вычислим значения разделенных разностей и поместим их в табл. 4.2

,

,

,

,

_,

.

Таблица 4.2

Осталось составить интерполяционный многочлен

.

Построенный интерполяционный многочлен в рассмотренном примере совпал с исходной функцией . Это не случайно и непосредственно следует из единственности интерполяционного многочлена.

4.3. Кратные узлы интерполяции. Интерполяционный многочлен Эрмита Кратные узлы интерполяции. Формулировка задачи интерполяции с кратными узлами

Иногда оказываются известными значения функции в заданных точках и значения ее производных. Эту дополнительную информацию можно использовать при построении интерполяционного многочлена. В результате чего получается интерполяционный многочлен Эрмита.

Пусть заданы табличные значения функции и ее производных в заданных точках, причем известными считаются значения

_(4.3.1)

_{…………………………….}

Здесь ,. Введем величину

. (4.3.2)

Будем искать алгебраический многочлен n-й степени такой, что

_(4.3.3)

_{………………………………………….…………………………..}

Точки называютсяузлами интерполяции, а искомый многочлен  интерполяционным многочленом Эрмита.

Если , то узелназываетсяпростым, или однократным, а если , то узелназываетсякратным, причем величина называетсякратностью узла .

Условия (4.3.3) называются условиями интерполяции с кратными узлами.

В дальнейшем будем использовать для многочлена Эрмита, наряду с введенным кратким обозначением, развернутое обозначение. В нем указываются узлы интерполяции в качестве параметров, причем количество повторений узла в обозначении многочлена Эрмита совпадает с его кратностью:

. (4.3.4)

Теорема. Может существовать только один многочлен Эрмита.

Доказательство. Доказательство будем вести от противного. Пусть существуют два разных алгебраических многочлена n-й степени и, удовлетворяющие условиям интерполяции (4.3.3). Тогда их разностьбудет представлять собой алгебраический многочлен степени не вышеn, не равный тождественно нулю, причем для него будут выполнены условия

_(4.3.5)

_{………………………………………….…..}

Таким образом, многочлен имеетm корней суммарной кратности . Полученное противоречие доказывает наше утверждение.