Реальное усилительное звено

Математические модели данного звена имеют вид:

дифференциальное уравнение: ; соответствующая ему передаточная функция: ; частотные характеристики:

- АФЧХ;

- ВЧХ;- МЧХ; причем,.

Следовательно, (АФЧХ) располагается в четвертом квадранте координатной плоскости. Кроме того(выполнили деление). Если подставитьв, то получим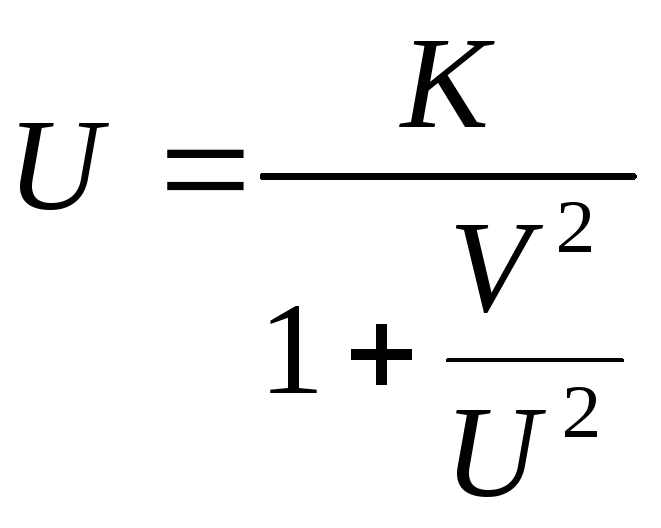, откуда после преобразований:

;;.

Имеем окружность радиусом , сдвинутую навправо по оси абсцисс.

Можно утверждать, что АФЧХ расположена:

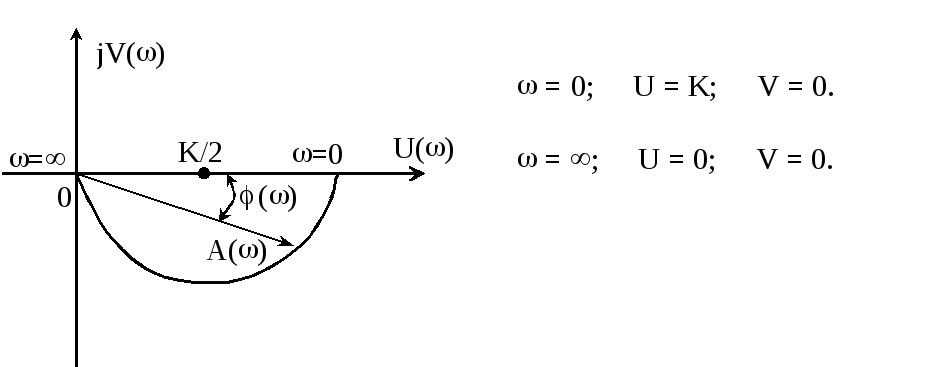
Амплитудно-частотная характеристика реального усилительного звена имеет вид:

Фазово-частотная характеристика: , причем,.

На графиках представлены все полученные зависимости:

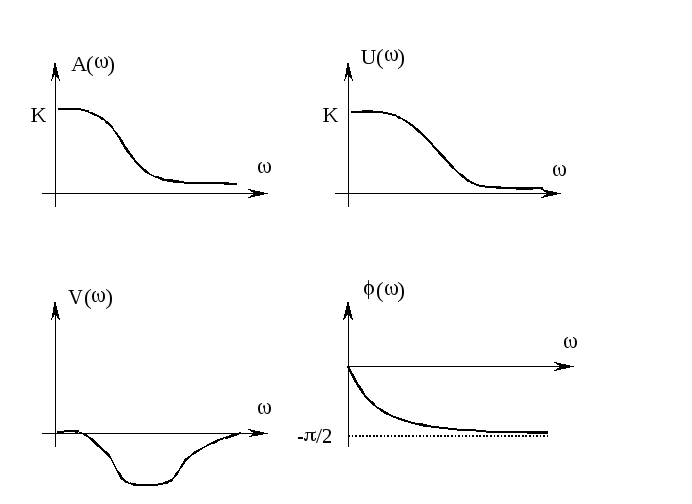
Логарифмическая амплитудно-частотная характеристика (ЛАХ):

.

Для ее построения выполним исследования.

а) Зона низкой частоты. Н.Ч.

,.

б) Зона высокой частоты. В.Ч.

,;;

Наклон характеристики в области высоких частот .

Определим погрешность в точке = 1/T.

.

Это соответствует ошибке по коэффициенту усиления в раз. Но ошибка с изменением частоты быстро уменьшается (смотри на рисунок). Значит, имеет смысл пользоваться асимптотическими характеристиками.

Для определения переходной характеристики звена можно выполнить обратное преобразование Лапласа: ℒ.

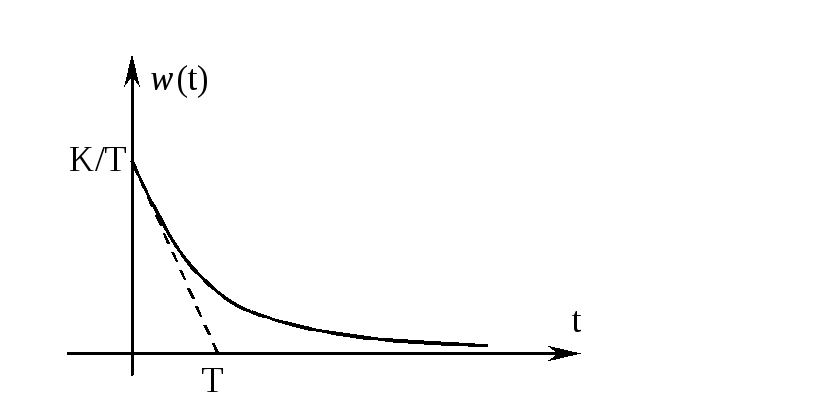
Весовая функция реального усилительного звена: .

По переходной характеристике h(t)можно определить характеристики звена (постоянную времени и коэффициент усиления).

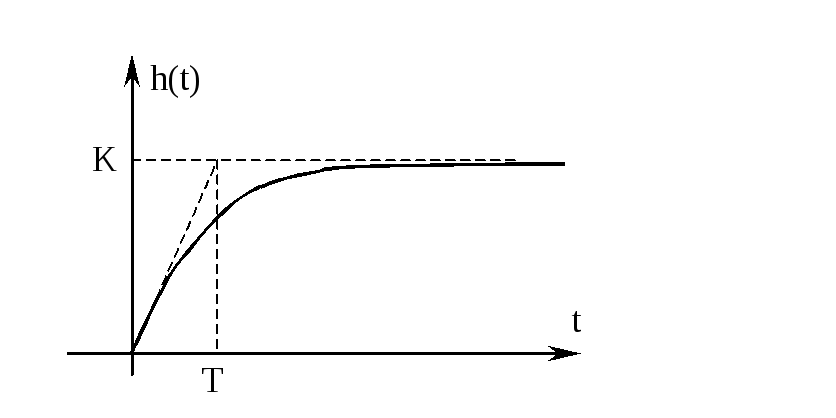
Аналогично те же величины можно определить и из весовой функции звена

Идеальное дифференцирующее звено

Дифференциальное уравнение, передаточная функция и АФЧХ звена имеют вид: ; .

ВЧХ, МЧХ, АЧХ, ФЧХ и ЛАХ звена соответственно равны:

;;;;.

Ниже представлены графики этих зависимостей:

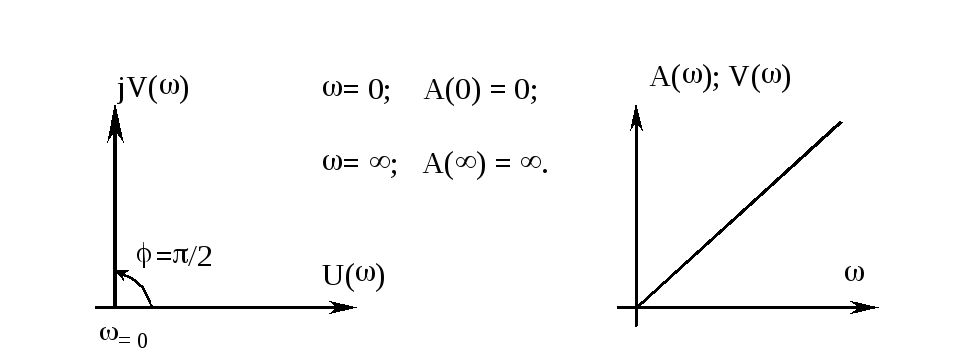
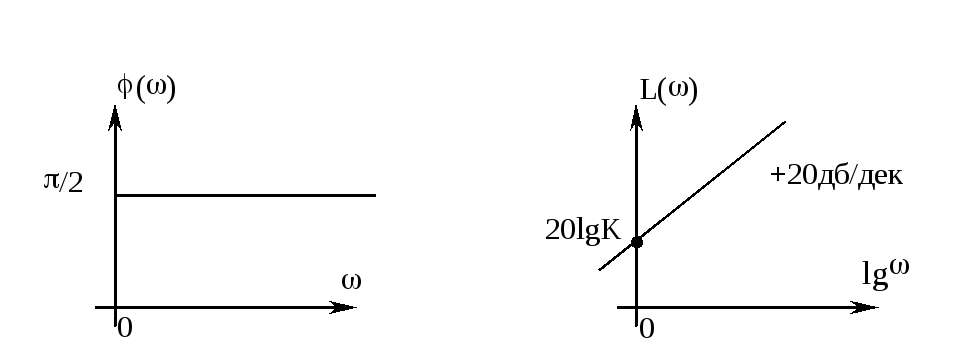
Переходная характеристика и весовая функция звена равны:

ℒℒℒ;.

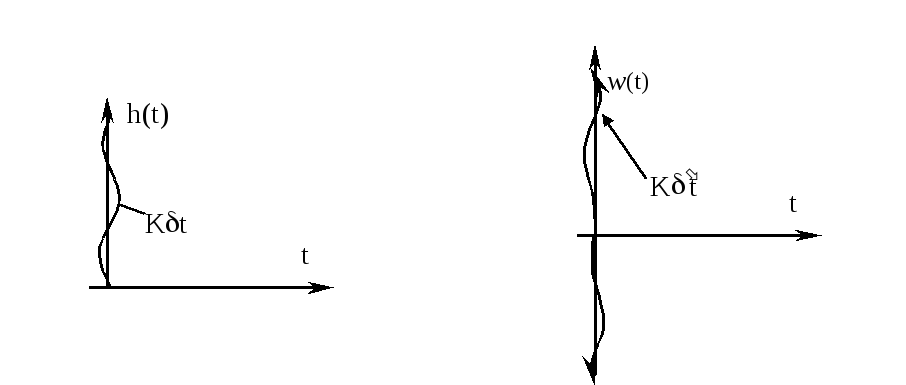
Примеры дифференцирующих звеньев:

1)
2) .			y = Ic ; x = Uc .
3) ;.			y = UL ; x = IL .

Во всех трех случаях имеет место идеальное дифференцирование.

Дифференцирующие звенья - лучшее средство коррекции!

Реальное дифференцирующее звено

Дифференциальное уравнение и передаточная функция такого звена имеют вид: .

Примером реального дифференцирующего звена может служить RC- цепочка:

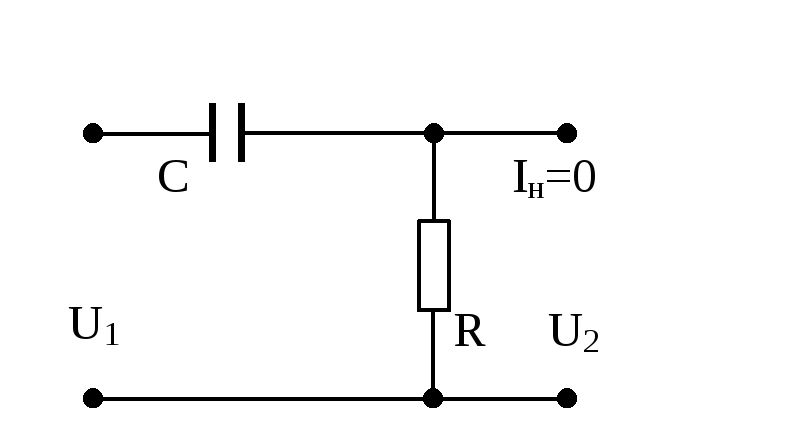
с передаточной функцией .

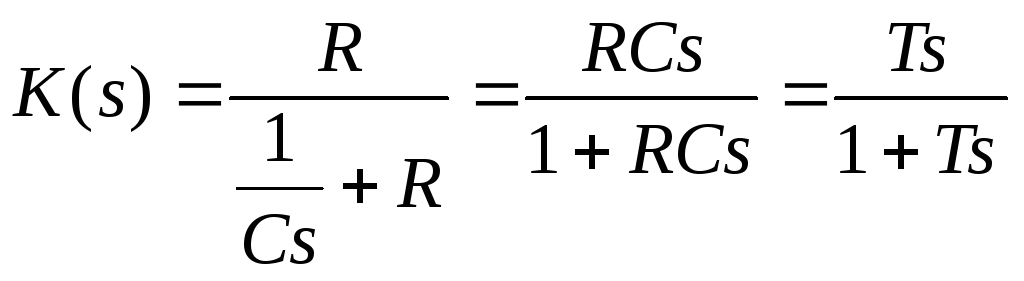Амплитудно-фазовая частотная характеристика реального дифференцирующего звена: ;

ВЧХ и МЧХ:

Причем, при ,. Вся АФЧХ расположится в первом квадранте. Так же, как для апериодического звена, можно показать, что это уравнение окружности.

АЧХ: ; ЛАХ:

Для построения ЛАХ рассматриваются две частотные области - низкочастотная и высокочастотная:

Н.Ч.: ;

В.Ч.: .

ФЧХ:

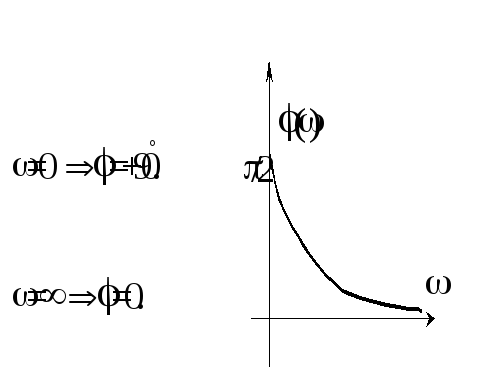
Переходная характеристика:

ℒ;

Весовая функция:.

Это звено также опережающее и его можно применять для коррекции.

Интегрирующее звено

Данному звену соответствует интегральное уравнениеи передаточная функция.

Ниже приведены частотные характеристики интегрирующего звена.

АФЧХ:; ВЧХ:; МЧХ: ; АЧХ:; ФЧХ:;

ЛАХ: .

Построение их не вызывает сложностей. ЛАХ интегрирующего звена изображена на рисунке:

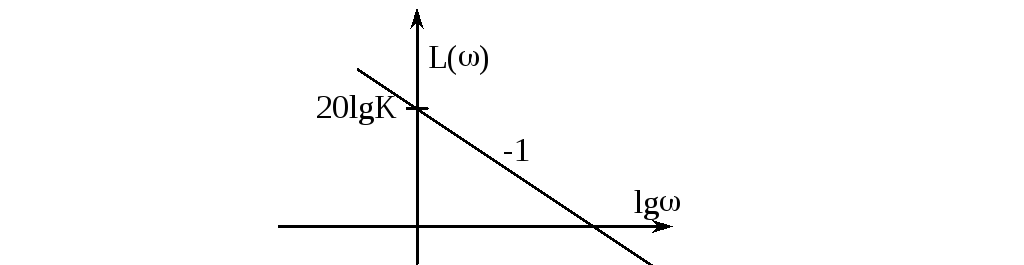
Форсирующеезвено

Данное звено используется в системах автоматического управления для целей коррекции. Его передаточная функция имеет вид:

;

Частотные характеристики:

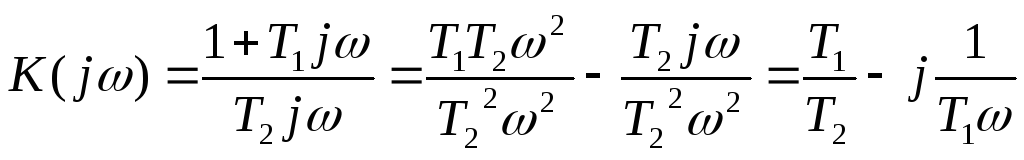АФЧХ: ; ВЧХ:;

МЧХ: ; ФЧХ:;; при.

АЧХ: .

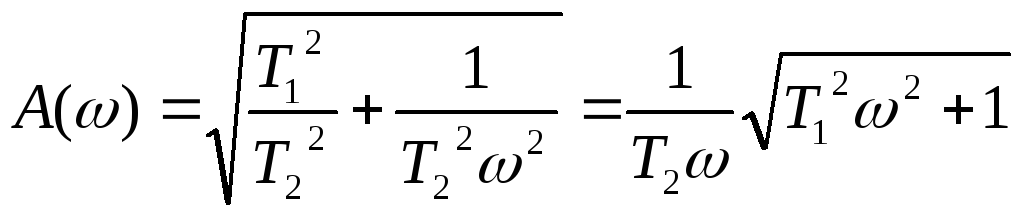ЛАХ: ;

Для построения ЛАХ форсирующего звена рассматриваются области низких частот НЧ и высоких частот ВЧ:

НЧ: ;;

ВЧ: ;.

Точка пересечения ЛАХ оси ординат определяется как:

.