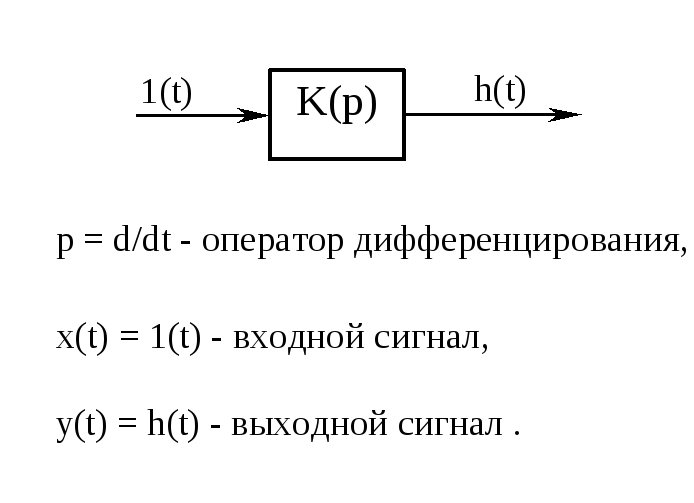
Переходная характеристика звена

Под переходной характеристикой понимается реакция звена на единичное ступенчатое воздействие

-вынужденная составляющая реакции звена;

-свободная составляющая.

; ; =ℒ.

Весовая функция

w(t)- реакция звена на единичный импульс.w(t)ℒ.

Если (t)=1(t), то w(t)=h(t).

Функции h(t)иw(t)могут быть определены, если воспользоваться функцией разложения.

Пусть передаточная функция звена имеет вид: .

Тогда по формуле Хависайде:

, ,

где n–порядок полиномаQ(s),S_k–корни полиномаQ(s)=0.

.

Минимально фазовые и неминимально фазовые звенья

Передаточную функцию звена (элемента системы автоматического управления) можно преобразовать, разложив на множители полиномы ее числителя и знаменателя. Конечно, если известны корни уравнений(нули) и(полюса).

.

Если в передаточной функции произвести замену , то получаем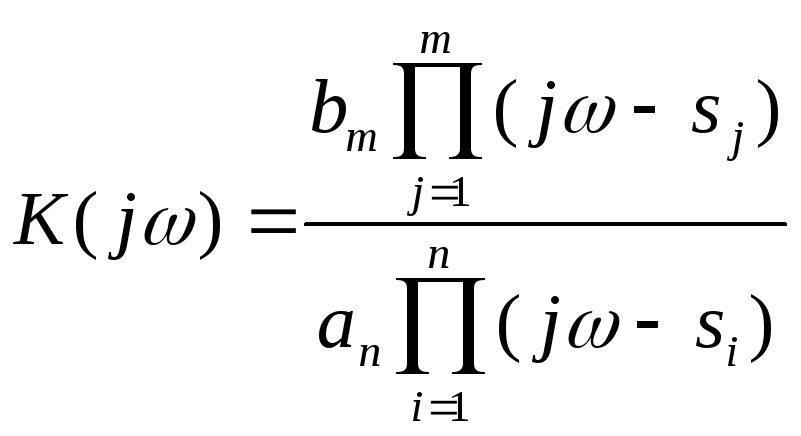, называемое частотной характеристикой звена (частотный коэффициент передачи звена).

Общая фаза выходного сигнала звена будет складываться из частичных фаз, определяемых каждым двучленом числителя и знаменателя. Об этом будет более подробно в соответствующем разделе ниже.

Корни полиномов числителя и знаменателя можно изобразить на плоскости.

Комплексная плоскость корней и :

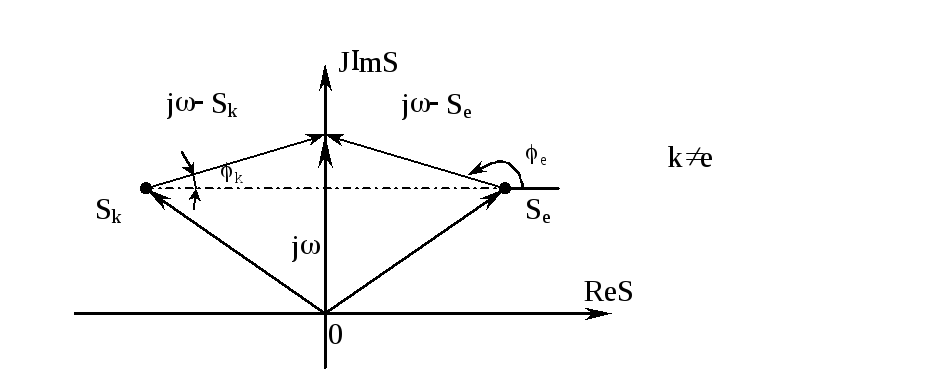
Отсюда:

1. Корень расположен в правой полуплоскости, то естьReS_e0 .

2. Корень расположен в левой полуплоскости, то естьReS_k0.

3. Углы наклона векторов итаковы, что_k_e, причем,.

Звено, у которого все корни (полюса и нули) расположены в левой полуплоскости (являются левыми) называется минимальнофазовымзвеном.

Если хотя бы один из корней звена расположен справа, то такое звено - не минимально фазовое звено.

У минимально фазовых звеньев существует однозначная зависимость между частотными характеристиками.

То есть, располагая одной частотной характеристикой, можно построить остальные. Другими словами, в любой частотной характеристике заключена вся информация о поведении звена.

Неустойчивые звенья - всегда не минимально фазовые.

Типовые звенья. Характеристики звеньев

Все многообразие звеньев может быть по математическому описанию представлено лишь несколькими характерными (типовыми) звеньями.

Минимально фазовыезвенья:

1. Идеальное усилительное звено (пропорциональное безинерционное, усилительное, звено нулевого порядка);

2. Реальное усилительное звено (апериодическое, генерационное первого порядка);

3. Идеальное дифференцирующее звено;

4. Реальное дифференцирующее звено;

5. Идеальное интегральное звено;

6. Идеальное формирующее звено;

7. Звенья второго порядка:

• Апериодическое;

• Колебательное;

• Консервативное.

Не минимально фазовыезвенья:

1. Звено чистого запаздывания;

2. Квазипериодическое звено;

3. Квазиколебательное звено.

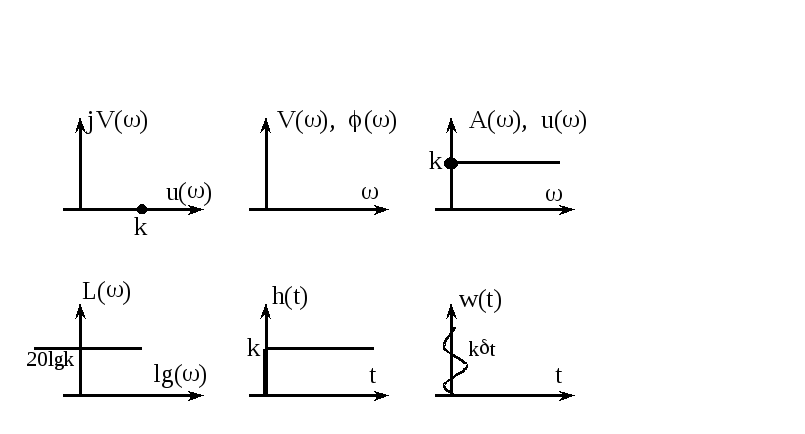
Идеальное усилительное звено

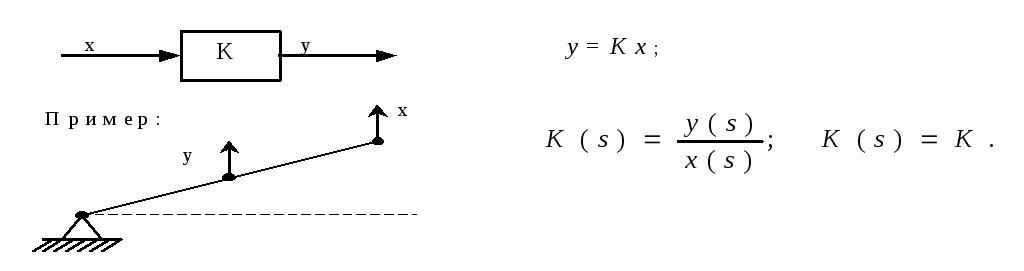
Это рычаг - идеальное звено, если пренебречь весом и потерями в подшипниках.

Получим частотные характеристики идеального усилительного звена. Заменяем в передаточной функции :;

Тогда ВЧХ и МЧХ звена будут определяться как ;;

Фазовая частотная характеристика ФЧХ звена: ;

Амплитудная частотная характеристика АЧХ: ;

Логарифмическая амплитудная характеристика ЛАХ звена: .

Переходная характеристика ℒ.

Весовая функция .

Все характеристики идеального усилительного звена изображены на рисунках: