RGTA

5) Решение системы.

Прежде всего заметим, что система имеет решения: u1 = const, u2 =

ние системы становится тождеством, а второе уравнение принимает

вид: ddt2u22 − u12 ( dudt2 )2 = 0, из которого следует, что u2 = ϕ(t), где ϕ(t)

– решение этого уравнения. Полагая r = ϕ(t), мы получаем уравнения геодезических u1 = const, u2 = r, откуда мы видим, что геодезические линии суть прямые, параллельные оси u2. Проверьте, что ϕ(t) = C2eC1t. Пусть теперь dudt1 6= 0. Тогда существует функция t = t(u1) и мы можем считать u2 = u2(t(u1)) функцией от u1. Найдем формулы, связывающие производные от u2 по t и производные от u2 по u1.

(u2)2 + (u1 − C2)2 = C1.

Таким образом, мы получили, что геодезическим и линиям в заданной метрике являются прямые параллельные оси u2 и окружности

сцентром в любой точке оси u1 и любого радиуса.

6)Параллельное перенесение. Напишем уравнения параллельного переноса вдоль кривой u1 = cos t, u2 = sin t. Пусть λ(t) : (λ1(t), λ2(t)) – поле параллельных векторов вдоль кривой γ с начальными условиями

λ1(π/2) = 0, λ2(π/2) = 1. Тогда

Подставив в выражения для 112, 121, 222, получим

Решение этой системы уравнений дает нам поле векторов параллельных вдоль кривой γ. Но поскольку кривая γ : (u1)2 + (u2) = 1 есть геодезическая линия, то нам достаточно построить поле векторов постоянной длины, образующих с касательными векторами к кривой γ постоянный угол. касательный вектор r к кривой γ в точке γ(t) имеет компоненты – sin t, cos t. Условие ортогональности двух векторов λ(t) и τ(t) в нашем случае запишется таком виде

Функцию α(t) мы найдем из условия: |λ| = |λ0|. Это условие запишется в таком виде.

Основные дифференциальные операторы: gradf, divλ, rotλ и f в римановом пространстве определяются теми же формулами, что и в евклидовом пространстве в криволинейных координатах.

§3 Основная лемма римановой геометрии

Определение 3.3.1. Связность на многообразии M называ-

Заметим, что условие (III.1) равносильно ∂i ∂j = ∂j ∂i или

sij = sji.

Определение 3.3.2. Тензором кручения для произвольных векторных полей называется билинейный функционал T (u, v) = uv −

vu − [u, v]

Упражнение. Проверить, что T (u, v) – тензор. Упражнение. Определить координаты тензора кручения.

Определение 3.3.3. Говорят, что связность совместна с метрикой (M, g), если g = 0, т.е. для любого векторного поля ω ковариантная производная wgij = 0.

Теорема 3.3.1. Следующие условия эквивалентны:

1)wgij = 0 для всех w;

2)dtd hv(t), wti для всех γ(t) C1, что γ˙ v = γ˙ w = 0;

3)dtd hv(t), wti = hγ˙ v, wi + hv, γ˙ wi

Теорема 3.3.2 (Основная лемма римановой геометрии). На каждом римановом многообразии существует, и притом единственная, симметричная связность, согласованная с его метрикой.

Определение 3.3.4. Связность, удовлетворяющая условиям основной леммы римановой геометрии называется связностью ЛевиЧивита.

§4 Риманов тензор кривизны. Различные типы кривизн

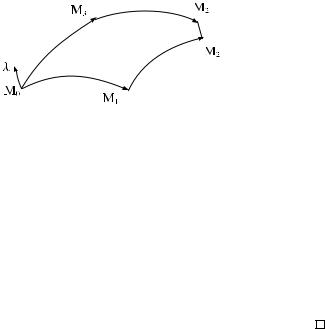
Теорема 3.4.1. Рассмотрим поверхность ui = ui(v1, v2), где функции ui(v1, v2) принадлежат классу C3. Замкнутый контур опреде-

e

лим точками: M0(0, 0), M1(ε, 0), M2(ε, ε), M3(0, ε). Вектор λ есть результат параллельного перенесения вектора λ вдоль контура M0M1M2, вектор λ есть результат параллельного перенесения вектора λ вдоль контура M0M3M2. Тогда

II.Перенесем вектор λ по контуру M0M3M2:

λ= TM0M3 M2 = τ4(τ3(λ)), где τ3(λ) – есть перенос λ по M0M3,

τ4(τ3(λ)) – перенос τ3(λ) по M3M2. Аналогично, получаем

называется римановым тензором кривизны.

Замечание. Если в (III.2) опустить верхний индекс, то получим

Rhkmj = ghiRkmji .

Замечание. Для TM0 M1M2 (λ) и TM0M3 M2 (λ) из теоремы 3.4.1 верно

TM0M1 M2 (λ) − TM0M3 M2 (λ) = ( ∂2 ∂1 − ∂1 ∂2 )λε2 + o(ε2).

Теорема 3.4.2. Значение R(u, v)w в точке x зависит лишь от значений u, v, w в точке x, а не от их значений в близких точках. Отображение R : TxM × TxM × TxM → TxM трилинейно.

Другими словами, теорема утверждает, что Rijkl – тензор, где (R(u, v)w)l = Rijkl uivj wk и Rijkl определяется равенством (III.2).

Теорема 3.4.3. Тензор кривизны риманова многообразия удовлетворяет следующим следующим соотношениям:

1.R(u, v)w + R(v, u)w = 0.

2.Если T = 0, то R(u, v)w + R(v, w)u + R(w, u)v = 0.

3.Если g = 0, то hR(u, v)w, zi + hR(u, v)z, wi = 0.

4.Если T = 0 и g = 0, то hR(u, v)w, zi = hR(w, z)u, vi.

Теорема 3.4.4. Имеет место второе тождество Бианки

gjkRjkli = gjkgisRsjkl = gjkgisRjslk = gisRsl = Rli.

Из второго тождества Бианки с помощью свертки по i и m получаем

Следствие 3.4.3.

Rjkl,ii = Rjk,l − Rjl,k.

Из последних двух следствий вытекает

Следствие 3.4.4.

2Rl,ii = R,l, где R = gjkRjk.

Лемма Шура. Если Kσ(p) = K для любой двумерной площадки σ, то Kσ = K для любой точки p.

называется римановой секционной кривизной в точке p и в двумерном направлении σ, где σ есть плоскость, определенная векторами λ и µ.

Замечание 3.4.1. В двумерном случае формула упрощается

R1212

Kσ = g11g22 − g122

и число Kσ, как можно доказать, совпадает с гауссовой кривизной поверхности в точке p.

Теорема 3.4.5. Если Kσ = 0 для всех точек и для всех двумерных направлений, то риманово пространство является локально евклидовым. Если же для всех точек и для всех двумерных направлений Kσ = +1 (−1), то пространство является локально сферическим (локально изометричным пространству Лобачевского).

Определение 3.4.3. Тензор rij , полученный операцией свертки из риманова тензора кривизны

rij = Rijll ,

называется тензором Риччи.

Определение 3.4.4. Кривизной Риччи Kr(λ) в направлении вектора λ : (λi) в точке p называется число, определенное формулой

Kr = rij λiλj .

Определение 3.4.5. Скалярной кривизной s в точке p называется число, равное s = gij rij .

Упражнение. Доказать, что если в каждой точке поверхности совершено гомотетическое преобразование, т.е. g1 = λg, то выполняются

1)K1 = λ−1K,

2)r1 = λ−1r,

3)s1 = λ−1s.

Пусть {X1, ..., Xn} – базис векторных полей в окрестности U с локальными координатами {xi}. Тогда из разложения по базису имеем

k

Фиксируем базис dxi и рассмотрим 1-форму w = wkdxk на U M и векторные поля X, y X(M). Тогда, в этих обозначениях, справедливы

Лемма 3.5.1.

2dw(X, Y ) = X(wY ) − Y (wX) − w([X, Y ]).

Для дальнейшего изложения совершим замену переменных

X → Xi, Y → Xj

Лемма 3.5.2.

dwi(Xj , Xk) = − 12 cijk.

Лемма 3.5.3.

Tjki = ijk − ikj − cijk.

Доказательство. По определению тензора кручения находим

T (Xj, Xk) = Xj Xk − Xk Xj − [Xj , Xk] = ( ijk − ikj − cijk)Xi.

Сумма полученных равенств дает требуемое.

Упражнение. Проверить, что компоненты тензора кривизны определяются равенствами

§6 Полные римановы многообразия

Пусть M – связное риманово многообразие.

Определение 3.6.1. Параметризованный путь γ : I → M, где I

– некоторый интервал действительной прямой, называется геоде-

зической, если векторное поле ускорения dtD dγdt тождественно равно нулю.

В локальных координатах u1, u2, . . . , un, кривая t → γ(t) M определяет n гладких функций u1(t), u2(t), . . . , un(t), а уравнение геодези-

ческой D dγ dt dt

100 Глава III. РИМАНОВА ГЕОМЕТРИЯ

Таким образом, существование геодезических определяется существованием решений некоторой системы дифференциальных уравнений второго порядка. И согласно известной теоремы теории дифференциальных уравнений для заданных p M, v TpM и t0 R ло-

кально существует геодезическая, удовлетворяющая условиям γ(t0) =

p, dγdt (t0) = v.

Итак, пусть v TpM – касательный вектор, и существует геодезическая

γ : [0, 1] → M,

удовлетворяющая условиям

γ(0) = p, dγdt (0) = v.

Точку γ(1) M обозначим через expp(v) и назовем экспонентой касательного вектора v TpM. Тогда геодезическая γ может быть записана в виде

γ(t) = expp(tv).

Определение 3.6.2. Риманово многообразие M геодезически полно, если экспоненциальное отображение expp(v) определено для всех точек p M и всех векторов v TpM.

Очевидно, что это эквивалентно следующему требованию. Каждый отрезок геодезической γ0 : [a, b] → M продолжается до бесконечной геодезической γ : R → M.

Примерами геодезически полных римановых многообразий слу-

жат: сфера, цилиндр, евклидова плоскость.

Упражнение. Привести пример многообразия, не являющегося геодезически полным.

Определение 3.6.3. Геодезическая γ0 : [a, b] → M называется минимальной, если она не длиннее никакой кусочно-гладкого пути, соединяющего его концы.

Определим расстояние ρ(p, q) между двумя точками p, q M как точную нижнюю грань длин кусочно-гладких дуг, соединяющих эти точки. Очевидно, что при этом M становится метрическим пространством, и эта метрика совместна с обычной топологией на M.

Теорема 3.6.1. (Хопф-Ринов)Пусть M – гладкое полное риманово многообразие. Тогда справедливы следующие утверждения:

1) любые две его точки могут быть соединены минимальной геодезической;