fizika / 1 / mehanika

§22. УРАВНЕНИЕ БЕРНУЛЛИ

Весьма важным уравнением гидроаэромеханики является уравнение Бернулли, определяющее взаимосвязь между давлением и скоростью потока идеальной жидкости (газа). Однако оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых невелико.

Для его вывода рассмотрим стационарное течение идеальной жидкости, т.е. несжимаемой жидкости, в которой отсутствует внутреннее трение, в гравитационном поле. Выделим в жидкости трубку тока и рассмотрим в ней два поперечных сечения S1 и S2. Пусть в этих сечениях скорость жидкости υ1 и υ2, статическое давление P1 и P2, высоты, на которых расположены сечения, h1 и h2, соответственно, (рис. 22.1, на котором показано сечение трубки тока плоскостью чертежа). За

элементарный промежуток времени dt частицы

где W1 и W2 — механическая энергия объёма dV жидкости массой dm в начальном и конечном положениях. Механическая энергия складывается из кинетической и потенциальной энергии тела. Поэтому

поскольку dm = ρ·dV, где ρ — плотность жидкости.

Работу в данном случае совершают лишь силы давления, направленные вдоль траектории движения жидкости, так как силы давления на боковую поверхность трубки тока работы не совершают, вследствие их перпендикулярности к направлению течения жидкости. Она равна dA = dA1 + dA2 = F1 dl1 – F2 dl2, где F1 и F2 — силы, действующие на жидкость в сечениях S1 и S2. Работа dA2 отрицательная, поскольку направления силы и перемещения противоположны (см. (13.1)). Используя определение давления (см. (20.1)), запишем: F1 = P1 S1 и F2 = P2 S2. С учётом этого находим:

60

так как S1 dl1 = S2 dl2 = dV. Подставляя (22.2) — (22.4) в выражение (22.1), после преобразований получаем:

Вследствие произвольного выбора сечений, запишем:

Соотношение (22.6) называется уравнением Бернулли. В нём P — статическое давление, равное давлению, которое оказывает жидкость на поверхность обтекаемого ею тела; ρυ2/ 2 — динамическое давление, т.е. дополнительное давление, которое создаёт жидкость при её остановке; ρgh — гидростатическое давление (см. §20). Это соотношение выполняется тем точнее, чем меньше поперечные сечения трубки тока, т.е. при её стягивании в линию тока.

В качестве примера рассмотрим одно из следствий, вытекающих из уравнения Бернулли. При стационарном течении жидкости по горизонтальной трубке (h1 = h2) из формулы (22.5) следует, что

т.е. статическое давление больше в тех местах, где скорость течения жидкости меньше. Величину P + 12 ρυ2 называют полным давлением. Из уравнения не-

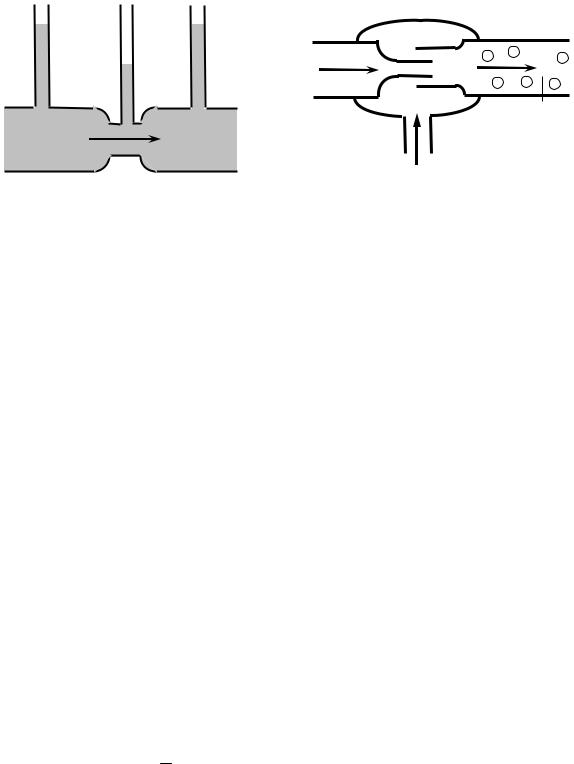
разрывности жидкости (21.3) вытекает, что скорость течения обратно пропорциональна площади поперечного сечения. Поэтому статическое давление уменьшается в местах сужений трубки. В этом можно убедиться, установив вдоль трубки ряд манометров (рис. 22.2). Меньшая высота подъёма жидкости в манометрической трубке, установленной в узкой части трубы, свидетельствует о меньшем статическом давлении в этой части трубы. На этом основано действие

61

водоструйного насоса (рис. 22.3). Давление воды на выходе насоса равно атмосферному давлению. Поэтому в месте сужения давление будет ниже атмосферного и в резервуаре A создаётся разряжение. Трубка B присоединяется к сосуду, из которого надо откачать воздух. Таким способом можно откачать воздух до

давления ≈3 кПа (20 мм рт. ст.).

Для измерения полного давления пользуются трубкой Пито, представляющей собой манометрическую трубку с отверстием, обращённым навстречу потоку (рис. 22.4). Рассмотрим линию тока, упирающуюся в центр отверстия трубки.

Скорость вдоль рассматриваемой линии тока будет изменяться от υ для невозмущённого потока на больших расстояниях от трубки до нуля непосредственно перед отверстием. Используя уравнение Бернулли, находим давление перед от-

§23. ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ

Вязкость (внутреннее трение) — это свойство жидкостей (газов) оказывать сопротивление взаимному перемещению её частей. При движении слоёв жидкости между ними возникают силы трения, названные силами внутреннего трения, направленные по касательной к поверхности слоя. Эти силы тормозят более быстрый слой и ускоряют слой, движущийся медленнее.

Существует два вида течения жидкости — ламинарное и турбулентное. В случае ламинарного течения слои жидкости перемещаются, не перемешиваясь с другими слоями. При турбулентном течении происходит интенсивное вихреобразование и перемешивание различных слоёв жидкости. Рассмотрим ламинар-

62

дящиеся на элементарном расстоянии dz друг от друга, модуль скорости кото-

рых отличается на элементарную величину dυ (рис. 23.1). Отношение ddzυ ха-

рактеризует быстроту изменения скорости различных слоёв жидкости в направлении z, перпендикулярной к слоям. Его называют градиентом скорости. Ньютон установил, что модуль силы внутреннего трения f находится по формуле:

где S — площадь соприкасающихся слоёв, η — коэффициент динамической вязкости, зависящий от природы жидкости (газа). В системе единиц СИ коэффициент динамической вязкости измеряется в Н·с/м2. Коэффициент динамической вязкости зависит от температуры, причём у жидкостей он уменьшается, а у

z

r

Рис. 23.2

газов увеличивается с повышением температуры. Это связано с различием механизмов внутреннего трения в них.

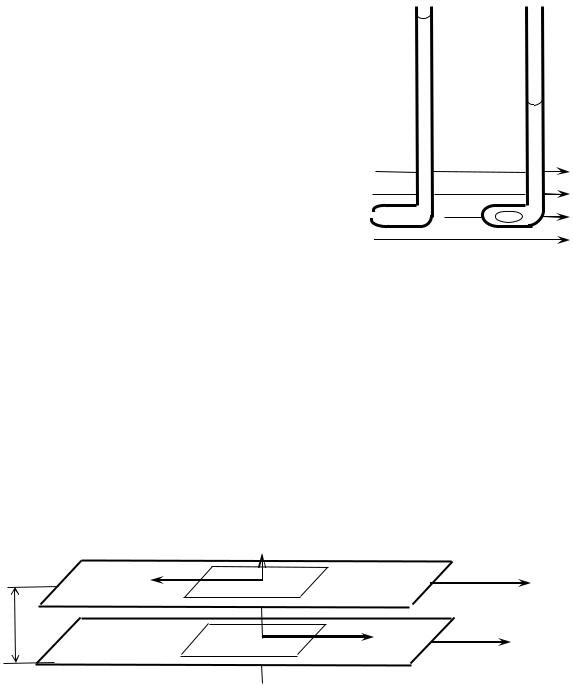
Выясним характер движения жидкости в трубах. При малых скоростях течение будет ламинарным. Слой жидкости, соприкасающийся со стенками трубы, из-за сил молекулярного притяжения будет неподвижным. Скорости последующих слоёв возрастают, достигая наибольшего значения на оси трубы. Распределение скорости ламинарного течения по площади поперечного сечения трубы показано на рис. 23.2 a (приведён продольный разрез трубы плоскостью чертежа). При увеличении скорости протекания жидкости и поперечных размеров трубы, течение становится турбулентным. Скорость слоёв жидкости при турбулентном течении растёт по мере удаления от поверхности трубы, а затем изменяется очень мало (рис. 23.2 б).

Рейнольдс показал, что характер течения жидкости (газа) зависит от безразмерной величины, названной числом Рейнольдса:

где ρ — плотность жидкости (газа), <υ> — средняя по сечению трубы скорость потока, l — характерный для поперечного сечения линейный размер, например,

63

сторона квадрата при квадратном сечении трубы, радиус или диаметр при круглом сечении и т.д. Средняя скорость оценивается по объёму, протекающему через поперечное сечение в 1 с. При малых значениях числа Рейнольдса (Re < 1000) происходит ламинарное течение в цилиндрической трубе, переход от ламинарного течения к турбулентному течению наблюдается в интервале 1000 < Re < 2300, а при Re > 2300 — течение турбулентное. Движения, отличающиеся значениями параметров ρ, η, υ и l, при одинаковом значении числа Рейнольдса имеют одинаковый характер.

§24. ДВИЖЕНИЕ ТЕЛ В ВЯЗКОЙ СРЕДЕ

При движении в вязкой среде (жидкость или газ) тело испытывает сопротивление. Происхождение этого сопротивления двояко. При малых скоростях и удобообтекаемой форме тела, когда не возникает за телом вихрей, сила сопротивления обусловлена вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твёрдому телу, прилипает к его поверхности и полностью увлекается им. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы внутреннего трения. В этом случае модуль силы сопротивления по закону, установленному Стоксом, пропорционален коэффициенту динамической вязкости, скорости и линейным размерам тела, т.е.

где B — безразмерный коэффициент, зависящий от формы тела, υ — скорость тела, l — характерный размер тела. Например, для тел шарообразной формы характерный размер равен его диаметру, а коэффициент — B = 3π.

Другой механизм сопротивления движению тела в вязкой среде связан с образованием за телом вихрей, т.е. позади обтекаемого тела возникает длинная полоса турбулентно движущейся жидкости, называемой турбулентным следом. Схематически этот след показан на рис. 24.1. Скорость жидкости в турбулентном слое больше, чем перед движущимся телом. Поэтому, как это следует из уравнения Бернулли (22.7), давление в турбулентном слое оказывается пониженным. Это и обусловливает появление силы, направленной против движения, т.е. возникает сила сопротивления, которую называют лобовым сопротивлением. Используя теорему о кинетической энергии, найдём зависимость лобового сопротивления от размеров и скорости тела.

Пусть тело со скоростью υ движется в вязкой среде, плотность которой равна ρ. На элементарном пути dl тело оттесняет массу среды, равную dm = ρ dV = ρS dl, где S — площадь поперечного сечения тела, перпендикулярного к направлению

S

υ

64

скорости (рис. 24.2). Изменение кинетической энергии dWк этой массы равно dWк = dm υ2/ 2, так как начальная кинетическая энергия равна нулю. Это изменение кинетической энергии вызывается силой f , действующей наданнуюмассу среды со стороны тела. Элементарная работа dA, совершённая этой силой, находится по формуле dA = f dl, поскольку направление силы совпадает с направлением перемещения. Согласно теореме о кинетической энергии, запишем dA = dWк. Подставляя в это равенство выражения для dWк и dA, получаем f dl = dm υ2/ 2 = ρ S dl υ2/ 2. Отсюда f = ρυ2S/2. По третьему закону Ньютона такая же сила fс действует на тело со стороны среды, т.е. fс = ρυ2S/2. Более точные расчёты показывают, что лобовое сопротивление находится по формуле:

где Cх — безразмерный коэффициент, зависящий от формы тела. Он уменьшается с улучшением аэродинамических свойств тела, когда за ним остаётся меньшее количество завихрений. Из формулы (24.2) следует, что лобовое сопротивление возрастает с увеличением скорости быстрее, чем сила внутреннего трения (см. (24.1)), а также увеличивается с увеличением плотности среды и площади поперечного сечения тела.

При движении тела на него действуют как сила внутреннего трения, так и лобовое сопротивление. Для определения вклада каждой из этих сил поделим выражения (24.2) и (24.1) друг на друга:

поскольку S ~ l2. Выражение υ2 nr можно рассматривать как число Рейнольдса.

R

Только под υ и l надо понимать скорость и характерный размер тела. Из (24.3) следует, что при Re « 1 сопротивление обусловливается силами внутреннего трения, а лобовое сопротивление можно не учитывать, и, наоборот, при Re » 1 не надо принимать во внимание силы внутреннего трения.

ОСНОВНЫЕ ВЫВОДЫ

1. Давлением называется сила, приходящаяся на единицу площади площадки, перпендикулярной к ней, при условии её равномерного распределения:

A=1k(r−r)2−1k(r−r)2 где dF — модуль силы, приходящейся на площадку dS. p21 н 22 н

2. Закон Паскаля: давление, производимое на покоящуюся жидкость (или газ), передаётся по всем направлениям одинаково.

65

3.Уравнение неразрывности жидкости (газа) имеет вид ρυS = const. Здесь

ρи υ — плотность и скорость жидкости в любом сечении S трубки тока. Это уравнение является следствием закона сохранения массы. В случае несжимае-

мой жидкости (ρ = const) уравнение записывается υS = const.

4. Уравнение Бернулли представляет собой выражение закона сохранения энергии для стационарного течения невязких жидкостей: P + 12 ρυ2 + ρgh = const ,

где P, ρυ2/ 2 и ρgh — статическое, динамическое и гидростатическое давления жидкости, соответственно.

5. Вязкость (внутреннее трение) — свойство жидкостей (газов) оказывать сопротивление взаимному перемещению её частей. Существуют два вида течения жидкости (газа) — ламинарное и турбулентное. Характер течения определяется

числом Рейнольдса: Re = ρ υη l . Здесь ρ — плотность жидкости (газа), <υ> —

средняя по сечению трубы скорость потока, l — характерный для поперечного сечения линейный размер.

При движении тела в вязкой жидкости число Рейнольдса пропорционально отношению модуля лобового сопротивления к модулю силы внутреннего трения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Дайте понятие давления.

2.Сформулируйте закон Паскаля.

3.Какое давление называют гидростатическим?

4.Сформулируйте закон Архимеда.

5.Выведитеуравнениенеразрывностижидкости. Вчёмсмыслэтогоуравнения?

6.Выведите уравнение Бернулли. Какой смысл этого уравнения?

7.Каковы следствия из уравнения Бернулли?

8.Что называется вязкостью (внутренним трением)?

9.Какие виды течения жидкости (газа) существуют?

10.Запишите закон Ньютона для ламинарного течения жидкости.

11.Что такое число Рейнольдса и что оно характеризует?

12.Запишите закон Стокса.

13.Что такое лобовое сопротивление? Какова его природа?

ЗАДАЧИ

5.1.Какова сила давления на боковую поверхность цилиндрического резервуара радиусом 2 м и высотой 5 м, заполненного бензином? Плотность бензина 700 кг/м3.

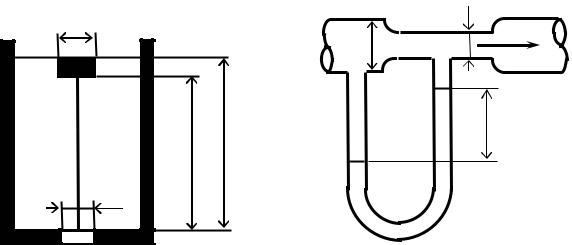
5.2.Определить массу поплавка диаметром D = 0,2 м (рис. 5.1), который бы при слое бензина H = 0,8 м обеспечивал автоматическое открывание клапана диаметром d = 0,04 м. Массу

клапана с тягой принять равной m = 0,17 кг. Длина тяги — h = 0,74 м, плотность бензина — ρ= 700 кг/м3. Толщинойклапанапренебречь.

66

5.3.По напорному трубопроводу перекачивается загрязнённая жидкость. Известно, что осаждение загрязнений в трубопроводе будет исключено, если жидкость движется со

скоростью не менее 1,5 м/с. Найти максимально допустимый диаметр трубопровода, при котором не будет происходить отложений взвеси, если расход 0,03 м3/с.

5.4.Определите расход нефти (объём нефти, протекающий в 1 с) по трубопроводу, имею-

щему сужение, если d1 = 15 см, d2 = 10 см, и разность уровней в ртутном дифференциальном пьезодатчике h = 15 мм. Плотность ртути — ρ = 13600 кг/м3 (рис. 5.2). Плотность нефти — 850 кг/м3.

5.5.Какое давление создаёт компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью 20 м/с. Плотность краски — 800 кг/м3.

5.6.Какой наибольшей скорости может достичь дождевая капля диаметром 0,3 мм и железный

шар диаметром 10 см? Плотность воздуха 1,3 кг/м3, его динамическая вязкость 1,2 10-5 Н с/м, плотность железа 7800 кг/м3. Коэффициент Сх принять равным 0,5.

5.7.Найти скорость течения углекислого газа по трубе, если известно, что за время 30 мин через поперечное сечение трубы протекает 0,5 кг газа. Плотность газа — 7,5 кг/м3. Диаметр трубы 2 см.

5.8.Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом.

Найти динамическую вязкость касторового масла, если шарик всплывает с постоянной скоростью 3,5 м/с. Плотность пробки 200 кг/м3, а масла — 900 кг/м3.

5.9.Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения, действующая на всплывающий шарик, больше силы тяжести шарика.

5.10.Вода течёт по трубе, причём за единицу времени через поперечное сечение трубы протекает объём воды 200 см3/с. Динамическая вязкость воды 0,001 Па с. При каком предельном значении диаметра трубы движение воды остаётся ламинарным? Ламинарность движения воды сохраняется при числе Рейнольдса Re ≤ 2000 (если при вычисле-

нии Re в качестве характерного размера принять диаметр трубы). Плотность воды —

1000 кг/м3.

67

ГЛАВА 6. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ

До сих пор рассматривались вопросы классической механики, изучающей движение со скоростями, много меньшими скорости света, c = 300000 км/с. В обыденной жизни мы имеем дело только с такими скоростями. Даже самые высокие из них, которые встречаются в космических полётах (8 — 12 км/с), хорошо удовлетворяют условию υ « c. Однако при рассмотрении движений микрочастиц (например, электронов, протонов в сильных электрических и магнитных полях) физики сталкиваются со скоростями, близкими к скорости света. Оказалось, что законы классической физики в этом случае либо применимы ограниченно, либо не применимы совсем. Все это привело к разработке теории движения тел при скоростях, соизмеримых со скоростью света, которая получила название релятивистская механика. В её основе лежит специальная теория относительности, созданная в начале двадцатого века Эйнштейном. В данной главе рассматриваются основные понятия и элементы этой теории. Прежде чем приступить к изложению этих нетривиальных вопросов, необходимо понять принцип относительности Галилея, имеющий к этому непосредственное отношение.

§25. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ

Любое механическое движение является относительным. Поэтому о движении тела можно говорить, лишь указав систему отсчёта. Известно, что законы механики выполняются только в инерциальных системах отсчёта и при этом сохраняется их форма записи. Это положение называют принципом относи-

тельности Галилея: во всех инерциальных системах отсчёта механические процессы протекают одинаково. Галилей поясняет этот принцип на таком примере. "Заключите себя с каким-нибудь приятелем в зале под палубой како- го-нибудь большого корабля ... и заставьте привести в движение корабль с какой угодно быстротой. И вот (если только движение прямолинейное и равномерное) вы не заметите ни малейшей перемены во всех явлениях и ни по одному из них не в состоянии будете судить — движется ли корабль или стоит на месте: вы, прыгая, будете проходить по полу те же пространства, как и при покое корабля, т.е. вы не сделаете — от того, что корабль движется — бульших прыжков к корме, чем к носу, хотя в то время, когда вы находитесь в воздухе, пол, находящийся под вами, бежит в сторону, противоположную вашему прыжку ...". С точки же зрения наблюдателя, находящегося на берегу, движение корабля будет прямолинейным и равномерным, а длина прыжков в направлении движения будет больше, чем в противоположном. В этом и проявляется относительность движения.

В связи с относительностью движения часто возникает необходимость перехода из одной инерциальной системы отсчёта в другую. В классической механике такой переход осуществляется с помощью преобразований Галилея. Эти

68

преобразования связывают между собой координаты какой-либо материальной точки в двух различных инерциальных системах отсчёта, когда скорости движения много меньше скорости света.

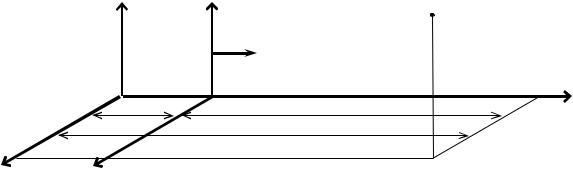
Пусть относительно инерциальной системы отсчёта K движется со скоростью υ другая система отсчёта K′. Для упрощения рассуждений предположим, что направления координатных осей Ox и O′x′ совпадают (рис. 25.1). Обозначим координаты точки M в системе отсчёта K в произвольный момент времени t через x, y, z, а координаты той же точки в системе отсчёта K′ — через x′, y′, z′ в тот же момент времени t′. В классической механике считается, что время в любой инерциальной системе отсчёта течёт одинаково, т.е. t = t′. Простым примером является движение человека в вагоне поезда, идущего с постоянной скоростью υ: K система отсчёта, связанная с Землей, K′ с поездом, точка M указывает положение человека. Допустим, что в момент времени t = t′ = 0 начала координат совпадали, т.е. x = x′ = 0. Тогда, как видно из рис. 25.1, в момент времени t координаты материальной точки y = y′ и z = z′, а абциссы отличаются на отрезок OO′ = υt. Отсюда преобразования Галилея при переходе от одной системы отсчёта к другой принимают вид:

Видно, что преобразования Галилея удовлетворяют принципу относительности, так как они получаются один из другого заменой υ на −υ, поскольку скорость системы K относительно K′равна −υ

§26. СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ГАЛИЛЕЯ

Из преобразований Галилея вытекает ряд следствий.

1. Классический закон сложения скоростей. Пусть точка М движется с не-

которой скоростью u′ относительно системы К′. Какова скорость этой точки в системе К? Для ответа на этот вопрос продифференцируем уравнения (25.2) по

69