

ства, наконец, между кривыми плавления и испарения — жидкому состоянию. Как уже указывалось, любая точка, лежащая на одной из указанных кривых, изображает равновесное состояние двух соответствующих фаз вещества. Таким образом, каждая точка на диаграмме давление — температура соответствует определённому равновесному состоянию вещества. Поэтому её называют диаграммой состояния. На рис.67.1 приведена диаграмма состояния для веществ, у которых плотность в твёрдом состоянии больше, чем в жидком. У них с повышением давления температура плавления возрастает. Однако у некоторых веществ, наоборот, плотность вещества в твёрдом состоянии меньше, чем в жидком. Для них с повышением давления температура плавления понижается (см. §65, пункты 2 и 3). Диаграмма состояния для этих веществ показана на рис. 67.2. Для вещества с несколькими кристаллическими фазами диаграмма состояния имеет более сложный характер. На рис. 67.3 изображена диаграмма для случая, когда у вещества две твёрдых кристаллических фазы. У таких веществ две тройных точки. В точке D в равновесии находятся первая кристаллическая фаза, жидкость и газ, а в точке D1 — жидкость и обе твёрдые фазы.
Диаграмма состояния для каждого вещества строится на основе опытных данных. Зная её, можно предсказать состояние вещества при различных условиях (при разных давлениях и температурах), а также превращения вещества при различных процессах. Поясним это на примерах. Возьмём вещество в состоянии, соответствующем точке a на рис. 67.3, и подвергнем его изобарическому нагреванию, то на участке a – a' происходит повышение температуры кристалла до температуры плавления, в состоянии a' наблюдается плавление кристалла и превращение его в жидкость. В этом состоянии одновременно существуют твёрдая и жидкая фаза вещества. Когда кристалл полностью расплавится, то температура жидкости начинает повышаться (участок a' – b') до температуры кипения. В состоянии b' жидкость кипит при постоянном давлении. После того, как она полностью выкипит, образуется ненасыщенный пар (газ), температура которого вновь повышается (участок b' – b). Если же вещество
подвергнуть |
изобарическому |
нагреванию |
при |
P |
|
|
|
давлениях, |
меньших давления |
тройной |
точки |
|
|
||
(прямая линия c–c'–d), то кристаллы превраща- |
|
К2 |
|
||||
ются в газ, минуя жидкое состояние. |
|
|
|
|
|||
Из диаграмм (рис. 67.1 — 67.3) видно, что |
|
|
|
||||
жидкая фаза может существовать в равновесном |
К1 |
|
|
||||
состоянии лишь при давлениях не меньших дав- |
|
Ж |
|||||
D1 |
|
||||||
ления тройной точки. Поэтому переход большин- |
|
|
|||||
ства веществ из твёрдого состояния в газ осуще- |
a |
a′′ |
b′′ b |
||||
ствляется через жидкую промежуточную фазу, |
|
|
|
||||
так как у них давление в тройной точке значи- |
c |
c′′ D |
Г |
||||
тельно ниже атмосферного. Так, например, трой- |
d |
||||||
ной точке воды соответствует давление ~ 609 Па. |
|
|
T |
||||
Для углекислого |
газа (СО2) давление тройной |
Рис. 67.3 |
|
||||
точки, примерно, |
равно 500 кПа (атмосферное |
|
|||||
|
|
|
|||||
168
давление, примерно, 100 кПа). В силу этого, при атмосферном давлении вещество может существовать только в твёрдом (сухой лёд) и газообразном состояниях. Сухой лёд непосредственно превращается в газ.
ОСНОВНЫЕ ВЫВОДЫ
1.Фазой называют часть термодинамической системы, обладающей одинаковыми физическими свойствами. Это понятие в какой-то мере ассоциируется с понятием агрегатного состояния вещества, но оно, однако, шире. Так, например, различные кристаллические модификации (разновидности) вещества также представляют собой различные фазы.
2.При определённых условиях разные фазы одного и того же вещества, находясь в соприкосновении, остаются в равновесии друг с другом, т.е. их массы не меняются. Равновесие двух фаз наблюдается только при определённых значениях параметров состояния. Поэтому состояние равновесия двух фаз, например, на диаграмме (координатной плоскости) давление P — температура T изображается точкой, асовокупностьтакихсостояний— линией, т.е. графикомзависимостиP = f (T).
3.Процессы, в результате которых происходит превращение одной фазы ве-
щества в другую, называются фазовыми превращениями или фазовыми пере-
ходами. Переходы вещества, связанные с изменением расположения его атомов или молекул, называют фазовыми превращениями первого рода. Эти превра-
щения сопровождаются поглощением или выделением определённого количества теплоты. При фазовых переходах второго рода не происходит выделения или поглощения количества теплоты, а наблюдается лишь скачкообразное изменение некоторых физических свойств вещества.
4.Парообразованием называется процесс перехода вещества из жидкого состояния в газообразное, а обратный процесс называют конденсацией. Испарение — это процесс парообразования, происходящий с открытой поверхности жидкости при любой температуре.
5.Состояние термодинамической системы, при котором число молекул, покидающих жидкость, равно числу молекул, возвращающихся в неё, называют динамическим равновесием, а пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным. Насыщенный пар при данной температуре имеет определённую плотность, называемую равновесной. Это обусловливает неизменность равновесной плотности, а следовательно, и давления насыщенного пара от его объёма, поскольку уменьшение или увеличение объёма этого пара приводит к конденсации пара или к испарению жидкости, соответственно.
6.Кипение — это процесс парообразования, происходящий по всему объёму жидкости при постоянной температуре, называемой температурой кипения, которая зависит от природы жидкости. Кипение в жидкости возникает лишь в тот момент, когда давление насыщенного пара жидкости в газовых пузырьках, находящихся в ней, становится равным внешнему давлению. Температура, соответствующая этому давлению насыщенных паров, и является температурой ки-
169
пения жидкости. С изменением внешнего давления, кипение происходит при различных давлениях насыщенного пара жидкости в газовых пузырьках, а следовательно, и при разных температурах.
7.Плавлением называют процесс перехода вещества из твёрдого состояния в жидкое. Существует два вида твёрдых тел — кристаллические и аморфные. Плавление кристаллических тел происходит при определённой для каждого вещества температуре, называемой температурой плавления, и требует затраты некоторого количества теплоты, называемого теплотой плавления. При плавлении аморфных тел нет определённой температуры перехода в жидкость. Можно лишь указать интервал температур, при котором происходит размягчение тела. Процесс перехода вещества из жидкого состояния в твёрдое называется отвердеванием. В случае кристаллических тел его называют кристаллизацией.
8.Процесс перехода вещества из твёрдого состояния в газообразное называет-
ся сублимацией, или возгонкой.
9.Если в одной координатной плоскости, например, P — T, изобразить кривые равновесия двух фаз жидкость — насыщенный пар (кривая испарения), жидкость — кристалл (кривая плавления) и кристалл — насыщенный пар (кривая сублимации) какого-нибудь вещества, то они пересекаются в одной точке, называемой тройной точкой. В этом состоянии вещество одновременно находится в трёх равновесных состояниях — твёрдом, жидком и газообразном. При этом кривые испарения, плавления и сублимации делят координатную плоскость на три области. Ниже кривых сублимации и испарения находятся точки, соответствующие газообразному состоянию вещества, слева от кривых сублимации и плавления точки соответствуют кристаллическому (твёрдому) состоянию, между кривыми плавления и испарения — жидкому состоянию (см. рис. 67.1 и 67.2). Каждая точка на диаграмме давление — температура соответствует определённому равновесному состоянию вещества. Поэтому её называют диаграммой состояния. Знание диаграмм состояния вещества позволяет предсказывать, в каком состоянии будет находиться вещество при определённых значениях давления и температуры.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называют фазой вещества и фазовыми переходами?
2.Что называется испарением, конденсацией, кипением, плавлением, отвердеванием и сублимацией?
3.Какой пар называется насыщенным?
4.Что называют тройной точкой?
5.Что такое диаграмма состояния и для чего она нужна?
170
Приложение 1
ДЕЙСТВИЯ НАД ВЕКТОРАМИ
Существуют три вида векторов: свободные, т.е. векторы, которые могут быть отложены из любой точки пространства; скользящие, начало которых может перемещаться вдоль прямой, проведённой через вектор; связанные, т.е. векторы, приложенные к определённой точке. Скользящие и связанные векторы могут быть
r |
а) |
r |
|
б) |
b |
в) |
a |
|
c |
|
a |
|
|
|
|
a |
|
|
||
|
b |
|
|
|
cr |
|
b
Рис. П. 1.1
выражены через свободные векторы. В силу этого, векторное исчисление основываетсянапонятиисвободноговектора, обычноназываемого простовектором.
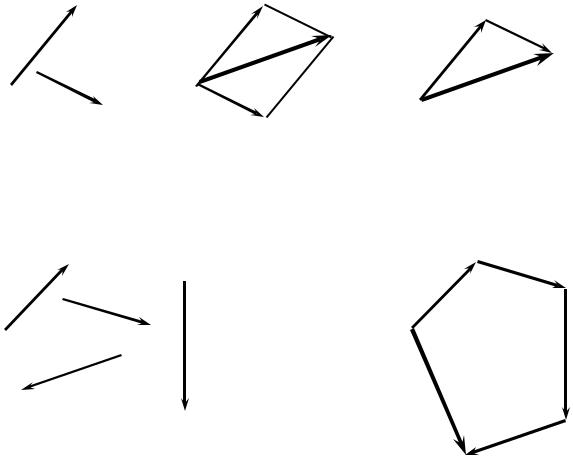
1. Сложение векторов. Пусть имеется два вектора a и b |
рис. П. 1.1, а). Для |
||||
нахождения вектора cr, равного сумме |
этих векторов, т.е. |
вектора cr |
= ar + b, |
||
перенесёмr вектор br |
(или ar) так, чтобы начала векторов совпали. Затем построим |
||||
a1 |
r |
а) |
r |
ar2 |
б) |
|
a2 |
|
a |
|
|
|
|
ar3 |
1 |
|
|
|
|
|
r |
||
|
|
|
|
a3 |
|
|
ar4 |
|
a |
|
|
ar4
Рис. П. 1.2
несём вектор b (или ar) так, чтобы начала векторов совпали. Затем построим на них параллелограмм. Диагональ этого параллелограмма и есть векторrc (рис.
П.1.1,б). Вектор cr можно найти и иным способом. Перенесём вектор b параллельно самому себе таким образом, чтобы его начало оказалось совмещённым с концом вектора arr (рис. П. 1.1, в). Тогда вектор, проведённый из начала вектора a
в конец вектора b , и будет вектором cr = ar + b. Последний способ особенно удобен при сложении нескольких векторов.
Пусть даны, например, четыре вектора a1, a2 , a3 и a4 (рис. П. 1.2, а). Перене-
сём векторы параллельно самим себе так, чтобы начало последующего вектора совпало с концом предыдущего в любой последовательности (рис. П. 1.2, б). Получается ломаная линия. Соединив начало первого отложенного вектора с концом по-
171

следнего, получим вектор ar, равный a = a1 + a2 + a3 + a4 . Этот способ сложения векторов называют методом многоугольника.
ar |
2. Вычитание векторов. Разностью двух векторов a |
|
и b называют такой вектор c , который в сумме с векто- |
||
|
||
r |
ром b даёт вектор a . Поэтому для нахождения вектора |
|
br c |
cr,rравного cr = ar − b, надо соединить концы векторов a |
|
|
и b и провести вектор c в сторону уменьшаемого, т.е. в |
|
|
|
сторону вектора a (рис. П. 1.3). |
|
Рис. П. 1.3 |
3. Умножение и деление вектора на скаляр. В ре- |
||
зультате умножения вектора a на скаляр n получается |
|||
новый вектор cr |
|
||
, модуль c которого равен c = |n| a, а направление его совпадает с |
|||
вектором ar, если скаляр n положительный, и противоположно вектору ar, когда
скаляр n отрицательный. Деление вектора a на скаляр m равносильно умножению этого вектора на скаляр n = 1/m.
4r. Векторное произведение векторов. Векторным произведением векторов a
и b называется вектор cr, перпендикулярный к этим векторам и направленный так, что после совмещения начал указанных векторов кратчайший поворот от a к
b казался бы наблюдателю, смотрящему с конца вектора c , идущим против часовой стрелки (рис. П. 1.4). Модуль c этого вектора равен c
= ab sinα, где α — угол между векторами a и b , приведён- |
|
cr |
|
|||
ными к общему началу. Из рис. П. 1.4 видно, что модуль c |
|
|
b |
|||
равен площади параллелограмма, построенного на векторах |
|
|
||||
|
|
|
||||
r |
r |
r |
|
|
α |
r |
a |
и b , а вектор c перпендикулярен к плоскости этого па- |
|
||||
раллелограмма. Векторное произведение векторов a и b |
|
|
a |
|||
обозначается как [ ar b ] или ar × b . |
|
Рис. П. 1.4 |
||||
|
5. Скалярное произведение векторов. Скалярным произ- |
|
|
|
||
|
|
r |
r |
|
|
|
ведением векторов a |
и b (обозначается a b ) называется скаляр, определяемый ра- |
|||||
|
r |
r |
|
r |
, приведёнными к |
|
венством a |
b = ab cosα, где α — угол между векторами a и |
b |
||||
общемуначалу.
Приложение 2
ПРОИЗВОДНАЯ
1. Производной, обозначаемой через y′, некоторой функции y = f (x) по аргументу x называется предел отношения приращения функции y = f (x + x) – f (x) к приращению аргумента x при его стремлении к нулю, т.е.
y′ = lim |
y . |
(П.2.1) |
x→0 |
x |
|
172

Дифференциалом dy той же функции называют выражение dy = y′dx, где dx — дифференциал аргумента, равный бесконечно малому приращению аргумента. Отсюда
y′ = |
dy |
, |
(П.2.2) |
dx |
т.е. производная— этоотношениедифференциалафункциикдифференциалуаргумента.
В действительности же предельный переход, указанный в формуле (П.2.1), по ряду причин (например, в силу атомистического строения вещества, погрешностей измерений и т.д.) осуществить невозможно. Это идеализированная абстракция, идеализированное представление. Поэтому в физике поступают иначе. Предположим, что необходимо измерить скорость снаряда, движущегося в воздухе в некоторой точке М траектории (рис. П.2.1). Для этого надо измерить расстояние l, в котором находится данная точка, и промежуток времени t, за который сна-
|
ряд пролетает это расстояние, и взять отношение |
l . |
||
М |
|
|
t |
|
Уменьшая |
t, а следовательно, и l, можно заметить, что |
|||
l |
||||
отношение |
l при этом изменяется. Однако, начиная с |
|||
|
|
t |
|
|
Рис. П. 2.1 |
какого-то значения t и l, отношение этих величин ос- |
|||
|
таётся постоянным в пределах доступной точности из- |
|||
мерения. Обозначим эти значения, соответственно, через dt и dl. Назовём их элементарными. С учётом этого, модуль υ скорости равен:
υ = dl . |
(П.2.3) |
dt |
|
С элементарными величинами физики обращаются как с дифференциалами. Поэтому можно сказать, что скорость — это производная пути по времени. Таким об-
разом, в физике производная равна отношению конечных достаточно малых (элементарных) приращенийфункциииаргумента, анекакпределэтогоотношения.
2. Частная производная функции нескольких переменных u = f (x,y,z,t) по одной из них, например по x, обозначаемой ∂∂ux , определяется равенством
∂u |
= lim |
f (x + |
x, y, z,t) − f (x, y, z,t) |
. В этом случае приращение получает |
∂x |
|
x |
||
x→0 |
|
|||
лишь одна из независимых переменных. Функция n переменных имеет n част-
ных производных первого порядка: ∂∂ux , ∂∂uy , ∂∂uz , ∂∂ut и т.д. Частная производ-
ная находится по правилам дифференцирования функции одной переменной, причём остальные переменные рассматриваются в данном случае как постоянные.
3. Правила дифференцирования, т.е. нахождения производной функции одной переменной.
173

а) Производная алгебраической суммы двух или нескольких функций равна алгебраической сумме производных от каждой функции: dxd (u +υ − w +K)= dudx + ddxυ − dwdx +K
б) Производная произведения двух или нескольких функций равна: для двух функций (uυ)′ = u′υ + uυ′; для трёх функций (uυw)′= u′υw + uυ′ w + uυw′.
в) Из правила б) следует (Cu)′ = Cu′ , т.е. постоянную величину можно выносить за знак производной или, наоборот, вносить.
г) Производная от дроби находится по формуле |
u ′ |
υu′ − uυ′ |
. |
υ = |
υ2 |
д) Производная функции от функции (сложной функции) вычисляется по
формуле: |
|
du |
|
= |
du |
|
dυ |
K |
dy |
, если u = f (υ), υ = f (z), ... , y = f (x). |
|||||||||||||||
|
dx |
dυ |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dz |
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4. Таблица производных некоторых элементарных функций |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Функция |
|
|
Произ- |
|
Функция |
Произ- |
|
Функция |
Производ- |
|||||||||||||||
|
|
|
|
|
|
|
водная |
|
|
|
водная |
|
|
|
tg x |
|
|
|
ная |
|
|||||
|
С (постоянная |
) |
0 |
|
|
|
ln x |
1/x |
|
|
|
|
1/cos2x |
|
|||||||||||
|
xn |
|
|
|
|
|
nxn–1 |
|
|
sin x |
cos x |
|
|
|
ctg x |
|
–1/sin2x |
|
|||||||
|
ex |
|
|
|
|
|
|
ex |
|
|
cos x |
–sin x |
|
|
|
|
|
|
|
|
|
|
|||
|
5. Производные высших порядков. Если производная |
dy |
также является |
||||||||||||||||||||||
|
dx |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d dy |
||||||
функцией от x, то от неё можно снова найти производную, т.е. |
|||||||||||||||||||||||||
|
|
|
. Её обо- |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx dx |
|||||
значают |
d 2 y |
|
и называют производной второго порядка. Аналогично находят |
||||||||||||||||||||||
dx2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d 3 y |
|
d 4 y |
|
|
|
|
|
|
|||||
производные третьего и более высоких порядков ( |
, |
и т.д.). |
|||||||||||||||||||||||
dx3 |
dx4 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Частная производная второго порядка от функции u = f(x,y,z,t) может быть
взята по той же переменной, что и первая ( ∂2u , ∂2u и т.д.) или же по другой
∂x2 ∂y2
переменной ( ∂2u , ∂2u , ...); в последнем случае производная называется сме-
∂x∂y ∂x∂z
шанной. Величина смешанной производной не зависит от порядка переменных,
по которым берутся производные ( ∂2u = ∂2u ). Частные производные более
∂x∂y ∂y∂x
высокого порядка определяются аналогично.
Приложение 3
174

ИНТЕГРАЛ
1. Первообразная функция. Первообразной функцией (или просто первообразной) для данной функции одной переменной y = f (x), определённой в некоторой области, называется такая функция F(x), производная от которой равна dFdx(x) = f (x)
или dF (x) = f (x) dx.
2. Неопределённый интеграл. Общее выражение F(x) + C, где C — произ-
вольная постоянная величина, для всех первообразных от данной функции f (x) называют неопределённым интегралом от функции f (x) или от дифференциала f (x) dx.
Обозначение:
∫ f (x) dx =∫dF (x) = F (x) + C.
Здесь ∫ — знак интеграла, f (x) — подынтегральная функция, dF(x) — подын-
тегральное выражение.
3. Определённым интегралом некоторой функции f(x) на числовом промежутке
b |
lim ∑ f (xi ) xi . Это надо по- |
[a, b] называется следующий предел: ∫ f (x) dx = |
|
a |
xi →0 i |
нимать таким образом. Числовой промежуток [a,b] разбивается на n малых интервалов x1, x2, ... , xn. Длина xi каждого из них умножается на значение функции f(xi) в произвольной точке, находящейся внутри этого малого интервала. Затем составляется сумма ∑ f (xi ) xi и от неё берётся предел при условии, что n стремится к бес-
i
конечности, адлинакаждогомалогоинтервала xi будетстремитьсякнулю. Реально же такой предельный переход провести невозможно по ряду принципи-
альных соображений (например, из-за атомистического строения вещества), атакже вследствие того, что точность измерений уменьшается при уменьшении значения измеряемой величины. Поэтому поступают иным образом. Числовой промежуток
[a, b] разбивается на столь малые интервалы xi, на которых значение функции f (xi) |
|
практически не меняется. Сумму f (xi) |
xi по всем этим интервалам и называют оп- |
ределённыминтеграломотфункцииf (x) начисловомпромежутке[a, b], т.е. |
|
∑ f (xi ) |
b |
xi ≈ ∫ f (x) dx . |
|
i |
a |
Итак, в физике определённый интеграл рассматривается не как предел суммы, а как сумма большого числа достаточно малых слагаемых.
4. Основные правила интегрирования — это свойства неопределённых ин-
тегралов, позволяющие преобразовывать интеграл данной функции к интегралам от других функций:
а) Интегралотмногочленаравенсуммеинтеграловоткаждогослагаемого, т.е.
∫(u +υ − w)dx = ∫u dx +∫υ dx − ∫w dx,
175
где u, υ и w — функции от x.
б) Постоянный множитель C можно выносить за знак интеграла:
∫Cf (x)dx = C∫ f (x)dx.
в) Правило подстановки. Если x = ϕ (t), то ∫ f (x)dx =∫ f (ϕ(t)) ϕ′(t)dt.
г) Интегрированиепочастям: ∫u dυ = uυ − ∫υ du, гдеu, υ — функцииотx. 5. Таблица некоторых интегралов (постоянные интегрирования опущены)
Функция |
Интеграл |
Функция |
Интеграл |
Функция |
Интеграл |
xn |
xn+1/(n+1) |
sin x |
–cos x |
ctg x |
ln |sin x| |
(n≠–1) |
|
|
|
1/cos2x |
|
1/x |
ln x |
сos x |
sin x |
tg x |
|
ex |
ex |
tg x |
–ln |cos x| |
1/sin2x |
–ctg x |
Приложение 4 Вычисление средней скорости теплового движения молекул
Средняя скорость теплового движения молекул находится по формуле:
∞ |
|
−mυ2 |
|
|
|
4 |
|
m |
3 |
|
||||
|
dυ, где |
A = |
2 |
(см. формулу (33.1)). Проведём замену |
||||||||||
υ = A ∫υ3e |
|
2kT |
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
π |
2kT |
|
|
|||
переменной mυ2/(2kT) = |
x. Отсюда υ2 |
= 2kTx/m и υ dυ = (kT/m) dx. Тогда |
||||||||||||
∞ |
2kT |
|
−x kT |
|
kT |
|
2 |
∞ |
−x |
|
||||
υ = A ∫ |
xe |
dx = |
|
∫xe |
dx. Для вычисления этого интеграла |
|||||||||
|
|
|
|
2A |
|
|
|
|
|
|||||
0 |
m |
|
|
|
m |
|
m |
|
|
0 |
|
|
|
|
воспользуемся правилом интегрирования по частям (см. приложение 3, п. 4).
Полагая |
x = u |
и |
|
|
dy = e–x dx, |
y = −∫e−x d(−x) = −e x , |
получаем: |
||||||||
kT |
2 |
|
−x |
∞ |
∞ |
|
−x |
|
kT |
2 ∞ |
−x |
|
–x |
||
υ = 2A |
|
|
− xe |
−∫e |
|
= −2A |
|
∫e |
d (−x), |
||||||
|
0 |
|
|
d (−x) |
|
поскольку –xe |
|||||||||
|
m |
|
|
|
|
0 |
|
|
|
|
m |
0 |
|
|
|
после подстановки пределов интегрирования равна нулю вследствие того, что показательная функция e–x стремится к нулю быстрее, чем стремится к беско-
|
|
|
∞ |
|
|
|
|
|
|
|
kT |
2 |
|
нечности функция x. Находим − ∫e−x d (−x) = − e−x |
0∞=1. |
Тогда υ |
|
||||||||||
= 2A |
. |
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя выражение A, окончательно получаем, что |
|
|
|
|
|
|
|||||||
|
4 |
m |
1 |
|
2 |
4 kT |
|
8kT |
|
|
|
|
|
<υ >= 2 |
m 2 kT |
= |
. |
|
|
|
|||||||
|
|
|
|
= |
π 2m |
πm |
|
|
|
||||
|
π 2kT |
2kT |
m |
|
|
|
|
|
|
||||
Приложение 5
Вычислениесреднегозначенияквадратаскороститепловогодвижениямолекул.
176

Среднее значение <υ2> квадрата скорости молекул находится по формуле
υ2 |
|
1 |
∞ |
|
|
|
mυ2 |
|
= |
∫υ2 dN. Согласно (33.1), dN = ANυ2e |
− 2kT dυ. Тогда |
|
|||||
|
|
N 0 |
|
|
mυ2 |
|
|
|
|
|
|
|
∞ |
− |
|
|
|
|
|
|
<υ2 |
>= A ∫υ4e |
2kT |
dυ. |
(П.5.1) |
|
|
|
|
|
|||||
|
|
|
∞ |
0 |
|
|
|
|
|
|
|
−αυ2 dυ, где α = m/(2kT). |
|
||||
Вычислим сначала интеграл: ∫e |
(П.5.2) |
|||||||
|
|
|
0 |
|
|
|
|
|
Рассмотрим двойной интеграл от функции e−αυ2 −αu 2 по областям (D1), (D2) и (D3), указанным на рис. П.5.1, где (D1) — четверть круга с центром в точке O и радиусом r, (D2) — квадрат, ограниченный прямыми υ = 0, υ = r, u = 0, u = r и (D3) — чет-
верть круга с центром в точке O и радиусом r  2. Из рис. П.5.1 видно, что (D1) являютсячастью(D2), а(D2) частью(D3). Тогдаочевидныследующиенеравенства:
2. Из рис. П.5.1 видно, что (D1) являютсячастью(D2), а(D2) частью(D3). Тогдаочевидныследующиенеравенства:
∫∫e−α(υ2 +u 2 ) dυ du < |
∫∫e−α(υ2 +u 2 ) dυ du < ∫∫e−α(υ2 +u 2 ) dυ du . Введём по- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
(D1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(D2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(D3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
лярные координаты υ = ρcosϕ, u = ρsinϕ. Тогда u2 + υ2 = ρ2, dυdu = ρdρdϕ (см. рис. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
2 |
|
|
|
|
|
π |
2 |
|
π |
ρ |
|
|
|
2 |
|
|
1 |
|
|
|
|
|||||
П.5.2) и ∫∫e−α(υ |
|
+u |
|
) dυ du = |
∫ρe−αρ |
|
|
|
dρ ∫dϕ = |
|
|
∫e−αρ |
|
− |
|
|
d (−αρ2 )= |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
2α |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(D ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
π |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
−αρ2 |
|
r |
|
|
π |
|
|
|
−αr2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= |
|
|
|
|
− |
|
|
e |
|
|
|
|
|
0 |
= |
|
1 |
− e |
|
|
. |
|
|
|
Заменяя |
|
r |
|
на |
|
|
|
r 2 , |
получаем |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
2α |
|
|
|
|
|
|
|
|
4α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
−α(υ2 + u |
2 ) |
|
|
|
|
|
|
|
|
π |
|
|
−2αr2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∫∫e |
|
|
|
|
|
|
|
dυ |
du = |
|
|
|
|
1 |
− e |
|
|
|
|
|
|
. Интегрирование по квадрату (D2) даёт: |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
(D3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫e−α(υ2 +u 2 ) dυ du = ∫e−αυ2 |
dυ ∫e−αu 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(D2 ) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
и написанное выше неравенство |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
принимает вид: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dϕ |
|
|
|
|
|
|
|
|
dρ |
r |
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
−αr |
2 |
|
−αυ |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
− e |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
< |
∫e |
|
|
dυ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
u |
|
|
|
|
r r 2 |
|
|
0 |
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
4α |
|
|
|
π |
|
|
|
|
0 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2αr2 |
|
|
||||||||
|
|
|
|
|
Рис. П.5.1 |
|
|
|
|
|
|
|
|
|
|
Рис. П.5.2 |
|
|
|
|
|
|
|
|
|
− e |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
1 |
|
|
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4α |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При стремлении r к бесконечности крайние члены неравенства стремятся к π/(4α). Следовательно, ктому жепределу должен стремиться исреднийчлен. Изэтогоследуетследующеезначениеинтеграла(П.5.2):
∞ |
1 |
π. |
(П.5.3) |
∫e−αυ2 dυ = |
|||
0 |
2 |
α |
|
|
|
|
177
