
Краткий курс математического анализа. Том 1
.pdf
§ 31. Функциональные последовательности и ряды |
367 |
|
Поскольку z1 + ... + zn0 − n0z0 — фиксированное число, а nlim |
1 |
= |
||||||||||||||||||
|
n |
||||||||||||||||||||
= 0, то существует такой номер m0, |
|
|
|
|
|
|
|
→∞ |
|||||||||||||
что для всех n > m0 выполняется |
|||||||||||||||||||||
неравенство |
|
|
|
z1 + ... + zn0 |
− n0z0 |
|
ε |
|
|
|
|
|
(30.90) |
||||||||
|
|
|
|
|
< |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
Если теперь nε = max {n0, m0} и n > n0, то |
|
|
|
|
|
|
|
|
|
|||||||||||
wn |
z0 |
|
z1 + ... + zn − n0z |
|
+ |
|
(zn0+1 − z0) + ... + (zn − z0) |
|
< |
|
|
||||||||||
| |
− | (30.88) |
|
n |
|
|
|
|
n |
|
|
|
(30.89) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
(30.90) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
ε |
+ |
n − n0 |
ε |
< ε. |
|||||||
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
(30.89) |
|
n |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(30.90) |
|
|
|
|
|
|
|
|
|
|||
Это и означает, что |
lim wn = z0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Те о р е м а 18. Если ряд сходится, то он суммируется методом |
||||||||||||||||||||
средних арифметических к своей сумме. |
|
|
|
|
|
|
|
|
|
||||||||||||
Сходимость ряда |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
un означает, что последовательность его ча- |
||||||||||||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стичных сумм {sn} имеет конечный предел, а тогда, согласно лемме 4, и последовательность средних арифметических {σn} членов последовательности {sn} имеет тот же предел
lim σn = lim sn.
n→∞ n→∞
§31. Функциональные последовательности и ряды
31.1.Сходимость функциональных последовательностей
ирядов. Пусть на некотором множестве X (произвольной природы) задана последовательность функций
fn, n = 1, 2, ..., |
(31.1) |
принимающих числовые значения (вообще говоря, комплексные,
в частности, только действительные). Элементы множества X будем называть точками.
Последовательность (31.1) называется ограниченной на множестве X, если существует такое число c > 0, что для всех n = 1, 2, ...
и всех точек x X выполняется неравенство
|fn(x)| c.
Последовательность (31.1) называется сходящейся на множестве X, если при любом фиксированном x X числовая
последовательность {fn(x)} сходится.
368 |
Гл. 3. Ряды |
Если последовательность (31.1) сходится на множестве X, то функция f , определенная при каждом x X равенством
f (x) def= lim fn(x),
n→∞
называется пределом последовательности (31.1).
Пусть на множестве X задана последовательность числовых функ-
|
∞ |
|
|
ций un(x), n = 1, 2, ... Множество всех числовых рядов |
un(x), |
|
n=1 |
в каждом из которых точка x X произвольно фиксирована, назы- |
||
вается рядом |
∞ |
|
|
|
|
|
un(x) |
(31.2) |
n=1
на множестве X, а функции un(x), n = 1, 2, ..., — его членами. Аналогично случаю числовых рядов сумма
n |
|
|
|
|
x X, |
sn(x) = |
uk (x), |
|
k=1 |
|
|
называется частичной суммой |
ряда |
(31.2) n-го порядка, а ряд |
∞ |
|
|
un+k — его n-м остатком. |
|
|
k=1
Ряд (31.2) называется сходящимся на множестве X, если последовательность {sn(x)} его частичных сумм сходится на этом множестве. При этом предел частичных сумм
lim sn(x) = s(x), x X,
n→∞
называется суммой ряда (31.2). В этом случае пишут
s(x) = ∞ un(x)
n=1
и говорят, что функция s(x) раскладывается в ряд (31.2).
Если ряд (31.2) при любом фиксированном x X сходится абсолютно, то он называется абсолютно сходящимся на множестве X.
П р и м е р ы. 1. Рассмотрим |
ряд, членами которого |
являются |
||||||
функции |
|
|
|
|
||||
un(z) = |
zn |
, |
n = 0, 1, 2, ..., |
|
||||
|
|
|||||||
|
|
|
n! |
|
|
|
|
|
определенные на комплексной плоскости C, т. е. ряд |
|
|||||||
2 |
|
|
|
|
n |
|
||
1 + z + |
z |
+ ... + |
z |
+ ..., z C. |
(31.3) |
|||
2 |
n! |
|||||||

§ 31. Функциональные последовательности и ряды |
369 |
Исследуем абсолютную сходимость этого ряда при фиксированном z с помощью признака Даламбера:
lim |
|un+1(z)| |
= |
lim |z| |
= 0. |
n→∞ |
|un(z)| |
n→∞ n + 1 |
|
|
Таким образом, при любом z C ряд (31.3) абсолютно, а следовательно, и просто сходится; иначе говоря, ряд (31.3) сходится, и притом абсолютно, на всей комплексной плоскости.
2. Рассмотрим ряд
x2 |
|
x2 |
|
x2 |
|
|
|
+ |
|
+ ... + |
|
+ ..., x R. |
(31.4) |
1 + x2 |
(1 + x2)2 |
(1 + x2)n |
||||
При x = 0 все его члены обращаются в нуль и, следовательно, его сумма s(x) также равна нулю:
s(0) = 0. (31.5)
При x = 0 ряд (31.4) представляет собой сумму членов бесконечной геометрической прогрессии со знаменателем
q = |
|
1 |
|
, |
0 < q < 1, |
|
|||
|
2 |
|
|||||||
1 |
+ x |
|
|
|
|
|
|
||
и поэтому |
|
|
|
|
x2 |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
s(x) = |
|
|
1 + x2 |
|
= 1. |
(31.6) |
|||
1 − |
1 |
|
|||||||
|
|
|
|
|
|
||||
|
|
|
1 + x2 |
|
|
||||
Из формул (31.5) и (31.6) следует, что ряд (31.4) сходится на всей
числовой оси и его сумма |
|
|
x = 0% |
| |
| |
0 |
при |
||||
s(x) = |
1 |
при |
x = 0 |
= sign x |
|
оказывается разрывной в точке x = 0 функцией (см. рис. 60), хотя все его члены, очевидно, непрерывны на всей числовой оси.
Этот пример показывает, что сумма сходящегося и даже абсолютно сходящегося на некотором множестве ряда (члены ряда (31.4) неотрицательны, и потому ясно, что он абсолютно сходится), все члены которого непрерывны, может оказаться разрывной функцией. Таким образом, на сходящиеся и даже на абсолютно сходящиеся ряды функций не переносится свойство конечных сумм: сумма конечной совокупности непрерывных на некотором множестве функций также непрерывна на нем. Для того чтобы описать ряды функций, на которые переносится это свойство, введем понятие равномерно сходящихся рядов.
370 |
Гл. 3. Ряды |
31.2. Равномерная сходимость функциональных последовательностей и рядов.
О п р е д е л е н и е 1. Функциональная последовательность (31.1) называется равномерно сходящейся к функции f на множестве X,
если для любого ε > 0 существует такой номер n0, что для всех точек x X и всех номеров n > n0 выполняется неравенство
|fn(x) − f (x)| < ε. |
(31.7) |
fn |
→ |
f def |
ε > 0 |
x |
|
X |
|
n0 |
n > n0 : |
fn(x) |
− |
f (x) |
| |
< ε, |
||
|
|
|
|
|
|
|
| |
|
|
|
||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fn f def |
ε > 0 |
n0 |
|
x |
|
X |
n > n0 : |
fn(x) |
− |
f (x) |
| |
< ε. |
||||
|
X |
|
|
|
|
|
|
|
|
| |
|
|
||||
Таким |
образом, если |
последовательность {fn} только сходится |
||||||||||||||
|
|
|
|
|
|
|
|
|
к |
функции f на множестве X, |
||||||
|
|
|
|
|
|
|
|
|
то |
для каждой точки x X су- |
||||||
ществует, вообще говоря, свой номер n0 = n0(ε, x), для которого при n > n0 выполняется неравенство
|fn(x) − f (x)| < ε,
и может оказаться, что для всех точек x X невозможно подобрать общий номер n0, обладающий указан-
ным свойством.
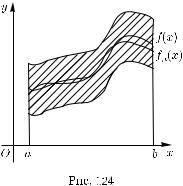
Равномерная же сходимость последовательности {fn} к функции f означает, что, какое бы число ε > 0
ни задать, можно подобрать такой номер n0, что в любой точке x X значение функции fn будет отличаться от значения функции f меньше, чем на ε (рис. 124).
§ 31. Функциональные последовательности и ряды |
371 |
Л е м м а 1. Для того чтобы последовательность {fn} равномерно сходилась на X к функции f , необходимо и достаточно, чтобы
nlim sup |fn(x) − f (x)| = 0. |
(31.8) |
→∞ X |
|
Значение этой леммы состоит в том, что она сводит понятие рав-
номерной сходимости п о с л е д о в а т е л ь н о с т и ф у н к ц и й {fn} к понятию сходимости числовой последовательности
" X | |
n |
(x) |
− |
f (x) |
|# |
sup f |
|
|
|
(«числовой» в широком смысле этого слова: конечное число членов указанной последовательности может обратиться в +∞). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций.
1. Пусть
fn f.
X
Зададим произвольно ε > 0. Тогда существует такой номер n0, что для всех n > n0 и всех x X выполняется неравенство |fn(x) − f (x)| < ε, а следовательно, для всех n > n0 — неравенство
sup |fn(x) − f (x)| ε.
x X
Это и означает выполнение условия (31.8).
2. Пусть выполнено условие (31.8). Зададим произвольно ε > 0. Тогда в силу определения предела числовой последовательности существует такой номер n0, что для всех n > n0 выполняется неравен-
ство
sup |fn(x) − f (x)| < ε,
X
а следовательно, для всех n > n0 и всех x X — неравенство
|fn(x) − f (x)| < ε.
Это означает, что
fn f.
X
С л е д с т в и е. Если существует стремящаяся к нулю последова-
тельность {αn}:
lim αn = 0,
n→∞
такая, что для всех x X выполняется неравенство
|fn(x) − f (x)| αn, |
(31.9) |
то последовательность {fn(x)} равномерно сходится к функции f (x) на множестве X.
372 |
|
|
Гл. 3. Ряды |
|
|
|
|
||
Действительно, поскольку неравенство (31.9) выполняется для |
|||||||||
всех x X, то |
sup |
|
|
− f (x)| αn |
, |
|
|
|
|
|
X |fn(x) |
|
|
|
|
||||
а поэтому из условия lim αn = 0 получаем, что |
|
|
|||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
nlim sup |fn(x) − f (x)| = 0. |
|
|
||||||
|
→∞ X |
|
|
|
|
|
|
|
|
З а м е ч а н и е 1. Очевидно, что из определения равномерной схо- |
|||||||||
димости последовательности функций следует, что если какие-то по- |
|||||||||
следовательности равномерно сходятся на некотором множестве, то |
|||||||||
и любая их конечная линейная комбинация равномерно сходится на |
|||||||||
этом множестве. |
|
|
|
|
|
|
|
|
|
П р и м е р ы. 1. Пусть fn(x) = xn, n = 1, 2, ..., X = [0, q], 0 < q < 1. |
|||||||||
Предел nlim fn(x), |
x [0, q], |
существует и равен нулю: |
|
|
|||||
→∞ |
def |
lim fn(x) = 0. |
|
|
|
||||
|
f (x) = |
|
|
|
|
||||
Так как sup xn = qn, то |
|
n→∞ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
[0,q] |
lim sup xn = lim qn = 0. |
|
|
|
|||||
|
|
|
|
||||||
|
n→∞ [0,q] |
|
|
n→∞ |
|
|
|
|
|
Следовательно, согласно лемме 1, последовательность {xn} равномер- |
|||||||||
но сходится к нулю на отрезке [0, q]: |
|
|
|
|
|
||||
|
xn 0, |
0 < q < 1. |
|
|
|
|
|||
|
[0,q] |
|
|
|
|
|
|
|
|
2. Рассмотрим теперь последовательность функций fn(x) = xn, |
|||||||||
|
|
|
n = 1, 2, ..., на |
полуинтервале X = |
|||||
|
|
|
= [0, 1). Здесь снова |
|
|
||||
|
|
|
|
|
def |
|
|
x [0, 1), |
|
|
|
|
|
f (x) = nlim fn(x) = 0, |
|||||
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
т. е. последовательность {xn} сходит- |
||||||
|
|
|
ся на |
полуинтервале [0, 1) к |
функ- |
||||
|
|
|
ции, |
равной |
нулю: xn |
0,1 0, |
однако |
||
|
|
|
|
|
|
|
[→) |
|
|
|
|
|
sup xn = 1, и потому |
|
|
||||
|
|
|
[0,1) |
|
|
|
|
|
|
|
|
|
|
nlim sup xn |
= nlim 1 = 1 = 0. |
||||
|
|
|
|
→∞ [0,1) |
|
→∞ |
|
|
|
|
Следовательно, |
согласно той же |
лемме сходящаяся на полуинтерва- |
||
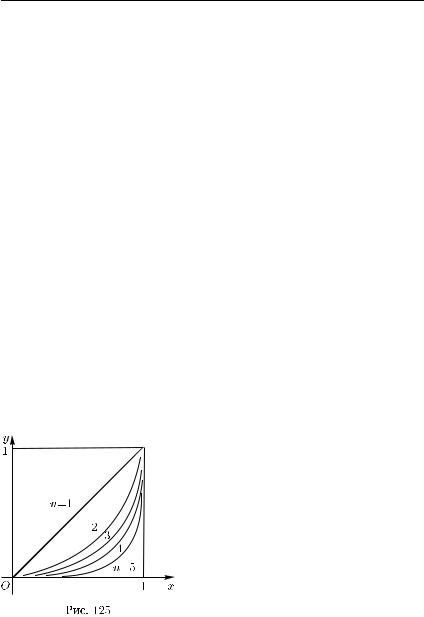
ле [0, 1) последовательность {xn} не сходится на |
нем равномерно |
|
(рис. 125): |
0. |
|
xn |
|
|
|
[0,1) |
|

§ 31. Функциональные последовательности и ряды |
373 |
3. Последовательность fn(x) = xn, n = 1, 2, ..., сходится и на отрезке [0, 1], но уже к разрывной функции
f (x) = lim xn = 0, если 0 x < 1, n→∞ 1, если x = 1.
Поскольку последовательность {xn} не сходится равномерно на полуинтервале [0, 1), то она не сходится равномерно и на отрезке [0, 1]. Это следует из того, что если неравенство (31.7) не выполняется на каком-то множестве X (в данном случае на [0, 1)), то оно, очевидно, не выполняется и на всяком множестве, содержащем в себе X.
Рассмотренная последовательность является еще одним примером сходящейся последовательности непрерывных функций, предел которой уже не является непрерывной функцией (первым примером такого рода у нас была последовательность частичных сумм ряда (31.4)). Ниже будет показано, что если потребовать, чтобы последовательность не только сходилась, но и равномерно сходилась, то подобная ситуация будет уже невозможной (теоремы 7 и 7 ).
Те о р е м а 1 (критерий Коши равномерной сходимости последовательности). Для того чтобы последовательность fn равномерно сходилась на множестве X к некоторой функции, необходимо и достаточно, чтобы для любого ε > 0 существовал такой номер n0, что для всех x X, всех n > n0 и всех p = 0, 1, ... выполнялось неравенство
В символической записи это условие выглядит следующим образом:
ε > 0 n0 |
x X n > n0 |
p 0: |fn+p(x) − fn(x)| < ε. |
|
|
(31.10) |
1. Пусть
fn f.
X
Зафиксируем произвольно ε > 0. Для него в силу (31.7) существует такой номер n0, что для всех n > n0 и всех x X выполняется неравенство
Поэтому для всех точек x X, всех номеров n > n0 и всех p = 0, 1, 2, ...
имеем
|fn+p(x) − fn(x)| = |[fn+p(x) − f (x)] + [f (x) − fn(x)]|
|fn+p(x) − f (x)| + |fn(x) − f (x)| < 2ε + 2ε = ε,
т.е. выполняется условие (31.10).
2.Пусть выполняется условие (31.10); тогда в каждой точке x X последовательность {fn(X)} удовлетворяет критерию Коши сходимо-
374 |
Гл. 3. Ряды |
сти числовых последовательностей и, следовательно, сходится. Обозначим предел последовательности {fn} на множестве X через f :
f (x) = nlim fn(x), x X. |
(31.11) |
→∞ |
|
Перейдя к пределу в последнем неравенстве (31.10) при p → ∞, в силу (31.11) получим, что для всех номеров n > n0 и всех точек x X выполняется неравенство |f (x) − fn(x)| ε.
Это и означает равномерную сходимость последовательности функций {fn} к функции f на множестве X.
О п р е д е л е н и е 2. Ряд |
|
∞ |
|
|
|
un(x), x X, |
(31.12) |
n=1
называется равномерно сходящимся на множестве x, если на x равномерно сходится последовательность его частичных сумм.
Очевидно, что ряд, равномерно сходящийся на множестве X, сходится на этом множестве. Пусть
|
∞ |
|
|
n |
|
|
|
|
|
|
|
s(x) = |
un(x), |
sn(x) = |
uk (x) |
||
|
n=1 |
k |
|
k=1 |
|
и rn(x) = s(x) − sn(x) = |
uk (x) — остаток ряда. Равномерная |
||||
=n+1 |
|||||
|
∞ |
|
|
||
|
|
|
|
||
|
|
|
|
|
|
сходимость ряда |
un(x) согласно определению означает, что |
||||
|
n=1 |
|
|
|
|
|
|
sn(x) s(x). |
(31.13) |
||
|
|
|
X |
|
|
Это условие равносильно условию
s(x) − sn(x) 0.
X
Поэтому условие (31.13) равномерной сходимости на множестве X ряда равносильно условию
rn(x) 0. |
(31.14) |
X |
|
Иначе говоря, равномерная сходимость ряда на множестве X означает равномерную сходимость на X к нулю последовательности его остатков. Отсюда в силу леммы получаем, что для того чтобы ряд (31.12) равномерно сходился на множестве X, необходимо и достаточно, чтобы
nlim sup |rn(x)| = 0. |
(31.15) |
→∞ X |
|
§ 31. Функциональные последовательности и ряды |
375 |
З а м е ч а н и е 2. Если какие-то ряды равномерно сходятся |
на |
некотором множестве, то и любая их конечная линейная комбинация равномерно сходится на этом множестве (см. замечание 1).
Те о р е м а 2 (необходимое условие равномерной сходимости ряда).
Если ряд (31.12) равномерно сходится на множестве X, то последовательность его членов равномерно стремится к нулю на этом множестве.
В самом деле,
un(x) = sn(x) − sn−1(x), n = 2, 3, ... |
(31.16) |
В случае равномерной сходимости на множестве X ряда (31.12) после-
довательности {sn(x)} и {sn−1(x)} его частичных сумм равномерно |
|||||||
стремятся на X к его сумме s(x): |
|
|
|
|
|
||
sn(x) s(x), |
|
sn |
− |
1(x) s(x), |
|
||
X |
|
|
|
|
X |
|
|
поэтому |
|
|
|
1(x) 0, |
|
||
sn(x) |
− |
sn |
− |
|
|||
|
|
|
|
X |
|
||
а это в силу (31.16) и означает, что |
|
|
|
|
|||
un(x) 0. |
(31.17) |
||||||
|
|
X |
|
|
|
|
|
Отметим, что согласно лемме 1 для того, чтобы было выполнено условие (31.17), необходимо и достаточно, чтобы выполнялось условие
nlim sup |un(x)| = 0. |
(31.18) |
→∞ X |
|
Те о р е м а 3 (критерий Коши равномерной сходимости ряда). Для того чтобы ряд (31.12) равномерно сходился на множестве X, необходимо и достаточно, чтобы для любого ε > 0 существовал такой номер n0, что для всех n > n0, всех p = 0, 1, 2, ... и всех x X выполнялось неравенство
|un(x) + un+1(x) + ... + un+p(x)| < ε.
В силу равенства
un(x) + un+1(x) + ... + un+p(x) = sn+p(x) − sn−1(x),
где sn(x) — частичные суммы рассматриваемого ряда, критерий Коши равномерной сходимости рядов сразу следует из критерия Коши равномерной сходимости последовательностей.
З а м е ч а н и е 3. В дальнейшем нам понадобится следующее простое свойство равномерно сходящихся рядов.

376 Гл. 3. Ряды
Если ряд (31.12) равномерно сходится на множестве X, а функция f ограничена на этом множестве, то ряд ∞ f (x)un(x) также
n=1
равномерно сходится на X.
Действительно, ограниченность функции f означает, что существует такая постоянная c > 0, что для всех x X выполняется неравенство |f (x)| c. Поэтому для любых целых n 1, p 0 и любой точки x X имеет место неравенство
|f (x)un(x) + f (x)un+1(x) + ... + f (x)un+p(x)| =
=|f (x)||un(x) + un+1(x) + ... + un+p(x)|
c|un(x) + un+1(x) + ... + un+p(x)|.
Из этого неравенства следует, что ряд ∞ f (x)un(x) удовлетворяет
n=1
на множестве X критерию Коши равномерной сходимости ряда, ибо этому критерию удовлетворяет исходный ряд (31.12).
Те о р е м а 4 (признак Вейерштрасса). Если числовой ряд
∞ |
|
|
|
αn, αn 0, |
(31.19) |
n=1 |
|
сходится и для всех x X и для всех n = 1, 2, ... |
выполняется |
неравенство |
|
|un(x)| αn, |
(31.20) |
то ряд (31.12) абсолютно и равномерно сходится на множестве X.
Абсолютная сходимость ряда (31.12) в каждой точке x множества X следует, согласно признаку сравнения (теорема 6 в п. 30.4), из неравенства (31.20) и сходимости ряда (31.19).
|
Докажем равномерную сходимость ряда (31.12). Пусть rn(x) и εn |
|||||
|
|
|
|
|
|
∞ |
являются остатками порядка n соответственно рядов un(x), x X, |
||||||
|
∞ |
∞ |
|
|
∞ |
n=1 |
и |
|
|
|
k |
|
αk . Тогда |
αn, т. е. rn(x) = |
uk(x), |
εn = |
|
|||
|
n=1 |
k=n+1 |
|
|
=n+1 |
|
|
∞ |
∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|uk (x)| (31.20) k=n+1 αk = εn, x X. |
|||
|
|rn(x)| = k=n+1 uk (x) k=n+1 |
|||||
