§ 22. Интегрирование некоторых трансцендентных функций |
257 |
3. α + λ — ц е л о е ч и с л о. Пусть, как и выше, α = m/n, где |
m и n > 0 |
— целые числа. Имеем (a + bt)αtλ dt = |
a + bt |
α |
|
tα+λ dt. |
t |
Снова получился интеграл типа, рассмотренного в п. 21.1: под- |
|
|
|
|
|
|
становка |
u = |
a + bt |
1/n |
|
|
|
|
функции. |
|
t |
сводит его к интегралу от рациональной |
Итак, в трех случаях, когда α, λ или α + λ являются целыми числами, интеграл (21.7) сводится к интегралу от рациональных функций.
|
Поэтому если хотя бы одно из чисел α, |
γ + 1 |
или |
γ + 1 |
+ α в перво- |
|
β |
β |
|
|
|
|
начальном интеграле (21.4) является целым числом, то этот интеграл сводится к интегралу от рациональных функций и, следовательно, выражается через элементарные функции.
Русский математик П. Л. Чебышев 1) показал, что ни в каком другом случае рациональных показателей α, β и γ интеграл (21.4) не выражается через элементарные функции.
§ 22. Интегрирование некоторых трансцендентных функций
22.1. Интегралы |
|
|
|
|
|
R(sin x, cos x) dx. |
|
|
Интеграл R(sin x, |
cos x) dx сводится подстановкой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = tg |
x |
, −π < x < π, |
|
|
|
|
|
|
(22.1) |
2 |
|
|
|
|
|
|
к интегралу от рациональной функции. Действительно, |
|
|
|
2 sin |
x |
|
cos |
x |
|
|
|
|
|
2tg |
x |
|
|
|
|
|
|
|
2u |
|
sin x = |
2 |
2 |
|
= |
2 |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
2 x |
|
|
|
|
|
2 x |
|
2 x |
+ 1 |
|
|
1 |
2 |
|
|
sin |
|
|
|
|
|
|
+ cos |
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
+ u |
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
cos2 |
x |
− sin2 |
x |
|
|
|
1 − tg 2 |
x |
|
|
|
|
1 |
|
u2 |
|
|
2 |
2 |
|
|
2 |
|
|
|
cos x = |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
− 2 |
, |
|
|
2 x |
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
2 x |
|
|
|
|
sin |
|
|
|
+ cos |
|
|
|
|
|
1 + tg |
|
|
|
|
|
|
|
1 + u |
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
x = 2 arctg u, |
|
dx = |
|
|
2 du |
|
, |
|
|
|
|
|
|
1 + u |
2 |
|
|
|
|
|
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + u2 |
|
|
1 + u2 1 + u2 |
|
R(sin x, cos x) dx = 2 |
|
R |
2u |
|
|
|
, |
1 − u2 |
|
du |
, |
|
|
|
|
|
|
|
|
|
|
т. е. получился интеграл от рациональной функции. |
|
При вычислении интегралов типа |
|
R(sin x, cos x) dx часто оказы- |
ваются полезными также и подстановки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = sin x, |
|
u = cos x, |
|
|
|
u = tg x. |
|
|
|
(22.2) |
1) П. Л. Чебышев (1821–1894) — русский математик.
258 Гл. 2. Интегральное исчисление функций одной переменной
В ряде случаев при интегрировании с помощью этих подстановок требуется провести меньше вычислений, чем при интегрировании с помощью подстановки (22.1).
П р и м е р ы. 1. Применим подстановку (22.1) для вычисления интеграла
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем |
|
|
|
|
|
|
|
|
|
1 − sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= 2 |
|
|
|
|
du |
|
= |
2 |
|
|
|
du |
|
|
= |
|
|
2 |
|
|
+ C = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
sin x |
|
|
|
2u |
2 |
|
|
|
|
2 |
|
1 |
|
u |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
1 − |
|
(1 + u ) |
|
|
(1 |
− u) |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + u2 |
|
|
|
|
|
|
|
= |
2 |
|
|
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − tg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2. Для вычисления интеграла |
|
dx |
|
применим подстановку u = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= tg x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos6 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= |
1 |
|
|
d(tg x) = (1 + tg 2x)2 d(tg x) = |
(1 + u2)2 du = |
|
|
|
|
|
|
|
|
|
|
cos6 x |
|
cos4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (1 + 2u2 + u4) du = u + |
2u3 |
+ |
u5 |
+ C = tg x + |
2 tg 3x |
+ |
tg 5 x |
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
|
|
22.2. Интегралы |
sinm x cosn x dx. В случае когда m и n — |
рациональные |
числа, |
интеграл |
|
sinm x cosn x dx подстановкой u = |
= sin x или v = cos x сводится к интегралу от иррациональной функции, а именно к интегралу от дифференциального бинома (п. 21.3).
В самом деле, если, например, u = sin x, то
dx = du = (1 − u2)−1/2 du cos x
и, следовательно,
sinm x cosn x dx = um(1 − u2)(n−1)/2 du,
т. е. действительно получился интеграл от дифференциального бинома и, таким образом, выражается ли он через элементарные функции, зависит от того, какие при этом получились показатели степеней (см. п. 21.3 ).
В случае когда m и n — целые числа, интеграл sinm x cosn x dx относится к типу интегралов, рассмотренных в предыдущем пункте, и для его вычисления целесообразно использовать подстановки (22.2).

§ 22. Интегрирование некоторых трансцендентных функций |
259 |
Например,
|
sin3 x |
dx = |
− |
|
sin2 x |
d cos x = |
− |
|
1 − cos2 x |
|
d cos x |
= |
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
cos2 x |
|
|
|
|
|
|
cos2 x |
|
|
|
u=cos x |
|
|
|
|
= |
|
|
|
1 − u2 |
du = |
du |
− |
|
du |
= u + |
|
1 |
+ C = cos x + |
1 |
+ C. |
|
|
|
|
|
|
|
|
|
u=cos x − |
u2 |
|
|
|
|
|
|
u2 |
|
u |
|
cos x |
|
Если |
|
m = 2k + 1 |
|
и |
n = 2l + 1 — нечетные числа, то полезна |
подстановка t = cos 2x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2k+1 x cos2l+1 x dx = |
1 |
|
sin2k x cos2l x sin 2x dx = |
|
|
2 |
|
|
= −4 |
|
|
− |
2 |
|
|
2 |
|
d cos 2x = −2k+l+2 |
(1 − t)k(1 + t)l dt, |
1 |
|
|
1 |
|
cos 2x k |
1 |
+ cos 2x |
l |
|
|
|
1 |
|
|
|
т. е. получился интеграл от рациональной дроби (k и l могут быть отрицательными).
Если m и n — четные числа, то полезна подстановка u = tg x — см. пример 2 в п. 22.1.
Если оба показателя m и n неотрицательные и четные, то, приме-
нив формулы sin2 x = |
1 − cos 2x |
, cos2 x = |
1 + cos 2x , получим интеграл |
|
|
2 |
|
|
|
2 |
|
|
|
того же типа, но с меньшими показателями, например, |
|
sin2 x dx = |
|
1 − cos 2x |
dx = |
x |
|
sin 2x |
+ C. |
|
|
2 − |
4 |
|
|
|
2 |
|
|
|
|
Отметим, что методами, аналогичными |
методам, описанным |
в этом пункте, берутся интегралы вида |
sh mx ch nx dx. |
|
22.3. Интегралы sin αx cos βx dx, |
sin αx sin βx dx, |
cos αx× |
× cos βx dx. Интегралы |
|
sin αx cos βx dx, sin αx sin βx dx, |
cos αx × |
× cos βx dx вычисляются, если их подынтегральные выражения преобразовать по формулам
sin αx cos βx = 12 [sin(α + β)x + sin(α − β)x], sin αx sin βx = 12 [cos(α − β)x − cos(α + β)x], cos αx cos βx = 12 [cos(α + β)x + cos(α − β)x].
Например,
sin x cos 2x dx = 12 sin 3x dx − 12 sin x dx = −16 cos 3x + 12 cos x + C.
260Гл. 2. Интегральное исчисление функций одной переменной
22.4.Интегралы от трансцендентных функций, вычисляющиеся с помощью интегрирования по частям. К интегра-
лам от трансцендентных функций, вычисляющимся с помощью интегрирования по частям, относится много разнообразных интегралов, например,
|
|
|
|
|
|
eαx cos βx dx, |
eαx sin βx dx, |
xn cos αx dx, |
xn sin αx dx, |
xneαx dx, |
xn arcsin x dx, |
xn arccos x dx, |
xnarctg x dx, |
xnarcctg x dx, |
xn ln x dx. |
Здесь везде n — целое неотрицательное число.
Для вычисления интегралов eαx cos βx dx и eαx sin βx dx следует их дважды проинтегрировать по частям, в результате для каждого из них получится линейное уравнение, из которого они сразу находятся. Например,
I = eαx sin βx dx = − |
1 |
|
eαxd cos βx = |
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
= − |
eαx cos βx |
|
|
α |
|
|
|
|
|
|
|
|
eαx cos βx |
|
α |
|
|
|
|
|
|
|
|
+ |
|
|
eαx cos βx dx = − |
|
|
|
+ |
|
eαxd sin βx = |
β |
|
|
|
|
|
β |
|
β |
β2 |
|
|
|
|
αx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
cos βx |
α |
|
αx |
|
|
αx |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
β |
|
|
+ β2 |
sin βx − α e |
sin βx dx αx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (α sin βx − β cos βx) e |
− |
α I; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β2 |
β2 |
|
отсюда I = |
α sin βx − β cos βx |
eαx |
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α2 + β2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В интегралах |
|
xn cos αx dx, |
xn sin αx dx, |
xneαx dx после одно- |
кратного интегрирования по частям получаются интегралы тех же типов, но с меньшими показателями степени.
|
|
|
|
|
Рассмотрим пример: |
|
|
x sin x dx = − |
x d cos x = −x cos x + |
cos x dx = −x cos x + sin x + C. |
В интегралах |
xn arcsin x dx, |
xn arccos x dx, |
xn arctg x dx, |
xn arcctg x dx, |
xn ln x dx в результате однократного интегрирования |
по частям пропадает трансцендентная функция, причем в первых двух получаются интегралы от иррациональных функций, выражающиеся через элементарные функции, а в трех последних — интегралы

§ 23. Определенный интеграл |
261 |
от рациональных функций и, следовательно, также выражающиеся через элементарные функции. Например,
arcsin x dx = x arcsin x − |
|
|
x dx |
|
= |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
1 |
|
|
1/2 |
|
|
|
2 |
|
1 − x |
2 |
|
= x arcsin x + |
|
(1 − x )− |
|
d(1 |
− x |
) = x arcsin x + |
|
+ C. |
2 |
|
|
В заключение подчеркнем, что далеко не всякий интеграл от элементарной функции выражается через элементарные функции. Среди таких интегралов встречаются интегралы, которые находят большое применение в различных разделах математики. К числу их относятся,
например, вероятностный интеграл e−x2 dx, интегральный логарифм
dx |
|
, интегральный синус |
sin x |
dx. |
ln x |
|
|
x |
§23. Определенный интеграл
23.1.Определенный интеграл Римана 1). Напомним, что множество τ = {xk}kk==k0τ точек отрезка [a, b] таких, что
a = x0 < x1 < ... < xkτ −1 < xkτ = b,
называется разбиением отрезка [a, b], a R, b R.
Точки xk называются точками разбиения τ , отрезки [xk−1, xk ] —
отрезками разбиения τ ; их длины обозначаются xk , |
т. е. xk = |
= xk − xk−1, |
k = 1, 2, ..., kτ (ясно, что количество точек разбиения на |
единицу больше числа отрезков разбиения), а число |
|
|
def |
x1, x2, ..., |
xkτ } |
|
|
|τ | = max { |
|
называемся мелкостью разбиения τ. |
|
|
Разбиение |
τ = {xk }kk==0kτ |
называется |
разбиением, |
вписанным |
в разбиение |
τ , если τ τ , |
т. е. если каждая точка разбиения τ |
содержится в разбиении τ . В этом случае каждый отрезок [xk−1, xk ]
разбиения содержится в некотором отрезке [xj−1, xj ] разбиения τ , j = 1, 2, ..., kτ .
Разбиение τ , вписанное в разбиение τ , называется также разбиением, следующим за разбиением τ , и пишут τ τ. В этом случае говорят также, что разбиение τ предшествует разбиению τ , и пишут
τ τ .
Существенными являются следующие два с в о й с т в а р а з б и е-
н и й о т р е з к а.
1◦. Если τ τ , а τ τ , то τ τ .
1) Б. Риман (1826–1866) — немецкий математик.
262 Гл. 2. Интегральное исчисление функций одной переменной
Действительно, если каждый отрезок разбиения τ содержится в некотором отрезке разбиения τ , а каждый отрезок разбиения τ содержится в некотором отрезке разбиения τ , то каждый отрезок
разбиения τ содержится в соответствующем отрезке разбиения τ.
2◦. Для любых разбиений τ и τ существует такое разбиение τ ,
что τ τ и τ τ .
В самом деле, таким разбиением является, например, разбиение, состоящее из всех точек обоих разбиений τ и τ .
Пусть функция f определена на отрезке [a, b], a < b, и τ = = {xk}kk==k0τ — некоторое разбиение этого отрезка. Всякая сумма στ
вида
στ = στ (f ; ξ1, ..., ξkτ ) def= kτ f (ξk)Δxk ,
k=1
ξk [xk−1, xk], k = 1, 2, ..., kτ ,
называется интегральной суммой Римана функции f.
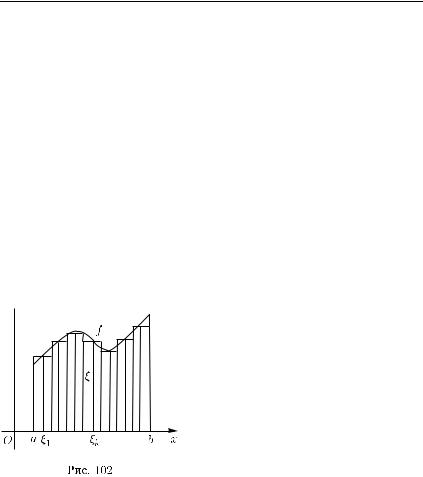
В случае если функция f неотрицательна, то интегральная сумма στ равна площади фигуры, со-  ставленной из прямоугольников с основанием [xk−1, xk] и высотой длины
ставленной из прямоугольников с основанием [xk−1, xk] и высотой длины
f (ξk) (рис. 102).
О п р е д е л е н и е 1. Функция f
называется интегрируемой по Риману на отрезке [a, b], если для любой
последовательности разбиений
τn = {x(kn)}kk==k0τn , n = 1, 2, ...,
любого выбора точек ξk(n) ности интегральных сумм
отрезка [a, b], мелкость которых стре-
мится к нулю: lim |τn| = 0, и для
n→∞
[x(kn−)1, x(kn)], k = 1, 2, ..., kτ , последователь-
(n) |
(n) |
στn (f ; ξ1 |
, ..., ξkτn ), n = 1, 2, ..., |
имеют и притом один и тот же предел.
Этот предел называется интегралом Римана функции f по отрез-
b
ку [a, b]. Его обозначают f (x) dx и пишут
a
b
lim στ = f (x) dx. |
(23.1) |
|τ |→0 |
|
|
§ 23. Определенный интеграл |
263 |
Согласно определению это означает, что если |
|
kτn |
f (ξk(n))Δxk(n), ξk(n) [xk(n−)1, xk(n)], |
xk(n) = xk(n) − xk(n−)1, |
στn = |
k=1 |
k = 1, 2, ..., kτn , |
|
|
|
то |
|
b |
|
|
|
|
|
(n) |
(n) |
|
|
lim στn (f ; ξ1 |
, ..., ξkτn ) = f (x) dx, |
|
n→∞ |
a |
|
|
|
|
если только lim |τn| = 0.
n→∞
Можно сформулировать определение интеграла Римана и не используя понятия предела последовательности, а, как говорят, на «язы-
ке ε–δ».
О п р е д е л е н и е 2. Число I называется интегралом Римана от функции f на отрезке [a, b], если для любого ε > 0 существует такое
δ > 0, что, каково бы ни было разбиение τ = {xk}kk==k0τ отрезка [a, b], мелкость которого меньше δ : |τ | < δ, и каковы бы ни были точки ξk [xk−1, xk ], k = 1, 2, ..., kτ , выполняется неравенство
|στ (f ; ξ1, ..., ξkτ ) − I| < ε.
Аналогично равносильности определений предела функции в терминах последовательностей и в терминах окрестностей доказывается и равносильность определений 1 и 2 интеграла Римана. Это рекомен-
дуется читателю проделать самостоятельно.
b
В интеграле f (x) dx число a называется нижним, а число b —
a
верхним пределом интегрирования.
В дальнейшем для краткости вместо «функция, интегрируемая по Риману», будем говорить «интегрируемая функция», а вместо «интеграл Римана» — просто «интеграл».
Дополним определение интеграла следующими соглашениями.
a Если функция f задана в точке x = a, то по определению
f (x) dx = 0. Если функция f |
интегрируема на отрезке [a, b], |
a |
|
|
то положим |
a |
b |
|
|
def |
|
f (x) dx = |
− f (x) dx. |
|
b |
a |
23.2. Ограниченность интегрируемых функций. Изучение определенного интеграла начнем с исследования необходимых, а затем и достаточных условий интегрируемости функций.
264Гл. 2. Интегральное исчисление функций одной переменной
Те о р е м а 1. Если функция интегрируема на некотором отрезке, то она ограничена на нем.
b
Пусть функция f интегрируема на отрезке [a, b] и f (x) dx = I.
a
Зафиксируем какое-либо ε > 0, например ε = 1. Согласно определению 2 интеграла существует такое δ > 0, что для любой интегральной суммы στ , соответствующей разбиению τ мелкости |τ | < δ, выполняется неравенство |δτ − I| < 1, а следовательно, и неравенство
I − 1 < στ < I + 1, |
(23.2) |
т. е. множество {στ } значений интегральных сумм στ , |τ | < δ, функции f ограничено.
Допустим теперь, что существует функция f , интегрируемая на некотором отрезке [a, b], и неограниченная на этом отрезке. Возьмем произвольное разбиение τ = {xk}kk==k0τ отрезка [a, b]. Из того, что функция f неограниченна на отрезке [a, b], следует, что она неограниченна и по крайней мере на одном из отрезков разбиения τ. Пусть для определенности функция f неограниченна на отрезке [x0, x1]. Из ее неограниченности на этом отрезке следует, что для любого числа n на нем существует такая точка, обозначим ее ξ1(n), что
|f (ξ1(n))| > n, ξ1(n) [x0, x1], |
n = 1, 2, ... |
Отсюда, очевидно, следует, что |
|
nlim f (ξ1(n)) = ∞. |
(23.3) |
→∞ |
|
Зафиксируем какие-либо точки ξk в остальных отрезках разбие-
ния τ : |
|
ξk [xk−1, xk], k = 2, 3, ..., kτ . |
|
Тогда сумма |
|
kτ |
|
|
|
f (ξk )Δxk |
(23.4) |
k=2
будет иметь вполне определенное значение. Добавив к этой сум-
ме слагаемое f (ξ1(n))Δx1, |
получим |
интегральную |
сумму |
στ(n) = |
= στ (f ; ξ1(n), ξ2, ..., ξk ), причем в силу условия (23.3) и постоянства |
суммы (23.4) будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kτ |
|
|
k |
|
|
lim σ |
|
(f ; ξ(n), |
|
|
|
|
lim |
(n) |
|
|
)Δx |
|
|
|
|
, |
, |
|
f (ξ |
|
= ∞ |
, |
n→∞ |
τ |
1 |
ξ2 |
|
... |
ξkτ ) = n→∞ f (ξ1 |
)Δx1 + k=2 |
k |
|
|
а следовательно, для л ю б о г о разбиения τ множество значений интегральных сумм στ(n) неограниченно. Поэтому неограниченно и мно-

§ 23. Определенный интеграл |
265 |
жество {στ }, |τ | < δ (число δ > 0 было выбрано выше), что противоречит неравенству (23.2).
З а м е ч а н и е. Условие ограниченности функции, являясь необходимым условием интегрируемости функции по Риману, не является достаточным условием для этого. В самом деле, рассмотрим, напри-
мер, функцию Дирихле |
|
1, |
если x рационально, |
f (x) = 0, |
если x иррационально. |
Каковы бы ни были отрезок [a, b] и его разбиение τ = {xk }kk==k0τ , выбрав все точки ξk [xk−1, xk ] рациональными, в силу условия f (ξk) = 1, k = 1, 2, ..., kτ , получим
|
k=τ |
|
|
στ (f ; ξ1, ..., ξkτ ) = |
xk = b − a, |
|
k=1 |
а выбрав точки ξk иррациональными, в силу условия f (ξk) = 0, k = = 1, 2, ..., kτ , будем иметь
|
kτ |
|
|
στ (f ; ξ1, ..., ξkτ ) = |
0 · xk = 0. |
|
k=1 |
Поэтому интегральные суммы στ функции Дирихле заведомо не имеют предела при |τ | → 0.
Тем самым функция Дирихле дает пример функции, ограниченной на любом отрезке, но неинтегрируемой на нем.
23.3. Верхние и нижние суммы Дарбу 1). Пусть функция f
определена на отрезке [a, b], τ = {xk}kk==0kτ — разбиение этого отрезка, |
k = [xk−1, xk ], |
|
xk = xk − xk−1. Положим |
|
|
Mk = |
sup f (x), |
mk = |
inf |
f (x), k = 1, 2, ..., kτ , |
(23.5) |
|
x |
k |
x |
k |
|
|
|
|
kτ |
|
|
|
kτ |
|
|
|
|
|
|
|
|
|
Sτ = Sτ (f ) = |
Mk xk , |
sτ = sτ (f ) = |
mk xk . |
(23.6) |
|
|
k=1 |
|
|
|
k=1 |
|
Сумма Sτ , называется верхней, а сумма sτ — нижней суммой Дарбу функции f. Очевидно, что в случае, когда функция f ограничена, то нижние mk и верхние Mk грани (23.5) конечны, и потому суммы Дарбу (23.6) при любом разбиении принимают конечные значения. В дальнейшем будем предполагать, что функция f ограниченна — это естественно, так как нас будут интересовать свойства интеграла от функции f , а он, согласно теореме 1, может существовать только в том случае, когда функция ограниченна.
1) Г. Дарбу (1842–1917) — французский математик.

266 Гл. 2. Интегральное исчисление функций одной переменной
Из того, что выполняется неравенство mk Mk, k = 1, 2, ..., kτ ,
следует, что при любом разбиении τ выполняется неравенство |
|
|
|
|
|
|
|
|
sτ Sτ . |
|
|
|
(23.7) |
|
Очевидно также, что в силу определения (23.5) чисел mk и Mk для |
любых ξk |
k имеет место неравенство |
|
|
|
|
|
|
|
|
|
mk f (ξk) Mk , |
k = 1, 2, ..., kτ . |
|
|
|
|
Отсюда следует справедливость неравенства |
|
|
|
|
|
|
|
|
|
sτ στ ≡ στ (f ; ξ1, ..., ξkτ ) Sτ . |
|
(23.8) |
|
Отметим еще следующие с в о й с т в а |
с у м м Д а р б у. |
|
|
|
|
1◦. Каждая нижняя сумма Дарбу не превосходит любой верхней: |
|
|
|
|
|
|
sτ1 Sτ2 |
|
|
|
(23.9) |
(τ1 и τ2 — разбиения отрезка [a, b]). |
|
|
|
|
|
|
Пусть сначала τ τ , τ = {xk }kk==0kτ , |
τ = {xj }jj |
==1jτ — разбиения |
отрезка [a, b], |
|
|
|
|
|
|
|
|
|
|
|
|
= inf |
f (x), |
k = [xk−1, xk], |
j = [xj−1, xj ], |
j = 1, 2, |
|
, j |
|
m |
|
k = 1, 2, |
... |
, k , |
m = |
inf |
f (x), |
... |
. |
|
k |
x k |
|
|
τ |
j |
x |
j |
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие τ τ |
означает, что каждый отрезок |
k разбиения τ |
является объединением некоторых отрезков разбиения τ . Обозначим
эти отрезки jk , тогда |
k = |
jk |
jk , где суммирование ведется по всем |
таким индексам jk , что |
j |
k . Отсюда следует, что |
|
|
k |
|
|
|
|
|
|
xk = jk |
xjk . |
(23.10) |
Кроме того, выполняются неравенства |
|
|
|
mk mjk , |
(23.11) |
так как при переходе от отрезка k |
к содержащемуся в нем отрез- |
ку jk нижняя грань значений функции может только увеличиваться.
Теперь легко доказать неравенство |
|
|
|
|
В самом деле, |
|
|
sτ sτ . |
|
|
|
(23.12) |
|
|
|
|
|
|
|
sτ = mk xk = |
mk |
|
xjk |
|
|
mjk xjk = |
(23.10) |
k |
j |
(23.11) |
k |
j |
|
k |
|
|
|
|
|
k |
|
k |
mj xj = sτ . |
|
|
|
|
|
|
= |










 ставленной из прямоугольников с основанием [
ставленной из прямоугольников с основанием [