
Краткий курс математического анализа. Том 1
.pdf§ 24. Свойства интегрируемых функций |
277 |
в неравенстве (24.9) к верхним граням по всевозможным x [xk−1, xk ] и x [xk−1, xk ], получим
ωk (f g) A[ωk(f ) + ωk (g)], k = 1, 2, ..., kτ ;
здесь ωk (·), как обычно, — колебание соответствующей функции на отрезке [xk−1, xk ]. Отсюда
kτ |
kτ |
kτ |
!. |
|
|
|
|
|
|
k=1 ωk (f g)Δxk A |
k=1 ωk (f )Δxk + k=1 ωk (g)Δxk |
(24.10) |
||
В силу интегрируемости функций f и g на отрезке [a, b] имеем (см. (23.21))
|
kτ |
|
|
kτ |
|
|
lim |
ω(f )Δxk = lim |
ωk (g)Δxk = 0. |
||||
| |→ |
|
| |→ |
|
|
|
|
τ |
0 k=1 |
τ |
0 k=1 |
|
|
|
|
|
|
|
|
|
kτ |
Поэтому из неравенства (24.10) следует, что lim |
ωk (f g)Δxk = 0, |
|||||
|
|
|
|
| |→ |
|
|
|
|
|
|
τ |
0 k=1 |
|
откуда в силу того же критерия (23.21) и вытекает интегрируемость произведения f g.
6◦. И н т е г р и р о в а н и е ч а с т н о г о и н т е г р и р уе м ы х ф у н к- ц и й. Если функции f и g интегрируемы на некотором отрезке и абсолютная величина функции g ограничена на нем снизу положи-
тельной постоянной, то частное |
f |
также интегрируемо на этом |
|||
g |
|||||
отрезке. |
|
|
|
||
|
|
1 |
|
||
Покажем, что при сделанных предположениях функция |
инте- |
||||
g |
|||||
грируема. Пусть функция g интегрируема на отрезке [a, b] и существу-
ет такая постоянная c > 0, что для всех точек x [a, b] выполняется неравенство |g(x)| c. Тогда для любых точек x, x [a, b] имеем
|
1 |
1 |
|
= g(x) − g(x ) |
|
1 g(x) g(x ) . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||g(x )||g(x)|| c2 | |
− |
| |
|||||
g(x ) |
− g(x) |
|
|||||||||
Если τ = {xk}kk==k0τ — разбиение отрезка [a, b] и точки x, x содержатся в одном и том же отрезке [xk−1, xk], k = 1, 2, ..., kτ , разбиения τ , то переходя к верхним граням в полученном неравенстве, будем иметь
|
|
ωk g |
c2 ωk (g). |
|
|||||
|
|
|
|
1 |
|
|
1 |
|
|
Отсюда |
1 |
|
|
|
1 |
kτ |
|
||
kτ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(g)Δxk. |
k=1 ωk |
g |
xk |
c2 |
k=0 ωk |
|||||
В силу интегрируемости функции g правая часть неравенства стремится к нулю при |τ | → 0. Поэтому стремится к нулю и его левая

278 Гл. 2. Интегральное исчисление функций одной переменной
часть. Это означает интегрируемость функции |
1 |
|
на отрезке [a, b]. |
|||||||
g |
||||||||||
|
|
|
|
|
|
f |
|
|||
Если функция f также интегрируема на этом отрезке, то частное |
, |
|||||||||
|
||||||||||
|
|
|
|
|
1 |
|
g |
|||
будучи произведением интегрируемых функций f и |
, согласно свой- |
|||||||||
|
g |
|||||||||
ству 5◦ также интегрируемо. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
7◦. И н т е г р и р о в а н и е н е р а в е н с т в. Если функции f и g |
|||||||||
интегрируемы на отрезке [a, b] и |
|
|
|
|
|
|
|
|
||
то |
f (x) g(x), x [a, b], |
|
|
|
|
(24.11) |
||||
b |
b |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
f (x) dx |
g(x) dx. |
|
|
|
|
(24.12) |
|||
|
a |
a |
|
|
|
|
|
|
|
|
|
В частности, если f (x) 0, x [a, b], то |
|
|
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
f (x) dx 0. |
|
|
|
|
(24.13) |
||||
a
Из неравенства (24.11) следует, что для любых интегральных сумм στ (f ) и στ (g) соответственно функций f и g выполняется неравенство
kτ |
|
kτ |
|
|
f (ξk)Δxk |
|
|
στ (f ) = |
g(ξk)Δxk = στ (g), |
(24.14) |
|
k=1 |
|
k=1 |
|
ибо f (ξk) g(ξk), |
k = 1, 2, ..., kτ . Переходя в неравенстве (24.14) |
||
(24.11) |
|
|
|
к пределу при |τ | → 0, получим неравенство (24.12).
Неравенство (24.13) следует из неравенства (24.12) при g(x) ≡ 0.
8◦. Если функция f интегрируема и неотрицательна на отрезке [a, b], существует точка x0 [a, b], в которой функция f непрерывна, и f (x0) > 0, то
b
f (x) dx > 0.
a
Если функция f непрерывна в точке x0 [a, b] и f (x0) > 0, то из
очевидного неравенства f (x0) > f (x0) > 0 согласно «лемме о сохра-
2
нении знака» (см. следствие из следствия 2◦ в п. 6.7) следует, что
существует такой отрезок [α, β], что x0 [α, β] [a, b], α < β, и для всех точек x [α, β] выполняется неравенство
f (x) |
f (x0) |
, |
(24.15) |
|
|||
2 |
|
|
|

280 Гл. 2. Интегральное исчисление функций одной переменной
|
|
kτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если теперь στ (f ) = |
f (ξk)Δxk, ξk [xk−1, xk ], |
k = 1, 2, ..., kτ , |
|||||||||||
т. е. στ (f ) |
|
k=1 |
|
|
|
|
|
|
то |
|
|
|
|
— интегральная сумма Римана функции f , |
(24.18) |
||||||||||||
|στ (f )| = k=1 f (ξk)Δxk |
k=1 |f (ξk)| xk = στ (|f |), |
||||||||||||
|
kτ |
|
|
|
|
kτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где в правой части |
неравенства |
стоит интегральная сумма Римана |
|||||||||||
|
f . |
lim |
σ |
|
|
b |
lim σ |
|
( f ) = |
b |
|
dx, |
|
функции | |
|
(f ) = f (x) dx, |
|
f (x) |
| |
||||||||
| Так как τ 0 |
|
τ |
|
|
τ 0 |
τ |
| |
| |
| |
|
|||
|
|
| |→ |
|
|
|
a |
| |→ |
|
|
|
a |
|
|
то, перейдя в неравенстве (24.18) к пределу при |τ | → 0, получим |
|
||||||||||||
|
|
b f (x) dx b |f (x)| dx. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
Заметим, что если не предполагать, что a < b (см. п. 23.1), то вместо неравенства (24.16) следует писать
b |
|
b |
|f (x)| dx . |
(24.19) |
a f (x) dx |
a |
|||
|
|
|
|
|
|
|
|
|
|
10◦. Н е п р е р ы в н о с т ь и н т е г р а л а. Если функция f |
инте- |
|||
грируема на отрезке [a, b], то функции |
|
|||
|
|
x |
|
|
F (x) |
def |
f (t) dt, |
(24.20) |
|
= |
||||
|
|
a |
|
|
|
|
b |
|
|
G(x) |
def |
f (t) dt |
(24.21) |
|
= |
||||
x
непрерывны на этом отрезке.
С л е д с т в и е. Если функция f интегрируема на отрезке [a, b], то
b−ε b
lim |
f (x) dx = f (x) dx, 0 < ε < b |
− |
a. |
(24.22) |
ε 0 |
|
|
|
|
→ |
|
|
|
|
a+ε |
a |
|
|
|
Функция f , будучи интегрируемой на отрезке [a, b], ограничена на нем, поэтому существует такая постоянная c > 0, что для всех x [a, b] выполняется неравенство
|f (x)| c. |
(24.23) |
282 |
Гл. 2. Интегральное исчисление функций одной переменной |
|||||||
Для того чтобы убедиться в справедливости равенства (24.22), |
||||||||
выберем какую-либо точку c (a, b), тогда функции |
c |
x |
||||||
f (t) dt и f (t) dt |
||||||||
|
|
|
|
|
|
|
x |
c |
в силу свойства 9◦ непрерывны соответственно в точках x |
= a и x = b, |
|||||||
поэтому при 0 < ε < b − a будем иметь |
|
|
|
|||||
b−ε |
|
|
c |
b−ε |
|
c |
|
|
lim |
f (x) dx = |
lim |
f (x) dx + |
f (x) dx = lim |
f (x) dx + |
|||
ε→0 a+ε |
(24.3) ε→0 |
a+ε |
|
c |
! |
ε→0 a+ε |
||
|
b−ε |
|
|
c |
|
b |
b |
f (x) dx. |
|
+ lim |
f (x) dx = |
f (x) dx + |
f (x) dx |
= |
|||
|
ε 0 |
|
св. 9◦ |
|
|
|
(24.3) |
|
|
→ |
|
|
|
|
|
|
|
|
c |
|
|
a |
|
c |
a |
|
24.2. Интегральная теорема о среднем. |
|
|
||||||
Те о р е м а. Пусть на отрезке [a, b]: |
|
|
|
|||||
1) функции f и g интегрируемы; |
|
|
|
|
||||
2) m f (x) M ; |
|
|
|
|
|
(24.27) |
||
3) функция g не меняет знака. |
m μ M , |
что |
|
|||||
Тогда существует такое число μ, |
|
|||||||
|
|
b |
|
|
b |
|
|
|
|
|
|
f (x)g(x) dx = μ |
g(x) dx. |
|
(24.28) |
||
|
|
a |
|
|
a |
|
|
|
С л е д с т в и е. Если в дополнение к условиям теоремы функция f |
||||||||
|
|
|
|
непрерывна на отрезке [a, b], то на |
||||
|
|
|
|
интервале (a, b) существует такая |
||||
|
|
|
|
точка ξ, что |
|
|
||
|
|
|
|
b |
|
|
b |
|
|
|
|
|
f (x)g(x) dx = f (ξ) g(x) dx, |
||||
|
|
|
|
a |
|
|
a |
(24.22) |
|
|
|
|
|
|
a < ξ < b, |
||
|
|
|
|
|
|
|
||
|
|
|
|
в частности, при g(x) ≡ 1 на [a, b] |
||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
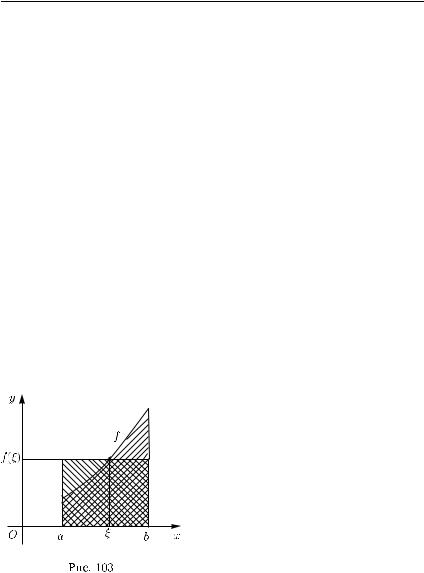
f (x) dx = f (ξ)(b − a), |
a < ξ < b |
|||
|
|
|
|
a |
|
|
|
|
|
|
|
|
(рис. 103). |
|
|
||
Умножив неравенство (24.27) на g(x), |
получим, что для всех x |
|||||||
[a, b] в случае g(x) 0 выполняется неравенство |
|
|
||||||
|
|
mg(x) f (x)g(x) M g(x), |
|
|
||||
а в случае g(x) 0 — неравенство
mg(x) f (x)g(x) M g(x).

284 Гл. 2. Интегральное исчисление функций одной переменной
b |
b |
тогда |
f (x)g(x) dx = μ g(x) dx, причем в силу (24.34) и (24.35) вы- |
a |
a |
полняется неравенство m μ M. |
|
Докажем следствие.
Если функция f непрерывна на отрезке [a, b], то согласно теореме Вейерштрасса она достигает своих наибольшего и наменьшего значений в некоторых точках α и β этого отрезка:
f (α) = min f (x), |
f (β) = max f (x). |
(24.36) |
[a,b] |
[a,b] |
|
При |
|
|
m = f (α), M = f (β) |
(24.37) |
|
выполняется условие (24.27) теоремы и, следовательно, существует такое число μ,
m μ M , |
(24.38) |
для которого выполняется равенство (24.28).
Всилу условий (24.37), (24.38), согласно теореме Больцано–Коши
опромежуточных значениях непрерывной функции, на отрезке [a, b]
существует точка ξ, для которой имеет место равенство f (ξ) = μ, а поэтому и равенство (24.29). Покажем, что, более того, точку ξ всегда можно выбрать так, что она будет лежать на интервале (a, b).
b |
b |
Если |
g(x) dx = 0, то из формулы (24.28) следует f (x)g(x) dx = 0, |
a |
a |
поэтому равенство (24.29) выполняется при любом выборе точки ξ
(a, b).
Пусть теперь
b
g(x) dx = 0, |
(24.39) |
a
и для определенности g(x) 0 во всех точках x отрезка [a, b], а сле-
довательно,
b
g(x) dx 0. |
(24.40) |
a
(Случай g(x) 0, a x b, сводится к рассматриваемому заменой функции g(x) на функцию −g(x): применив к неотрицательной функции g(x) формулу (24.29) и умножив обе части равенства на −1, получим и в этом случае формулу (24.29).)
§ 24. Свойства интегрируемых функций |
285 |
Из выполнения условий (24.39) и (24.40) следует, что
b
g(x) dx > 0. |
(24.41) |
a
Всилу неравенства (24.38) возможны три случая: m < μ < M ,
μ= M и μ = m. Если m < μ < M , то из условий (24.37) согласно тео-
реме Больцано–Коши о промежуточных значениях непрерывной на
отрезке функции следует, что между точками α и β, а следовательно, на интервале (a, b) существует такая точка ξ, что f (ξ) = μ.
Если же μ = M , то равенство (24.28) примет вид
b |
b |
|
|
f (x)g(x) dx = M g(x) dx, |
|
a |
a |
|
откуда |
b |
|
|
|
|
|
(M − f (x))g(x) dx = 0. |
(24.42) |
a
Из неравенства (24.41) в силу следствия из свойства 10◦ определенного интеграла (см. п. 24.1) существует такое ε > 0, что
b−ε
g(x) dx > 0. |
(24.43) |
a+ε
Если бы на интервале (a, b) не существовала точка ξ, в которой f (ξ) = M , то непрерывная функция M − f (x) была бы положительной во всех точках отрезка [a + ε, b − ε], а следовательно, и в точке x0[a + ε, b − ε], в которой она принимает наименьшее значение на этом отрезке; т. е., если
M |
− |
f (x |
0) = |
min |
, |
24 44 |
|
|
|
[a+ε,b ε](M − f (x)) |
|
( . |
) |
||
то |
|
|
|
− |
|
|
|
|
|
M − f (x0) > 0. |
|
(24.45) |
|||
Поэтому |
|
|
|
||||
|
|
|
|
|
|
|
|
b |
b−ε |
|
|
|
|
|
|
(M − f (x))g(x) dx (M − f (x))g(x) dx (24.44) |
|
|
|
||||
a |
a+ε |
|
|
b−ε |
|
|
|
|
|
|
|
|
g(x) dx (24.43) |
|
|
|
|
|
|
(24.44)(M − f (x0)) |
0, |
||
|
|
|
|
|
|
> |
|
|
|
|
|
|
a+ε |
(24.45) |
|

