
Краткий курс математического анализа. Том 1
.pdf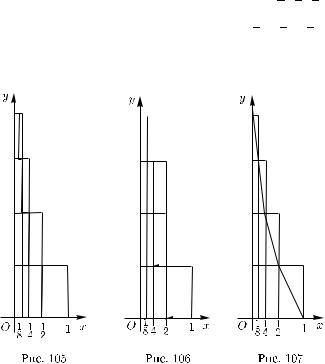
§ 27. Площади и объемы |
297 |
прямоугольникам, лежащим в квадрате, площади которых образуют бесконечно убывающую геометрическую прогрессию 12 , 14 , 18 , ..., сум-
ма которой равна 1, т. е. площади квадрата Q: 12 + 14 + 18 + ... = 1.
Естественно, что площадь бесконечной фигуры P равна (как это можно доказать) площади квадрата Q, т. е. положительной конечной величине.
Заметим, что бесконечная фигура P лежит над осью x и под графиком «ступенчатой» (кусочно-постоянной) функции, изображенной на рис. 106.
Нетрудно получить и бесконечное множество конечной площади, ограниченное графиком непрерывной на полуинтервале (0, 1] функции, положительной полуосью оси y, отрезком 0 x 1, y = 0, оси x. Чтобы получить график такой функции, достаточно, например, соединить прямолинейными отрезками правые концы ступенек графика функции, изображенной на рис. 106. В результате получится функция, график которой изображен на рис. 107.
Отметим, что эта функция, будучи неограниченной, неинтегрируема по Риману.
27.3. Понятие объема. Пусть в трехмерном пространстве R3 фиксирована декартова прямоугольная система координат x, y, z. Аналогично разбиению плоскости на квадраты ранга k = 0, 1, 2, ...
можно произвести разбиение пространства R3 на кубы с помощью плоскостей, параллельных координатным плоскостям и отстоящих

§ 28. Приложения определенного интеграла |
299 |
Множество вида (28.1) называется криволинейной трапецией, порожденной графиком функции f (рис. 108).
Пусть τ = {xk }kk==0kτ — разбиение отрезка [a, b], |
|
|
||
k = [xk−1, xk ], xk |
= xk − xk−1 |
, mk = xinfk f (x), |
Mk = sup f (x), |
|
|
|
|
x |
k |
|
|
|
|
|
|
|
k = 1, 2, ..., kτ . |
(28.3) |
|
Обозначим соответственно через pτ и Pτ замкнутые прямоугольники, составленные из всех прямоугольников вида
pτ ,k = {(x, y) : xk−1 |
x xk, |
0 |
y mk}, |
(28.4) |
|
Pτ ,k = {(x, y) : xk−1 |
x xk, |
0 |
y Mk }, |
(28.5) |
|
т. е. |
|
|
|
|
|
k |
|
|
|
|
|
pτ = kτ |
pτ ,k, Pτ = kτ |
Pτ ,k. |
(28.6) |
||
=1 |
|
k=1 |
|
|
|
Из (28.3) следует, что для любого разбиения τ выполняется включение pτ P Pτ , а следовательно (см. теорему в п. 27.1),
μpτ μP μPτ . |
(28.7) |
Из (28.4) и (28.5) следует, что μpτ ,k = mk |
xk , μPτ ,k = Mk xk , и так |
как прямоугольники Pτ ,k, соответственно pτ ,k, не имеют общих внутренних точек, то в силу (28.6)
|
kτ |
kτ |
|
μpτ = μpτ ,k = mk |
xk = sτ , |
||
|
k=1 |
k=1 |
(28.8) |
|
|
|
|
|
kτ |
kτ |
|
|
|
|
|
μPτ = |
μPτ ,k = |
Mk |
xk = Sτ . |
|
k=1 |
k=1 |
|

302 Гл. 2. Интегральное исчисление функций одной переменной
Pτ ,k = {(ρ, ϕ) : ϕk−1 ϕ ϕk , |
|
0 ρ Mk }, |
|
k |
k = 1, 2, ..., kτ , |
|
|
pτ = kτ |
pτ ,k, Pτ = kτ |
Pτ ,k. |
|
=1 |
|
k=1 |
|
Множества pτ ,k и Pτ ,k представляют собой круговые секторы с углом ϕk и радиусами соответственно mk и Mk , а pτ и Pτ — ступенчатые фигуры, составленные из указанных секторов и соответственно содержащиеся в множестве P и содержащие его: pτ P Pτ . Из этих
включений следует, что |
|
μpτ μP μPτ . |
(28.14) |
Согласно формуле для площади сектора
|
μpk,τ = |
1 |
mk2 |
ϕk, |
μPk,τ = |
1 |
|
Mk2 |
ϕk, |
|
|
|
|||
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μpτ = kτ |
μpk,τ = |
1 |
kτ |
mk2 |
ϕk , |
μPτ = kτ |
μPk,τ = |
1 |
kτ |
Mk2 |
ϕk . |
||||
|
|
|
|
||||||||||||
k=1 |
2 |
k=1 |
|
|
|
k=1 |
2 |
k=1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получившиеся суммы являются соответственно нижней sτ и верх- |
|
ней Sτ суммами Дарбу функции 1 ρ2(ϕ) : sτ = μpτ , Sτ = μPτ . Таким |
|
2 |
|
образом, в силу (28.14) |
|
sτ S = μP Sτ . |
(28.15) |
Поскольку суммы Дарбу sτ и Sτ |
при |τ | →10 стремятся к одному |
||||||||||
и тому же пределу — интегралу от функции |
|
ρ2 |
(ϕ): |
||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
β |
|
|
|
|
lim sτ |
= lim Sτ |
= |
1 |
ρ2(ϕ) dϕ, |
|||||||
|
|||||||||||
|τ |→0 |
|τ |→0 |
|
2 |
|
|
|
|
||||
|
|
|
α |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
то из неравенств (28.15) следует, что |
|
|
|
|
|||||||
|
|
|
β |
|
|
|
|
|
|
|
|
|
S = |
1 |
|
ρ2(ϕ) dϕ. |
|
|
(28.16) |
||||
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
α |
|
|
|
|
|
|
|
|
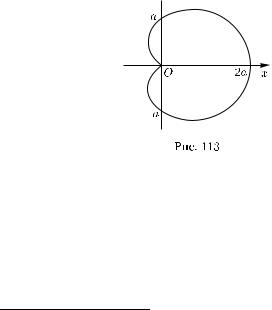
П р и м е р. Найдем площадь S множества, ограниченного кривой |
|||||||||||
ρ = a(1 + cos ϕ), |
0 ϕ 2π |
|
|||||||||
§ 28. Приложения определенного интеграла |
303 |
(она называется кардиоидой; рис. 113): |
|
|
|
|
|
|||||||
S = |
a2 |
2π(1 + cos ϕ)2 dϕ = |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2π |
|
2π cos ϕ dϕ + |
|
2π |
|
|
|
|
||
|
|
= |
a2 |
dϕ + a2 |
a2 |
1 + cos 2ϕ |
dϕ = |
3 |
πa2. |
|||
|
|
|
|
|
|
2 |
|
|||||
2 |
|
|
2 |
|
2 |
|
||||||
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
28.3. Вычисление длины кривой. Применение определенного интеграла к задачам вычисления площадей множеств было основано на его равенстве пределу интегральных сумм. Приведем теперь пример приме- 
нения определенного интеграла, который основан на формуле Ньютона–Лейбница, позволяющий найти значение функции,
если известна ее производная. Пусть Γ — кривая, заданная своим
непрерывно дифференцируемым векторным представлением r = r(t), a t b; тогда она спрямляема, и если s = s(t) — ее переменная длина дуги, отсчитываемая
от начала, то функция s(t) дифференцируема и s (t) = |r (t)|.
По формуле Ньютона–Лейбница для длины S = s(b) кривой имеем формулу
b |
b |
|
S = s(b) − s(a) = s (t) dt = |r (t)| dt (s(a) = 0). |
(28.17) |
|
a |
a |
|
Если r(t) = (x(t), y(t), z(t)), то
b
S = |
[x (t)]2 + [y (t)]2 + [z (t)]2 dt. |
(28.18) |
a
В случае, когда кривая Γ является графиком функции y = f (x), a x b, для ее длины S в силу (28.18) справедлива формула
S = b |
|
dx. |
(28.19) |
1 + y 2 |
|||
a |
|
||
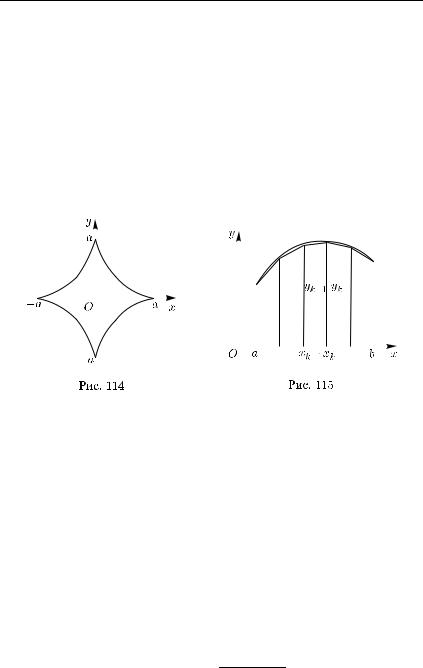
П р и м е р. Вычислим длину астроиды
x = a cos3 t, y = a sin3 t
304 Гл. 2. Интегральное исчисление функций одной переменной
(рис. 114). В силу симметричности астроиды относительно координатных осей ее длина S равна учетверенной длине ее части, лежащей в первом координатном угле, т. е. соответствующей изменению параметра на отрезке [0, π/2].
Заметив, что
x = −3a cos2 t sin t, y = 3a sin2 t cos t,
согласно формуле (28.18), в которой надо положить z = 0, получим
|
|
π/2 |
|
|
|
|
|
|
|
|
π/2 |
|
|
|
S = 4 |
0 |
9a2 cos4 t sin2 t + 9a2 sin4 t cos2 t |
dt = 6a |
0 |
sin 2t dt = 6a. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28.4. Площадь поверхности вращения. Пусть на отрезке
[a, b] задана неотрицательная функция y = f (x): f (x) 0, a x b.
Множество, получающееся вращением графика функции f (x) вокруг оси Ox, называется поверхностью вращения (этого графика).
Определим ее площадь. Пусть τ = {xk }kk==k0τ — какое-либо разбиение отрезка [a, b]. Впишем в график функции f ломаную λτ , соответствующую разбиению τ , т. е. ломаную с вершинами в точках (xk, yk ),
где |
|
|
yk = f (xk), |
k = 0, 1, ..., kτ |
(28.20) |
(рис. 115). Звено этой ломаной |
с концами в точках |
(xk−1, yk−1) |
и (xk, yk ) (будем называть его k-м звеном ломаной λτ ) при вращении
его вокруг оси x описывает боковую поверхность усеченного конуса (в частности, при yk−1 = yk — боковую поверхность цилиндра, а при yk−1 = 0 или yk = 0 — боковую поверхность конуса), площадь которой равна
π(yk−1 + yk ) x2k + yk2 , (28.21)

§ 28. Приложения определенного интеграла |
305 |
где yk−1 и yk — соответственно радиусы оснований усеченного ко-
нуса, а |
xk2 + |
yk2 — длина его образующей, xk = xk − xk−1, |
|||
− |
|
− |
|
, |
k = 1, 2, ..., kτ . Поэтому площадь Lτ поверхности, |
yk = yk yk |
|
1 |
|||
получающейся от вращения ломаной λτ вокруг оси Ox, выражается формулой
kτ |
+ yk ) xk2 |
|
|
|
|
|
|
Lτ = π k=1(yk−1 |
+ yk2 . |
(28.22) |
Если существует предел lim Lτ , то он называется площадью по-
|τ |→0
верхности вращения, образованной вращением графика функции вокруг оси x. Таким образом, обозначив через L площадь указанной поверхности вращения, будем иметь
def |
(28.23) |
L = lim Lτ . |
|
|τ |→0 |
|
Пусть теперь функция f непрерывно дифференцируема на отрезке [a, b]; тогда для площади поверхности L можно получить удобную для вычислений формулу в виде некоторого интеграла.
Те о р е м а 2. Если функция f непрерывно дифференцируема и неотрицательна на отрезке [a, b], то для площади поверхности вращения, образованной вращением графика функции f вокруг оси Ox, имеет место формула
L = 2π f (x) 1 + f 2(x) dx.
a
Функция f непрерывно дифференцируема на отрезке [a, b], т. е. ее производная непрерывна, и, следовательно, ограничена на этом отрезке. Это означает, что существует такая постоянная c > 0, что для всех точек x [a, b] выполняется неравенство
|
|
|
|
|f (x)| c. |
|
|
|
(28.24) |
||
По формуле конечных приращений Лагранжа имеем |
|
|
||||||||
yk = yk − yk−1 = f (ξk)Δxk, xk−1 < ξk < xk, |
k = 1, 2, ..., kτ . |
|
||||||||
Поэтому |
|
|
= |
|
xk, откуда |
|
|
|
||
xk2 + |
yk2 |
|
|
|
||||||
1 + f 2(ξk) |
|
|
|
|||||||
|
|
|
kτ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
L |
= |
π k=1(yk−1 + yk ) |
1 + |
2 |
|
28 25 |
|
||
|
τ (28.22) |
|
f (ξk) |
xk . |
( . |
) |
||||

