
Краткий курс математического анализа. Том 1
.pdf

348 Гл. 3. Ряды
Те о р е м а 7 (признак Даламбера). Пусть для ряда
∞ |
|
|
|
|
|
|
|
n = 1, 2, ..., |
(30.27) |
un, |
un > 0, |
|||
n=1 |
|
|
|
|
существует предел |
lim |
un |
= l. |
(30.28) |
|
||||
|
|
|||
|
n→∞ un−1 |
|
|
|
Тогда если l < 1, то ряд (30.27) сходится, а если |
l > 1, то |
|||
расходится. |
|
|
|
|
Пусть сначала l < 1. |
Выберем число q так, чтобы |
l < q < 1. |
||
Тогда в силу условия (30.28) существует такой номер n0 > 1, что |
||
для всех n > n0 выполняется неравенство |
un |
< q и, следовательно, |
u |
||
|
n−1 |
|
неравенство un < qun−1. Применяя это неравенство последовательно для n = n0 + 1, n0 + 2, ..., получим
un0+1 < qun0 ,
un0+2 < qun0+1 < q2un0 ,
. . . . . . . . . . .
un0+k < qk un0 ,
. . . . . . . . . . .
∞ |
∞ |
|
∞ |
|
|
|
|
Но ряд |
qk un0 = un0 |
qk в силу условия 0 < q < 1 сходит- |
|
k=1 |
k=1 |
|
|
ся, поэтому, согласно признаку сравнения, сходится и ряд |
un0+k , |
||
а следовательно, и ряд (30.27). |
|
k=1 |
|
|
|
||
Пусть теперь l > 1; тогда в силу условия (30.28) существует такой
номер n0, что для всех n > n0 выполняется неравенство un > 1,
un−1
а поэтому и неравенство un > un−1. Применяя его последовательно для n = n0 + 1, n0 + 2, ..., получим
un+1 > un > ... > un0+1 > un0 > 0.
Поэтому последовательность членов ряда (30.27) не стремится к нулю, откуда и следует его расходимость.
Те о р е м а 8 (признак Коши). Пусть для ряда
∞ |
|
|
|
|
|
|
|
|
|
0, |
(30.29) |
un, un |
|||||
n=1 |
|
|
|
|
|
существует предел |
√un = l. |
(30.30) |
|||
lim |
|||||
|
n |
|
|
|
|
n→∞ |
|
|
|||
Тогда если l < 1, то ряд |
(30.29) |
сходится, а если |
l > 1, то |
||
расходится. |
|
|
|
|
|

§ 30. Числовые ряды |
349 |
Пусть сначала l < 1. Выберем число q так, чтобы l < q < 1. Тогда в силу условия (30.30) существует такой номер n0, что для всех
|
|
|
|
|
n |
|
n |
|
|
||
n > n0 выполняется неравенство √un |
< q и, следовательно, un < q . |
||||
|
∞ |
|
∞ |
|
|
Поскольку ряд |
|
|
|
|
|
qn сходится, то сходится ряд |
un0+k, а поэтому |
||||
|
n=0 |
|
k=1 |
|
|
и ряд (30.29).
Если l > 1, то в силу условия (30.30) существует такой номер n0,
√
что при n > n0 выполняется неравенство n un > 1, т. е. un > 1, и, следовательно, последовательность членов ряда (30.29) не стремится к нулю, поэтому этот ряд расходится.
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
П р и м е р ы. 3. Ряд |
|
|
|
|
сходится. Это устанавливается, напри- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n=1 |
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мер, с помощью признака Даламбера: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
1/n! |
|
|
|
|
|
|
= lim |
1 |
|
= 0. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
n→∞ 1/(n − 1)! |
|
|
|
|
n→∞ n |
|
|
|
|
|
|
|||||||||||||||||||||
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сходится. Это сразу можно установить с помощью |
|||||||||||||||||||||||||||||||||
4. Ряд |
|
|
|||||||||||||||||||||||||||||||||||
n=1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
признака Коши: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
lim |
n |
|
1 |
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
n→∞ |
= n→∞ n |
= . |
|
|
|
|
|||||||||||||||||||||||||
5. Для ряда с общим членом un = |
1 |
, |
|
α > 0, |
имеем |
||||||||||||||||||||||||||||||||
α |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
un+1 |
|
= lim |
|
|
|
|
nα |
|
|
|
= |
|
|
lim |
|
n |
|
α = 1, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n→∞ |
|
un |
|
|
n→∞ (n + 1)α |
|
|
n→∞ n + 1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
lim √un = lim |
|
|
|
|
= |
|
|
|
|
|
|
α = 1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
n |
|||||||||||||||||||||
|
|
|
|
n |
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
||||||||||
n→∞ |
|
|
|
n |
|
|
|
|
|
(nlim |
|
n |
) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
||||||
(см. пример 4 в п. 13.2). Таким образом, при применении признаков Даламбера и Коши соответствующие пределы равны единице, т. е. при помощи этих признаков нельзя определить, сходятся или расходятся рассматриваемые ряды. Среди них есть как сходящиеся при α > 1,
так и расходящиеся при α 1. Иначе говоря, среди рядов |
∞ |
|
||||||||||
|
un |
|||||||||||
|
|
|
|
|
|
|
un+1 |
n=1 |
|
|||
|
|
|
|
|
|
|
|
|
||||
с неотрицательными членами, для которых lim |
|
= 1, соответ- |
||||||||||
un |
||||||||||||
|
|
|
|
|
|
n→∞ |
∞ |
|
1 |
|
||
|
|
|
|
∞ 1 |
|
|
|
|||||
lim |
n u |
= 1, |
|
|
|
, |
||||||
ственно n→∞ |
√ n |
|
имеются как сходящиеся например, n=1 n2 |
|
||||||||
|
|
|
|
|
|
ряды. |
|
|
|
|
|
|
так и расходящиеся например, n=1 |
n |
|
|
|
|
|
||||||
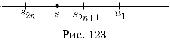
350 |
Гл. 3. Ряды |
30.5. Знакочередующиеся ряды.
Те о р е м а 9 (Лейбниц). Если последовательность {un} убывает
истремится к нулю, т. е.
un un+1, |
n = 1, 2, ..., lim un = 0, |
(30.31) |
||
то ряд |
|
n→∞ |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
(−1)n+1un |
|
(30.32) |
|
|
n=1 |
|
|
|
|
∞ |
|
n |
|
|
|
(−1)n+1un, sn = |
|
(−1)k+1uk , то |
сходится, причем, если |
s = |
|
||
|
n=1 |
|
k=1 |
|
при любом n = 1, 2, ... выполняется неравенство |
|
|
||
|
|sn − s| un+1. |
|
(30.33) |
|
Прежде всего отметим, что из условия (30.31) следует, что |
||||
|
un 0, |
|
(30.34) |
|
в силу чего члены ряда (30.32) поочередно то 0, то 0.
Ряды вида (30.32) при un > 0 называются знакочередующимися.
Частичные суммы с четными номерами ряда (30.32) возрастают и неотрицательны. В самом деле,
s2n+2 = (u1 − u2) + (u3 − u4) + ... + (u2n+1 − u2n+2) =
= s2n + (u2n+1 − u2n+2) s2n 0, n = 2, 3, ..., (30.35)
ибо в силу убывания последовательности {un} значения всех выражений, стоящих в круглых скобках, неотрицательны. Кроме того, последовательность {s2n} ограничена сверху:
s2n = u1 − (u2 − u3) − ... − (u2n−2 − u2n−1) − u2n u1, (30.36)
ибо |
0, k = 1, 2, ..., u2n(30.34)0. |
uk − uk+1 |
Поскольку последовательность {s2n} возрастает и ограничена сверху, то она имеет конечный предел
s = lim s2n, |
(30.37) |
n→∞ |
|
при этом из неравенств (30.35) и (30.36) следует, что (рис. 123) |
|
0 s u1. |
(30.38) |
Покажем, что тот же предел имеет и последовательность частичных сумм с нечетными номерами. Действительно,
s2n+1 = s2n + u2n+1,

§ 30. Числовые ряды |
351 |
|
lim u2n+1 |
= 0, |
|
|
|
n→∞ |
(30.31) |
|
|
поэтому |
|
|
|
|
lim s2n+1 |
= lim s2n + lim u2n+1 |
= s. |
(30.39) |
|
n→∞ |
n→∞ |
n→∞ |
(30.37) |
|
Из (30.37), (30.39) следует, что последовательность {sn} всех частичных сумм ряда (30.32) имеет конечный предел s, т. е. этот ряд сходится, и s является его суммой.
Докажем неравенство (30.33). Имеем
s − sn = ∞ (−1)n+k+1un+k = (−1)n ∞ (−1)k+1un+k ,
k=1 |
k=1 |
где в правой части стоит ряд ∞ (−1)k+1un+k . Применив к нему нера-
k=1
венство (30.38), получим
0 ∞ (−1)k+1un+k un+1, k=1
поэтому
|s − sn| = ∞ (−1)k+1un+k un+1.
k=1
|
|
|
|
П р и м е р. Ряд |
∞ |
(−1)n |
сходится. Это сразу следует из теоре- |
|
|
n |
|
мы 9. |
n=1 |
|
|
|
|
|
|
З а м е ч а н и е. Выше (см. следствие теоремы 6 в п. 30.4) было
∞ ∞
показано, что если у двух знакопостоянных рядов |
un и |
vn |
n=1 n=1
их члены эквивалентны: un vn, n → ∞ (см. (30.22)), то они одновременно сходятся или расходятся. Для не знакопостоянных рядов аналогичное утверждение уже не имеет места. Например, если
u |
|
= |
(−1)n |
, |
v = |
(−1)n + |
1 |
, |
|||||||
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
|
√n |
n |
√n |
|
|
||||||
то |
|
|
vn |
= n→∞ |
( 1)n |
= |
|
||||||||
|
|
|
|
||||||||||||
|
−√n |
|
|||||||||||||
n→∞ |
un |
|
|||||||||||||
lim |
|
|
|
|
|
lim |
1 + |
|
|
|
|
|
1, |
||

352 Гл. 3. Ряды
u |
v , n |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
∞ |
(−1)n |
|
|
∞ |
|
1)n |
1 |
|
|
|
|||||||||||||
т. е. |
n n |
→ ∞ |
|
|
Однако в силу признака Лейбница ряд |
√n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
||
сходится, а ряд n=1 |
(−√ |
|
|
+ |
|
|
|
расходится, ибо расходится гармони- |
||||||||||||
n |
||||||||||||||||||||
n |
||||||||||||||||||||
|
∞ |
|
1 |
|
1 |
|
|
|
|
|
( 1)n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ческий ряд |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n=1 |
n |
|
|
|
= o |
|
|
|
|
|
, |
|
|
||||||
|
|
|
|
|
−√ |
|
|
|
|
|
|
|||||||||
Очевидно, что |
|
|
|
n → ∞. Таким образом, добавляя |
||||||||||||||||
n |
||||||||||||||||||||
n |
||||||||||||||||||||
к членам ряда бесконечно малые более высокого порядка по сравнению с членами ряда, можно изменить сходимость ряда: из сходящегося ряда получить расходящийся.
30.6. Абсолютно сходящиеся ряды.
О п р е д е л е н и е 3. Ряд
∞ |
|
|
(30.40) |
un, un C, |
n=1
называется абсолютно сходящимся, если ряд, членами которого являются абсолютные величины членов данного ряда, т. е.
∞ |
|
|
(30.41) |
|un|, |
n=1
сходится.
Те о р е м а 10 (критерий Коши абсолютной сходимости ряда). Для того чтобы ряд (30.40) абсолютно сходился, необходимо и достаточно, чтобы для любого ε > 0 существовало такое n0, что для всех номеров n > n0 и всех p = 0, 1, ... выполнялось бы неравенство
p
|un+k | < ε.
k=0
Это сразу следует из определения абсолютно сходящегося ряда и критерия Коши сходимости ряда (теорема 4 из п. 30.3).
Те о р е м а 11. Если ряд абсолютно сходится, то он сходится.
Это следует из неравенства
p |
|
p |
|
|
|
(30.42) |
|
k=0 un+k |
|
k=0 |un+k |. |
|
|
|
|
|
В самом деле, в силу критерия Коши абсолютной сходимости ряда (30.40) для любого ε > 0 существует такое n0, что для всех n > n0 и всех p 0 правая часть неравенства (30.42) меньше ε. Следовательно, и левая часть этого неравенства окажется меньше ε, т. е. для ряда

354 Гл. 3. Ряды
Зафиксируем произвольно ε > 0. В силу абсолютной сходимости ряда (30.40) существует такой номер n0, что
|
|
∞ |
|
|
ε |
|
|
|
|
|
|
|un| = s − sn0 < |
|
|
|
(30.44) |
|||
|
|
2 |
|||||||
|
|
n +1 |
|
|
|
|
|
|
|
|
n= 0 |
неравенство |
|
||||||
и, следовательно, выполняется |
$ |
$ |
|
|
|
|
|
||
|
|
∞ |
|
∞ |
|
||||
|s − sn0 |
| = |
|
|
|
|
|
|
(30.45) |
|
n=n0+1 un n=n0+1 |un| < 2ε . |
|||||||||
|
|
|
|
|
|
|
|
|
|
Выберем номер m0 так, чтобы частичная сумма sm0 ряда (30.43) содержала в качестве своих слагаемых все члены ряда (30.40), входящие в сумму sn0 . Для всякого m > m0 положим
sm = sm − sn0 . |
(30.46) |
В силу выбора номера m0 слагаемыми суммы sm0 являются члены ряда (30.40) с номерами, большими n0. Поскольку абсолютная величина суммы sm не превышает абсолютных величин ее слагаемых, то
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
ε |
|
|
|
|
|
|
|
||
|
|
|
s |
| |
|
u |
|
< |
|
|
. |
|
|
|
|
|
(30.47) |
|
|
|
|
| |
m |
|
| n| (30.44) |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
=n +1 |
|
|
|
|
|
|
|
|
|
|
|
||
Поэтому при m > m0 будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|||||||
s |
s |
= s |
(s |
|
+ s ) |
|
s |
s |
n0 | |
+ s |
| |
< |
ε |
+ |
ε |
= ε. |
||
|
|
2 |
2 |
|||||||||||||||
| − |
m| |
(30.46) | − |
|
n0 |
m |
| | − |
|
| m |
(30.45) |
|
|
|||||||
|
|
lim s = s. |
|
|
|
|
|
|
|
(30.47) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Это означает, что m→∞ |
m |
|
Иначе говоря, ряд (30.43) сходится |
|||||||||||||||
и его сумма равна s, |
т. е. равна сумме ряда (30.40): |
|
|
|
|
|||||||||||||
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
um |
= s = |
|
un. |
|
|
|
|
|
|
|
|
||
|
|
|
|
m=1 |
|
n=1 |
|
|
|
|
|
|
|
|
|
|||
Второе утверждение — абсолютная сходимость ряда (30.43) — следует из уже доказанного первого утверждения, если его применить
к ряду
∞
|un|. (30.48)
n=1
В самом деле, если ряд (30.40) абсолютно сходится, то сходится ряд (30.48), причем он, очевидно, сходится абсолютно, так как его члены неотрицательны. Поэтому согласно доказанному сходится и любой ряд, получающийся перестановкой членов ряда (30.48), в частности,
|
∞ |
|um|. А это и означает, что ряд |
∞ |
сходится ряд |
|
um абсолютно |
|
сходится. |
m=1 |
|
m=1 |
|
|
|


