Краткий курс математического анализа. Том 1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Отметим, что последовательность

Отметим, что последовательность

членов гармонического ря-

да стремится к нулю:

членов гармонического ря-

.pdf

Скачиваний:

776

Добавлен:

10.05.2015

Размер:

5.57 Mб

Скачать

☆

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 4535 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

§ 29. Несобственные интегралы

337

Подобным же образом вводится и понятие неопределенного инте-

грала от функции (29.50):
f (x) dx = u(x) dx + i v(x) dx.	(29.52)

Для этого интеграла также имеет место свойство линейности, справедливы формулы замены переменной и интегрирования по частям, которые в силу формулы (29.52) вытекают из соответствующих свойств интегралов от функций действительного аргумента, принимающих только действительные значения.

Для непрерывных функций f определенный и неопределенный интегралы (29.51) и (29.52), как и в действительной области, связаны

соотношением	x
	f (x) dx = f (t) dt + C.
	a

Г л а в а 3

РЯДЫ

§30. Числовые ряды

30.1.Определение ряда.

О п р е д е л е н и е 1. Пара последовательностей {un} и {sn}, где un, sn C, n = 1, 2, ...,

	sn = u1 + u2 + ... + un, n = 1, 2, ...,	(30.1)
называется рядом (а также бесконечной суммой) и обозначается
	u1 + u2 + ... + un + ...
или	∞
		(30.2)
	un.	(30.2)

n=1

Элементы последовательности {un} называются членами ряда, а элементы последовательности {sn} — его частичными суммами.

Если существует конечный предел

lim sn = s,	(30.3)
n→∞

то он называется суммой ряда. В этом случае ряд называется сходя-

щимся и пишут

∞

un = s.

n=1

Если последовательность частичных сумм {sn} не стремится к конечному пределу, то ряд (30.2) называется расходящимся.

Очевидно, что

u1 = s1, un = sn − sn−1, n = 2, 3, ...

(30.4)

Из формул (30.1) и (30.4) видно, что каждая из последовательностей {un} и {sn} однозначно определяет другую. Таким образом, чтобы задать ряд (30.2), достаточно задать одну из последовательностей {un} или {sn}. В этом смысле изучение рядов равносильно изучению последовательностей.

§ 30. Числовые ряды

339

Часто нумерацию членов ряда производят не натуральными числами, а целыми, начиная с нуля, т. е. числами 0, 1, 2, ..., а иногда — начиная с некоторого целого n0, т. е. числами n0, n0 + 1, ...

П р и м е р ы. 1. Примером сходящегося ряда является ряд

∞

qn,

(30.5)

n=0

членами

которого являются элементы геометрической прогрессии

{qn}, q C, |q| < 1. В самом деле, в этом случае

−

sn def=

1 − qn−1

n = 0, 1, 2, ...,

k=0

и потому

→∞

−

→∞

− −

−

→∞

lim sn =

lim

1 − qn+1

= lim

qn+1

1 q

= 1

−

nlim qn =

−

→∞

Следовательно, ряд (30.5) при |q| < 1 сходится и

∞

−

qn =

n=0

2. Примером расходящегося ряда является ряд, все члены которого

равны единице: un = 1,

поэтому

	n
n = 1, 2, ... В этом случае sn =		= n,
n = 1, 2, ... В этом случае sn =	1	= n,
nlim sn = +∞.	k=1
nlim sn = +∞.
→∞

30.2. Свойства сходящихся рядов.

Те о р е м а 1 (необходимые условия сходимости ряда). Если ряд сходится, то последовательность его членов стремится к нулю.

	∞

Если ряд		un сходится,	т. е.	существует конечный предел
lim	n=1
lim	sn = s его частичных сумм, то из равенства
n→∞		un = sn − sn−1,		n = 2, 3, ...,
следует, что		un = sn − sn−1,		n = 2, 3, ...,
следует, что
	nlim un = nlim sn − nlim sn−1 = s − s = 0.
	→∞	→∞	→∞

П р и м е р. Ряд (30.5), членами которого являются члены геометрической прогрессии {qn}, в случае, когда знаменатель прогрессии q по абсолютной величине не менее единицы, т. е. |q| 1, q C,

340	Гл. 3. Ряды

расходится, так как последовательность его членов {qn} не стремится

кнулю, ибо |qn| 1.

Те о р е м а 2. Если ряды ∞ un и ∞ vn сходятся, то для любых

			∞	n=1	n=1
			∞
λ C,	μ C ряд
λ C,	μ C ряд		λun + μvn сходится и
			n=1
			∞		∞	∞

			λun + μvn = λ		un + μ		vn.
			n=1		n=1	n=1
			n	n

Положим sn =				uk, σn =	vk , тогда
			k=1	k=1
				n

				λuk + μvk	= λsn + μσn.
			k=1
		∞		∞

Если ряды			un и	vn сходятся, т. е. существуют конечные пре-
	n=1			n=1	∞
делы lim sn =		∞		и lim σn =	∞	то существует и конечный
делы lim sn =			un	и lim σn =	vn,	то существует и конечный
n→∞		n=1		n→∞	n=1
предел
	n						∞	∞

lim	λuk + μvk = λ lim sn + μ lim					σn = λ	un + μ	vn,
n→∞ k=1				n→∞	n→∞		n=1	n=1
что и означает справедливость утверждения теоремы.
					∞

О п р е д е л е н и е 2. Для ряда					un ряд

n=1

∞

un+k

k=1

называется n-м остатком данного ряда.

Если n-й остаток ряда сходится, то его сумму будем обозна-

чать rn, т. е.	∞
rn =	un+k .	(30.6)

k=1

Те о р е м а 3. Если ряд сходится, то и любой его остаток сходится. Если какой-то остаток ряда сходится, то сам ряд также сходится, причем, если

∞		n	∞

s =	un, sn =	uk , rn =	un+k ,
n=1		k=1	k=1

(30.7) n→∞

§ 30. Числовые ряды	341
то при любом n = 1, 2, ...
s = sn + rn.	(30.7)

(n)

Пусть sn и sm являются соответственно n-й частичной суммой

∞

ряда un и m-й частичной суммой его остатка (30.6):

n=1
	sn = u1 + u2 + ... + un, sm(n) = un+1 + un+2 + ... + un+m;
тогда	sn+m = sn + sm(n).		(30.8)

Поэтому при произвольно фиксированном n пределы		lim sn+m
и lim		m→∞
	sm(n) одновременно существуют или не существуют. Существо-
m→∞			∞
вание	первого из этих пределов означает сходимость ряда		uk ,
	∞		k=1

а существование второго — сходимость остатка (30.6)		un+k этого
	k=1

ряда. Если оба рассматриваемых предела существуют, то, перейдя

к пределу при m → ∞ в равенстве (30.8), получим формулу (30.7).

∞

Отметим, что если ряд un сходится, то его остатки стремятся

n=1

к нулю. Это сразу следует из формулы (30.7), так как сходимость ряда

означает, что lim sn = s, и поэтому

n→∞

lim rn = lim (s − sn) = 0.

n→∞

30.3. Критерий Коши.

Те о р е м а 4 (критерий Коши сходимости ряда). Для того чтобы

	∞
		сходился, необходимо и достаточно, чтобы для любого
ряд	un
n=1			и всех целых
ε > 0	существовало такое n0, что для всех n > n0
p 0 имеет место неравенство
		\|un + un+1 + ... + un+p\| < ε.	(30.9)

Это утверждение сразу следует из критерия Коши существования конечного предела последовательности, примененного к последовательности частичных сумм {sn} данного ряда, ибо

un + un+1 + ... + un+p = sn+p − sn−1.

342	Гл. 3. Ряды
		∞
	З а м е ч а н и е. При p = 0 из теоремы следует, что если ряд
		un
		n=1
сходится, то для любого ε > 0 существует такой номер n0, что для

всех n > n0 выполняется неравенство \|un\| < ε, а это означает, что
lim un = 0. Таким образом, мы получим еще одно доказательство
n→∞
необходимого условия сходимости ряда (см. теорему 1).
П р и м е р. Рассмотрим ряд
1 + 1	+ 1	+ 1	+ ... + 1 + ...,	(30.10)
2	3	4	n

называемый гармоническим, и докажем, что он расходится. При любом натуральном n имеем

+ ... +

2n − 1

n n + 1

2n 2

n слагаемых

Поэтому если 0 < ε < 2 , то для ряда (30.10) нельзя подобрать номера n0, указанного в критерии Коши, так как при любом n = 1, 2, ...

и p = n − 1 не выполняется условие (30.9). Следовательно, гармонический ряд расходится.

Таким образом, условие стремления к нулю последовательности членов ряда, являясь необходимым условием сходимости ряда, не является достаточным для этого.

30.4. Признаки сходимости рядов с неотрицательными членами.

Л е м м а 1. Если члены ряда неотрицательны, то он сходится тогда и только тогда, когда его частичные суммы ограничены

сверху.
Если члены ряда	∞
		(30.11)
	un	(30.11)
	n=1
неотрицательны (un 0, n = 1, 2, ...), то
	sn+1 = sn + un+1 sn,	(30.12)

т. е. последовательность частичных сумм {sn} данного ряда возрастает, а возрастающая последовательность имеет конечный предел тогда и только тогда, когда она ограничена сверху.

§ 30. Числовые ряды

343

З а м е ч а н и е 1. Если члены ряда (30.11) неотрицательны, то последовательность его частичных сумм {sn}, согласно (30.12), возрастает и, следовательно, всегда имеет конечный или бесконечный

предел s, причем	lim sn = sup sn,		(30.13)
s =
и поэтому	n→∞	n
		n = 1, 2, ...	(30.14)
sn s,
∞
Если s = +∞, то пишут	un = +∞.

n=1

З а м е ч а н и е 2. Ряд с неотрицательными членами сходится тогда и только тогда, когда сходится п о к р а й н е й м е р е о д н а п о д- п о с л е д о в а т е л ь н о с т ь последовательности его частичных сумм. Действительно, последовательность частичных сумм ряда с неотрицательными членами возрастает и потому всегда имеет конечный или бесконечный предел, совпадающий, конечно, с пределом любой ее подпоследовательности.

Те о р е м а 5 (интегральный признак Коши сходимости ряда). Если функция f неотрицательна и убывает на полупрямой x 1, то

для того чтобы ряд	∞
		(30.15)
	f (n)	(30.15)
	n=1
сходился, необходимо и достаточно, чтобы сходился интеграл
	+∞
	f (x) dx.	(30.16)

В силу монотонности функции f на промежутке [1, +∞) она ин-

тегрируема по Риману на любом конечном отрезке [1, η], η [1, +∞), и по-

тому имеет смысл говорить о несобственном интеграле (30.16).

Если

k x k + 1, k = 1, 2, ...,

то в силу убывания функции f будем иметь

f (k) f (x) f (k + 1).

Проинтегрировав это неравенство по отрезку [k, k + 1] длины 1 (рис. 122), получим

k+1	k+1	k+1
f (k)	dx f (x) dx f (k + 1)	dx,

344 Гл. 3. Ряды

т. е.	k+1
	k+1
	f (k) f (x) dx f (k + 1).

Просуммировав получившиеся неравенства по k от 1 до n, придем к основному неравенству

n			n		k+1			n
n			n					n
			k			f (x) dx
f (k + 1)						f (x) dx		f (k),
k=1			k=1					k=1
т. е. к неравенству
					n+1
	sn+1 − f (1) f (x) dx sn,								(30.17)
					1
где		n
	sn =			(k),			= 1, 2, ...
	sn =		f	(k),		n	= 1, 2, ...
		k=1
+∞
Если интеграл	f (x) dx сходится, то из неравенства (30.17) в си-
	1
лу неотрицательности подынтегральной функции следует, что
	n+1						+∞
sn+1 f (1) +	f (x) dx f (1) +						f (x) dx < +∞,		(30.18)
	1						1

а поэтому последовательность частичных сумм sn, n = 1, 2, ..., ряда

(30.13) с неотрицательными членами ограничена сверху числом f (1) +

+∞

+f (x) dx. Отсюда согласно лемме 1 следует, что этот ряд сходится.

+∞	f (x) dx расходится, то в силу неотрицатель-
Если же интеграл	f (x) dx расходится, то в силу неотрицатель-
1
ности подынтегральной функции f (x) имеем
n+1		+∞
nlim	f (x) dx =	f (x) dx = +∞,	(30.19)
→∞

атак как согласно неравенству (30.17)

	n+1
sn	f (x) dx,

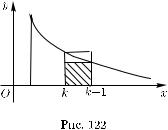
		§ 30. Числовые ряды	345
то, перейдя к пределу в этом неравенстве при			n → ∞, получим
lim	=	Это означает, что ряд (30.13) расходится.
n→∞ sn	(30.19)+∞.	Это означает, что ряд (30.13) расходится.

Для применения интегрального признака к исследованию сходи-

∞

мости ряда un с неотрицательными членами надо подобрать такую

n=1

убывающую функцию f , что f (n) = un, n = 1, 2, ..., и затем исследовать сходимость интеграла (30.16).

Применим этот метод к исследованию сходимости рядов вида

∞	1
		, α R.	(30.20)
n=1	nα	, α R.	(30.20)
n=1

В этом случае при α 0 требуемой функцией, очевидно, является функция f (x) = x1α . Поскольку интеграл

+∞

dx xα

сходится при α > 1 и расходится при α 1, то и ряд (30.20) сходится при α > 1 и расходится при α 1. Расходимость ряда (30.20) при α < 0 ясна непосредственно: последовательность его членов не стремится к нулю, ибо n1α 1 при α < 0.

Те о р е м а 6 (признак сравнения). Пусть

		0 un vn, n = 1, 2, ...					(30.21)
Тогда:	∞				∞
1) если ряд		сходится, то и ряд				сходится;
1) если ряд	vn	сходится, то и ряд			un	сходится;
	n=1				n=1	∞
	∞					∞

2) если ряд	un	расходится, то расходится и ряд					vn.
	n=1					n=1
С л е д с т в и е. Пусть un 0,			vn > 0,		n = 1, 2, ..., и
		lim	un	= l.			(30.22)
		lim		= l.			(30.22)
		n→∞ vn

346 Гл. 3. Ряды

Тогда:

∞

l < +∞, то

если ряд

сходится

сходится и

∞

ряд

n=1

un;

n=1

∞

0 < l +∞,

2) если ряд

расходится и

то расходится

n=1

∞

и ряд

un.

n=1

В частности, если

lim

= 1,

то ряды

un и

vn схо-

n→∞ vn

n=1

дятся и расходятся одновременно.

Д о к а з а т е л ь с т в о

т е о р е м ы. Если ряд

∞

vn сходится, т. е.

∞

def n

n=1

имеет конечную сумму

σ =

vn,

σn =

vk ,

то для любого

n=1

k=1

n = 1, 2, ... выполняется неравенство

σn

σ.

(30.23)

(30.14)

Следовательно,

sn =

vk = σn σ,

(30.24)

k=1

(30.21)k=1

(30.23)

∞

а это в силу леммы означает, что ряд

un сходится.

n=1

Если ряд

un расходится, то расходится и ряд

vn, так как

n=1

если бы он сходился, то в силу уже доказанного сходился бы и ряд

∞

un.

n=1						∞
						∞
Д о к а з а т е л ь с т в о с л е д с т в и я. Пусть ряд						vn сходится.
						n=1
	l < +
Поскольку	l < +	∞	, то в силу условия (30.22) существует такой номер
Поскольку		∞			un	< l + 1, а следо-
n0, что для всех n > n0 выполняется неравенство
n0, что для всех n > n0 выполняется неравенство					vn
вательно, и неравенство
			un < (l + 1)vn, n > n0.			(30.25)
	∞				∞	(l + 1)vn (теоре-
Если ряд		vn сходится, то сходится и ряд		n=1		(l + 1)vn (теоре-
	n=1			n=1

ма 2), а поэтому по признаку сравнения (теорема 6) в силу неравен-

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 4535 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.08.2019218.11 Кб3контрольная работа №3 по ВМ(2011).doc
#
24.09.2019317.95 Кб16Копия Т Ф К П.doc
#
10.05.20151.13 Mб10КР по ТПР Чекменёв А.С..docx
#
10.05.2015649.22 Кб79КР_Ромашин_РС110_2012_1.doc
#
24.09.2019131.07 Кб6КРАТКАЯ ХАРАКТЕРИСТИКА ОСНОВНЫХ АХОВ.doc
#
10.05.20155.57 Mб776Краткий курс математического анализа. Том 1.pdf
#
10.05.20154.49 Mб350Краткий курс математического анализа. Том 2.pdf
#
10.05.20151.56 Mб91краткое сожержание курса БЖД.doc
#
16.11.201929.92 Кб34кризис.docx
#
16.03.20162.51 Mб732Криминология Малков В. Д..doc
#
27.11.2019524.29 Кб71Курс лекций Интернет-технологии.doc