
Краткий курс математического анализа. Том 1
.pdf

308 Гл. 2. Интегральное исчисление функций одной переменной
Обозначим через qτ и Qτ тела, образованные вращением вокруг оси x ступенчатых фигур pτ и Pτ (см. (28.6)), соответствующих некоторому разбиению τ отрезка [a, b]. Из включения pτ p Pτ следует включение qτ Q Qτ , a следователь-
но, и неравенство |
|
μqτ V = μQ μQτ . |
(28.35) |
Объемы μqτ и μQτ равны суммам объемов составляющих их цилиндров, обра-
зованных |
вращением прямоугольников |
|||||||||
pτ ,k и Pτ ,k (см. (28.4) и (28.5)): |
|
|
|
|
||||||
|
|
kτ |
|
|
|
kτ |
|
|
|
|
|
|
|
πm2 |
|
|
|
|
2 |
|
|
μq |
τ |
= |
x |
, |
μQ = |
πM |
x |
k |
||
|
|
k |
k |
|
τ |
|
k |
|
||
|
|
k=1 |
|
|
|
k=1 |
|
|
|
|
(рис. 116). Из этих равенств видно, что μqτ и μQτ являются соответственно нижними и верхними суммами Дарбу функции πf 2(x), поэтому
|
b |
|
lim μqτ = |
lim μQτ = π |
f 2(x) dx, |
|τ |→0 |
|τ |→0 |
|
|
a |
|
откуда в силу (28.35) и следует, что |
|
|
|
b |
|
V = π f 2(x) dx. |
(28.36) |
|
a
П р и м е р. Найдем объем тела, получающегося от вращения вокруг оси x одной арки синусоиды y = sin x:
π |
|
π |
|
π |
π2 |
|
2 |
π |
|
π |
|
||
V = π sin x dx = |
|
dx − |
|
cos 2x dx = |
|
. |
2 |
2 |
2 |
||||
0 |
|
0 |
|
0 |
|
|
28.6.Теоремы Гульдина. Центры тяжести плоских фигур
иих моменты относительно осей. Пусть Γ — график неотрица-
тельной непрерывно дифференцируемой на отрезке [a, b] функции f , τ = {xk }kk==k0τ — разбиение этого отрезка, а λτ — ломаная, соответствующая этому разбиению и вписанная в кривую Γ. Будем кривую Γ и ломаные λτ рассматривать как материальные кривые, т. е. как имеющие массу. Будем предполагать, что их линейные плотности равны единице. Это означает, что массы их частей совпадают с длинами этих частей.

§ 28. Приложения определенного интеграла |
309 |
|||||
Как и выше (см. п. 28.4), положим |
|
|
|
|||
yk = f (xk ), |
xk = xk − xk−1, |
yk = yk − yk−1, |
|
|||
Δ(λτ )k ≡ |
|
= 1 + f 2(ξk) xk , |
|
|||
xk2 + yk2 |
|
|||||
ξk [xk−1, xk], k = 1, 2, ..., kτ . |
|
|||||
Рассмотрим физический смысл суммы |
|
|
|
|||
kτ |
kτ |
|
|
|
|
|
|
|
|
|
|
|
|
k=1 f (ξk)Δ(λτ )k |
= k=1 f (ξk) 1 + f 2 |
(ξk) xk , |
(28.37) |
|||
являющейся, очевидно, интегральной суммой функции y 1 + y 2 , y = = f (x), и потому имеющей своим пределом при |τ | → 0 интеграл
b |
|
b |
|
a y |
|
dx = a y ds. |
(28.38) |
1 + y 2 |
Каждое слагаемое f (ξk)Δ(λτ )k суммы (28.37) является произведением массы Δ(λτ )k k-го звена ломаной λτ на некоторое среднее расстояние f (ξk) этого звена от оси x, т. е. f (ξk)Δ(λτ )k является приближенным значением момента k-го звена ломаной λτ относительно оси x, а вся сумма (28.37) представляет собой приближенное значение момента этой ломаной относительно той же оси. Предел этих приближенных значений моментов ломаных λτ при |τ | → 0 равен моменту Mx кривой Γ относительно оси x. Поскольку сумма (28.37) при |τ | → 0 стремится к интегралу (28.38), то
b |
|
Mx = y ds. |
(28.39) |
a |
|
Этот момент равен моменту относительно оси x материальной точки, масса которой равна массе кривой Γ (в данном случае совпадающей с ее длиной S), помещенной в центр тяжести (x0, y0) этой кривой. Момент относительно оси x материальной точки массы S, находящейся в точке (x0, y0), равен Sy0. В силу сказанного он совпадает с моментом
Mx, т. е. |
= Mx. |
(28.40) |
Sy0 |
Используя формулу (28.39), это равенство можно записать в виде
b |
b |
Sy0 = |
y ds. Умножив обе его части на 2π и вспомнив, что 2π y ds |
a |
a |
является площадью L поверхности вращения (см. п. 28.4), получим, что

§ 28. Приложения определенного интеграла |
311 |
Если кривая Γ не удовлетворяет условиям, при которых получена формула (28.39), то можно попытаться разбить кривую Γ на конечное число кривых, каждая из которых уже удовлетворяет указанным условиям, и воспользоваться тем, что момент относительно оси объединения тел равен сумме их моментов.
Перейдем ко второй теореме Гульдина.
Пусть функции f и g непрерывны на отрезке [a, b], 0 g(x) f (x),
x [a, b], |
def |
|
|
|
|
|
(28.44) |
||||
|
P = {(x, y) : a x b, g(x) y f (x)}; |
||||||||||
как всегда, τ = {xk }kk==0kτ |
— разбиение отрезка [a, b], |
|
|
|
|
||||||
|
|
xk = xk − xk−1, |
ξk [xk−1, xk ], |
|
|
|
|
||||
а Pτ — на этот раз ступенчатая фигура, состоящая из прямоуголь- |
|||||||||||
ников |
Pτ ,k = {(x, y) : xk−1 x xk , g(ξk) y f |
(ξk)} |
|||||||||
|
|
||||||||||
с основаниями и высотами, равными соответственно |
xk и f (ξk) − |
||||||||||
− g(ξk), k = 1, 2, ..., kτ (рис.118): |
|
|
|
|
|
|
|
|
|||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
Pτ = kτ |
Pτ ,k. |
|
|
|
|
|||
|
|
|
=1 |
|
|
|
|
|
|
|
|
Будем рассматривать фигуры P и Pτ как материальные, т. е. как |
|||||||||||
фигуры, имеющие массу с плотно- |
|
|
|
|
|||||||
стью 1. Это означает, что масса каждой |
|
|
|
|
|||||||
|
|
|
|
||||||||
из их частей совпадает с площадью этой |
|
|
|
|
|||||||
части. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Центр тяжести прямоугольника Pτ ,k |
|
|
|
|
|
||||||
находится в его центре и, следовательно, |
|
|
|
|
|
|
|||||
на расстоянии |
|
|
|
|
|
|
|
|
|
||
|
1 |
[f (ξk) + g(ξk)] |
(28.45) |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
от оси x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Момент прямоугольника Pτ ,k относительно оси x равен произведению ор-
динаты его центра тяжести (28.45) на
его массу, т. е. в данном случае на площадь [f (ξk) − g(ξk)]Δxk. Таким образом, этот момент равен
12 [f 2(ξk) − g2(ξk)]Δxk .
Для момента же Mτ ступенчатой фигуры Pτ , равного сумме моментов составляющих его прямоугольников Pτ ,k, имеем формулу
kτ
Mτ = 12 [f 2(ξk) − g2(ξk)]Δxk . (28.46)
k=1

312 Гл. 2. Интегральное исчисление функций одной переменной
Момент Mx самой фигуры P относительно оси x равен пределу моментов Mτ ступенчатых фигур при |τ | → 0:
Mx = lim Mτ . |
(28.47) |
|τ |→0 |
|
Сумма, стоящая в правой части равенства (28.46), представляет
собой интегральную сумму функции |
1 |
[f 2(x) − g2(x)], поэтому имеем |
|||||||||
2 |
|||||||||||
также |
|
|
|
|
b |
|
|
|
|
||
lim |
M |
τ |
= |
1 |
[f 2(x) |
− |
g2 |
(x)] dx. |
(28.48) |
||
|
|||||||||||
τ 0 |
|
2 |
|
|
|
|
|
|
|||
| |→ |
|
|
|
|
|
|
|
|
|
|
|
a
Таким образом, из (28.47) и (28.48) следует, что момент Mx фигуры P относительно оси x равен интегралу, стоящему в правой части формулы (28.48):
b |
|
Mx = 21 [f 2(x) − g2(x)] dx. |
(28.49) |
a
Момент фигуры относительно оси равен моменту материальной точки, масса которой равна массе фигуры и которая помещена в центр тяжести фигуры.
Поэтому если (x0, y0) — центр тяжести фигуры P , то, так как ее масса в данном случае совпадает с ее площадью S, получим
|
|
Mx = Sy0, |
(28.50) |
|
или, в силу (28.49), |
b |
|
||
|
1 |
|
||
Sy0 = |
[f 2(x) − g2(x)] dx. |
|||
2 |
||||
|
|
a |
|
|
Умножим обе части последнего равенства на 2π: |
||||
|
|
b |
b |
|
S · 2πy0 = π |
f 2(x) dx − π |
g2(x) dx. |
||
|
|
a |
a |
|
В правой части этого равенства стоит разность объемов тел, полученных вращением вокруг оси x криволинейных трапеций, порожденных графиками соответственно функций f и g (п. 28.5), т. е. объем V тела, получающегося вращением фигуры P вокруг оси x:
V = S · 2πy0. |
(28.51) |
Таким образом, доказана следующая Те о р е м а 2 (вторая теорема Гульдина). Объем тела, получен-
ного вращением плоской фигуры вокруг оси, равен площади фигуры, умноженной на длину окружности, описываемой центром тяжести фигуры.
§ 29. Несобственные интегралы |
313 |
Здесь под плоской фигурой понимается множество P рассмотренного выше типа (см. (28.44)), а под ее вращением — вращение этой фигуры вокруг оси, лежащей с фигурой в одной плоскости и не пересекающей ее.
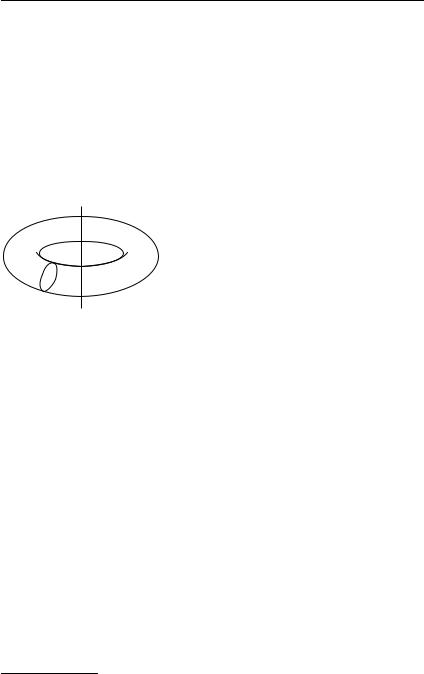
П р и м е р. Найдем объем V тора, рассмотренного в качестве примера применения первой теоремы Гульдина. Поскольку площадь вращаемой фигуры (в данном случае круга) равна πr2, то в силу
формулы (28.51)
V = πr2 · 2πa = 2π2r2a.
Отметим в заключение, что для координаты x0 центра тяжести фигуры P имеет место формула (аналогичная формуле (28.50))
My = Sx0, |
(28.52) |
где момент My фигуры P находится по формуле, аналогичной формуле (28.49).
Из формул (28.50) и (28.52) получаются следующие формулы для координат центра тяжести (x0, y0) фигуры P :
x0 = My /S, y0 = Mx/S.
§29. Несобственные интегралы
29.1.Определение несобственных интегралов. Пусть
функция f определена на конечном или бесконечном полуинтервале [a, b), −∞ < a < b +∞, и для любого числа η [a, b) интегрируема
на отрезке [a, η].
η
О п р е д е л е н и е 1. Функция F (η) = f (x) dx верхнего предела
a
интегрирования, a η < b, называется несобственным интегралом
и обозначается
b
f (x) dx.
a |
|
|
η |
Если существует конечный предел lim |
f (x) dx, то несобственный |
η→b |
b |
b |
интеграл f (x) dx называется сходящимся, а если этот предел не
a
существует, то — расходящимся.
В случае когда несобственный интеграл сходится, говорят также, что он существует, а если расходится, то не существует.

314 Гл. 2. Интегральное исчисление функций одной переменной
b |
η |
|
Если интеграл f (x) dx сходится, то предел lim |
f (x) dx обозна- |
||
a |
η→b |
b |
|
чается тем же символом, что и сам интеграл, т. е. |
|||
|
|||
b |
η |
|
|
def |
lim f (x) dx, |
(29.1) |
|
f (x) dx = |
|||
|
η→b |
|
|
a |
a |
|
|
и для краткости также называется несобственным интегралом (иногда — его значением).
Подчеркнем, что здесь возможны два случая: когда b — конечное число и когда b равно бесконечности (рис. 119).
Если b конечно, а функция f интегрируема на |
отрезке [a, b], |
|
то в |
силу непрерывности интеграла (свойство 9 в |
п. 24.1) предел |
η |
b |
|
|
||
lim |
f (x) dx, a η < b, существует и равен интегралу |
f (x) dx. Таким |
η→b |
a |
|
a |
||
образом, интеграл Римана является частным случаем несобственного интеграла.
При условии конечности b определение 1 содержательно, только если функция f неограничена в любой окрестности точки b (см. рис. 119): если функция f ограничена на полуинтервале [a, b) и для любого η [a, b] она интегрируема по Риману на отрезке [a, η], то
b
нетрудно убедиться, что несобственный интеграл f (x) dx существует
a
и совпадает с интегралом Римана функции f , произвольно доопределенной в точке x = b (почему?).
Таким образом понятие несобственного интеграла содержательно (в том смысле, что оно является новым понятием) лишь в том случае, когда график неинтегрируемой функции неограничен. В случае неограниченного промежутка, по которому ведется интегрирование, это обусловливается во всяком случае уже неограниченностью
§ 29. Несобственные интегралы |
315 |
указанного промежутка, а в случае конечности этого промежутка неограниченностью подынтегральной функции.
Для отличия интеграла Римана от несобственного интеграла интеграл Римана называют иногда собственным интегралом.
b
Геометрический смысл несобственного интеграла f (x) dx от неот-
a
рицательной функции f состоит в том, что он, подобно собственному интегралу, равен площади криволинейной трапеции
P = {(x, y) : a x < b, 0 y f (x)},
порожденной графиком функции f , причем эта трапеция (как в случае неограниченной функции f и конечного промежутка [a, b), так и в случае бесконечного промежутка [a, b)) всегда является (в отличие от того, что имело место для собственного интеграла) н е о г р а н и ч е н- н ы м м н о ж е с т в о м.
Если a < c < b, то из равенства
η |
c |
η |
|
|
f (x) dx = f (x) dx + f (x) dx |
(29.2) |
|
a |
a |
c |
|
сразу видно, что несобственный интеграл (29.1) существует в том
и |
только том |
случае, когда |
существует несобственный интеграл |
||||
b |
|
|
η |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) dx = lim |
f (x) dx, причем в случае существования этих инте- |
|||||
c |
|
η→b c |
|
|
|
|
|
гралов, перейдя в равенстве (29.1) к пределу при η → b, получим |
|||||||
|
|
|
b |
|
c |
b |
|
|
|
|
|
f (x) dx = |
f (x) dx + |
f (x) dx. |
(29.3) |
|
|
|
a |
|
a |
c |
|
|
|
|
b |
b |
|
|
c |
В этом равенстве и |
— несобственные интегралы, а |
— собственный |
|||||
интеграл. |
|
a |
c |
|
|
a |
|
|
|
|
|
|
|
||
Если функция f определена на полуинтервале (a, b], −∞ a <
< b < +∞, и при любом ξ (a, b] интегрируема по Риману на отрезке
b
[ξ, b], то аналогично формуле (29.1) несобственный интеграл f (x) dx
b |
a |
|
определяется как функция F (ξ) = f (x) dx нижнего предела интегри-
ξ
рования, a < ξ b.


 ма, лежит в одной плоскости с указанной
ма, лежит в одной плоскости с указанной

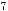 которой находится на расстоянии
которой находится на расстоянии