Задача коммивояжера

Агент по сбыту собирается посетить каждый из n городов по одному разу, выехав из одного города и вернувшись в него же. Обозначим расстояние между городами i и j как c_ij. Тогда задача коммивояжера математически буде записана следующим образом:

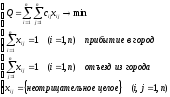
Решить задачу коммивояжера – это значит найти цикл. Данная задача является частным случаем целочисленного программирования. Одним из методов решения такой задачи будет метод ветвей и границ, суть которого состоит из двух этапов: вычисление нижней границы и ветвление. Метод ветвей и границ довольно трудоемок, поэтому мы будем решать задачу коммивояжера табличным способом.

Условия задачи коммивояжера задаются в виде матрицы расстояний, причем, если дуги x_ix_j нет в графе задачи, то вместо c_ij будет “-“, при чем не обязательно c_ij=c_ji.

j i	1	2	…	n
1	-	c12	…	c1n
2	c21	-	…	c2n
…	…	…	…	…
n	cn1	cn1		-

Решим задачу коммивояжера на примере конкретной задачи, заданной следующей матрицей расстояний:

	A1	A2	A3	A4	A5	A6	min
A1		68	73	24	70	9	9
A2	58		16	44	11	92	11
A3	63	9		86	13	18	9
A4	17	34	76		52	70	17
A5	60	18	3	45		58	3
A6	16	82	11	60	48		11

Первым действием в решении данной задачи является так называемая операция приведения матрицы, которая основывается на том, что при уменьшении чисел какой-либо строки на одно и то же число длины всех маршрутов уменьшаются на это же число, так как в длину каждого маршрута в качестве слагаемого входят только по одному числу из каждой строки (столбца). Кратчайший маршрут при этом сохраняется, но его длина уменьшается на это число.

В последнем столбце таблицы записаны минимальные значения по строкам. Вычитая эти числа из соответствующих строк, получим следующую таблицу:

	A1	A2	A3	A4	A5	A6
A1		59	64	15	61	0
A2	47		5	33	0	81
A3	54	0		77	4	9
A4	0	17	59		35	53
A5	57	15	0	42		55
A6	5	71	0	49	37	
min	0	0	0	15	0	0

Вычитая число 15 из столбца А4, мы получаем новую таблицу, которая называется приведенной:

	A1	A2	A3	A4	A5	A6	min
A1		59	64	0	61	0	0
A2	47		5	18	0	81	01
A3	54	0		62	4	9	0
A4	0	17	59		35	53	0
A5	57	15	0	27		55	0
A6	5	71	0	34	37		0
min	0	0	0	0	0	0

Числа, которые вычитались, называются постоянными приведения. Так как каждая постоянная приведения входит как слагаемое в длину любого маршрута, то за нижнюю границу можно принять сумму всех постоянных приведения: L=L₀+l, где l=(9+11+9+17+3+11)+(15)=75. Это начальный шаг алгоритма (применяется однократно).

Следующим шагом алгоритма является ветвление, так называемый общий шаг, который применяется неоднократно. Каждый раз нужно определить способ ветвления, а именно, выбирается дуга x_ix_j и всё множество маршрутов  разбивается на два подмножества: подмножество маршрутов ₂, содержащих дугу x_ix_j и подмножество ₁, не содержащих дугу x_ix_j.

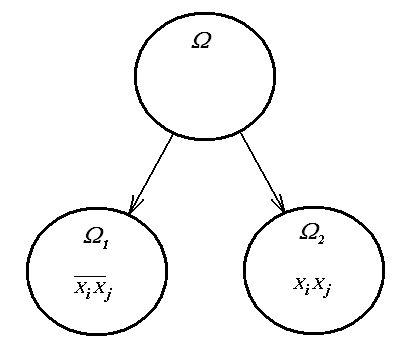
Множество ₁ получается из множества  исключением маршрутов, содержащих дугу x_ix_j. Исключать дугу мы будем в матрице расстояний замещением расстояния c_ij символом “”. Дуга для ветвления выбирается так, чтобы нижняя граница множества ₁(x_ix_j) была, по возможности, большой, т.е. чтобы при исключении этой дуги была большей сумма возникающих при этом постоянных приведения. Положительные постоянные приведения возникают лишь в том случае, когда в одном из соответствующих рядов x_ix_j матрицы расстояний нет нулевых элементов.

Дугами ветвления могут быть дуги, для которых расстояние равно нулю. В нашем случае дугами ветвления могут быть x₁x₄ (9+18=18),x₁x₆ (0+9=9),x₂x₅ (5+4=9),x₃x₂ (4+15=19),x₄x₁ (17+5=22),x₅x₃ (15+0=15),x₆x₃ (5+0-5). В скобках указаны суммы постоянных приведения соответствующих нулевых расстояний. Очевидно, что дугой с максимальной суммой является x₄x₁, которую мы и выбираем для ветвления.

Матрица для подмножества 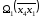дана следующей таблицей, для которой суммы постоянных приведения равна 5+17=22.

	A1	A2	A3	A4	A5	A6	min
A1		59	64	0	61	0	0
A2	47		5	18	0	81	0
A3	54	0		62	4	9	0
A4	“”	17	59		35	53	17
A5	57	15	0	27		55	0
A6	5	71	0	34	37		0
min	5	0	0	0	0	0

Конечно «перебор» не является оптимальной процедурой. Более приемлемым является соображение наличия «нулевой» дуги (в нашем случае x₁x₄ и x₄x₁).

Матрица ₂(x₄x₁) получается в результате следующих действий:

1. исключаем строку А₄ и столбец А₁;

2. исключаем противоположную дугу x₁x₄ заменой расстояния с₁₄на «»;

3. следим за тем, чтобы из ранее включенных в маршрут дуг и этой дуги не могли образовываться замкнутые контуры, не содержащие всех пунктов.

После исключения строки А₄ и столбца А₁ получаем следующую матрицу:

	A2	A3	A4	A5	A6	min
A1	59	64	“”	61	0	0
A2		5	18	0	81	0
A3	0		62	4	9	0
A5	15	0	27		55	0
A6	71	0	34	37		0
min	0	0	18	0	0

Сумма постоянных приведения равна 18. На следующей схеме представлен результат ветвления.

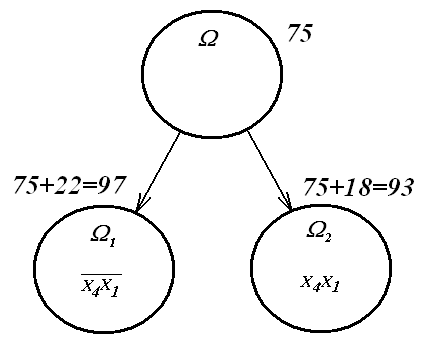
Большее значение нижней границы для ₁ (97) по сравнению с нижней границей для ₂ (93) позволяет надеяться, что в дальнейшем это множество будет отсечено. В качестве «более перспективного» выберем множество ₂ и будем подвергать его ветвлению.

После вычитания суммы 18 из чисел столбца А₄ получим матрицу:

	A2	A3	A4	A5	A6
A1	59	64	“”	61	0
A2		5	0	0	81
A3	0		44	4	9
A5	15	0	9		55
A6	71	0	16	37	

Нулевые дуги и сумма соответствующих постоянных приведения для данной матрицы будут следующими: x₁x₆ (59+9=68),x₂x₄ (0+9=9),x₂x₅ (0+4=4),x₃x₂ (4+15=19),x₅x₃ (0+9=9),x₆x₃ (16+0=16). Максимальной из всех сумм постоянных приведения равна 68, что соответствует дуге x₁x₆. Таким образом, множество ₂ нужно разбить на два непересекающихся подмножества и₄(x₁x₆). Нижняя граница ₃ равна сумме нижней границы ₂ и 68, т.е. 93+68=161.

Для получения нижней границы ₄ нужно выполнить следующие действия:

1. вычеркнем строку А₁ и столбец А₆;

2. заменим элемент с₆₄ на “”, так как если этого не сделать, то будет замкнутый контур x₄→x₁→x₆→x₄ в который не все вершины входят.

В результате чего получим следующую матрицу расстояний для подмножества ₄:

	A2	A3	A4	A5	min
A2		5	0	0	0
A3	0		44	4	0
A5	15	0	9		0
A6	71	0	“”	37	0
min	0	0	0	0

Как видно из матрицы, отличных от нуля постоянных приведения нет, поэтому нижняя граница ₄ совпадает с нижней границей ₂ и равна 93+0=93.

Выбираем среди «нулевых» дуг дугу с максимальной суммой постоянных приведения: x₂x₄ (0+9=9),x₂x₅ (0+4=4),x₃x₂ (4+15=19),x₅x₃ (0+9=9)x₆x₃ (37+0=37). Это дуга x₆x₃. Нижняя граница для подмножества ₅ равна 93+37=130 и ее дальнейшее ветвление под большим вопросом.

Матрица ₆ получается вычеркиванием строки А₆ и столбца А₃. Так как путь x₄→x₁→x₆→x₃ не должен превращаться в контур, то элемент с₃₄ нужно заменить на «». В результате матрица ₆ имеет вид:

	A2	A4	A5	min
A2		0	0	0
A3	0	“”	4	0
A5	15	9		9
min	0	0	0

Сумма постоянных приведения на данном этапе равна 9+0=9. Нижняя граница множества ₆ будет равна 93+9=102. После вычитания числа 9 из строки А₅ получим матрицу:

	A2	A4	A5
A2		0	0
A3	0	“”	4
A5	6	0	

Рассматривая полученную матрицу ₆ как множество для ветвления, выберем среди «нулевых» дуг дугу с максимальной суммой постоянных приведения: x₂x₄ (0+0=0),x₂x₅ (0+4=4),x₃x₂ (4+6=10),x₅x₄ (6+0=6). Это дуга x₃x₂. Множество ₆ делится на два подмножества 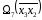и₈(x₃x₂). Нижняя граница для ₇ будет равна нижней границе для ₆ плюс сумма постоянных приведения (10): 102+10=112.

Чтобы получить матрицу ₈ нужно вычеркнуть строку А₃ и столбец А₂ и вместо элемента с₂₄ поставить прочерк “”:

	A4	A5
A2	“”	0
A5	0	

Матрица ₈ является приведенной, и поэтому нижние границы ₈ и ₆ совпадают и равны 102. Остается включить в маршрут единственно возможные дуги x₂x₅ и x₅x₄. Получаем замкнутый маршрут x₄→x₁→x₆→x₃→x₂→x₅→x₄ с длиной пути l=102.

Остается сделать последний шаг: проверка оптимальности решения. Для этого нужно сравнить длину полученного замкнутого маршрута (102) с нижними границами концевых множеств схемы ветвления: 112, 130, 161 и 97. В нашем случае существует множество ₁ с меньшим значением длины 97<102. Применим схему ветвления к множеству ₁.

Так как матрица ₁ не является приведенной, то вычтем из строки А₄ число 17, а из столбца А₁ число 5 и получим приведенную матрицу :

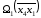	A1	A2	A3	A4	A5	A6	min
A1		59	64	0	61	0	0
A2	42		5	18	0	81	0
A3	49	0		62	4	9	0
A4	“”	0	42		18	36	0
A5	52	15	0	27		55	0
A6	0	71	0	34	37		0
min	0	0	0	0	0	0

Нулевые дуги и сумма соответствующих постоянных приведения для данной матрицы будут следующими: x₁x₄ (0+18=18),x₁x₆ (0+19=19),x₂x₅ (5+4=9),x₃x₂ (4+0=4),x₄x₂ (18+0=18),x₅x₃ (15+0=15), x₆x₁ (0+42=42),x₆x₃ (0+0=0). Максимальная сумма из всех сумм постоянных приведения равна 42, что соответствует дуге x₆x₁. Таким образом, множество 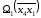делится на два подмножества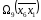и₁₀(x₆x₁).

Нижняя граница подмножества 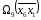равна нижней границе множестваплюс 42 (139), что больше 102, и, следовательно, множество₉ не является оптимальным.

Чтобы получить матрицу расстояний ₁₀, нужно из матрицы ₁ вычеркнуть строку А₆ и столбец А₁ и элемент с₁₆ заменить прочерком “”.

	A2	A3	A4	A5	A6	min
A1	59	64	0	61	“”	0
A2		5	18	0	81	0
A3	0		62	4	9	0
A4	0	42		18	36	0
A5	15	0	27		55	0
min	0	0	0	0	9

После приведения данной матрицы нижняя граница для ₁₀ будет равна 97+9=106, что больше, чем 102.

Следовательно, найденный маршрут x₄→x₁→x₆→x₃→x₂→x₅→x₄ является кратчайшим с длиной пути l=102.

Окончательно вся схема ветвления представлена ниже.

Задание 5.

Найти кратчайший из замкнутых маршрутов, проходящих точно по одному разу через каждый из шести городов А₁, А₂, А₃, А₄, А₅ и А₆. Расстояния между городами заданы следующей таблицей:

	А1	А2	А3	А4	А5	А6
А1	-	30	25	17	39	18
А2	31-2k	-	26	25	30	42-n
А3	28	27	-	29	18+n	40
А4	37	16+m	21	-	17	25
А5	19	23	25	31	-	19
А6	21	27	32	16	19+k	-

44