
- •Санкт-петербургский университет
- •Введение
- •Литература
- •Графический способ решения задачи линейного программирования
- •Симплекс–метод
- •Алгоритм симплекс-метода
- •Транспортная задача. Общие понятия
- •Математическая постановка транспортной задачи
- •Методы нахождения опорного плана
- •1. Метод северо-западного угла
- •2. Метод минимального элемента
- •3. Метод аппроксимации Фогеля
- •Метод потенциалов нахождения оптимального плана транспортной задачи
- •Выбор кратчайшего пути
- •Задача коммивояжера
Симплекс–метод
Задача линейного программирования записывается в основной форме: максимум целевой функции Q при выполнении условий, заданных в форме равенств.
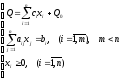
Пусть x1, x2, … , xm – m базисных переменных; хm+1, xm+2, …, xn – (n-m) свободных переменных. Базисные переменные выражают через свободные в результате операции исключения, целевую функцию также выражают через свободные переменные.
Тогда ЗЛП будет
записана в канонической
форме (отличными
от нуля будут коэффициенты целевой
функции только для свободных переменных):Q=
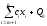 →max
→max


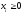 (i=
(i=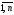 )
)
Векторная форма ЗЛП представляет простой способ ее записи и решения. Введем следующие обозначения:
X= -
вектор-столбец переменных;
-
вектор-столбец переменных;
θ= -
нудь-вектор размерностиm;
-
нудь-вектор размерностиm;
С=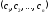 - вектор-строка коэффициентов целевой
функции;
- вектор-строка коэффициентов целевой
функции;
В= - вектор-столбец свободных членов;
- вектор-столбец свободных членов;
Р= - симплекс-матрица.
- симплекс-матрица.

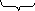
m
n-m
Таким образом, в
векторной форме задача линейного
программирования записывается в виде:
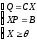 .
.
Для каждой из
свободных переменных определяют
вспомогательное число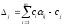 (
(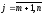 ),
которое для всех базисных переменных
равно нулю
),
которое для всех базисных переменных
равно нулю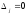 (
( ).
).
Теорема о признаках оптимальности опорного плана:
Опорный план
 является оптимальным, если
является оптимальным, если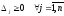 .
.Если для некоторого значенияj (допустим числа k)
 и все
и все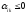
 ,
то ЗЛП неразрешима.
,
то ЗЛП неразрешима.Если для опорного плана X
 ,
то существует другой знак X`,
такой, что Q(x’)>Q(x).
,
то существует другой знак X`,
такой, что Q(x’)>Q(x).
Для перехода к
новой симплекс-таблице необходимо
вычислить
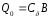 - скалярное произведениевектор-строки
базисных элементов целевой функции и
вектор-столбца свободных членов,
вспомогательные величины
- скалярное произведениевектор-строки
базисных элементов целевой функции и
вектор-столбца свободных членов,
вспомогательные величины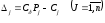 ,
где
,
где -j-ый
столбец симплекс-таблицы,
-j-ый
столбец симплекс-таблицы,
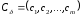 - базис.
- базис.
Если существуют
отрицательные значения ,
то в базис вводят новый вектор
,
то в базис вводят новый вектор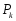 .Находятmin
.Находятmin для всех положительных
для всех положительных
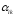 .
Пусть это будетi=r.
Тогда из базиса исключают вектор
.
Пусть это будетi=r.
Тогда из базиса исключают вектор
 .Элемент
.Элемент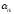 называется разрешающим элементом.
называется разрешающим элементом.
Новый опорный план находят по формулам Жордана-Гаусса:
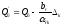 ;
;

если i≠r
если i=r
 ;
;

если i≠r
если i=r
Алгоритм симплекс-метода
Находят опорный план
Составляют симплекс-таблицу
Выясняют разрешимость ЗЛП
Если существуют
 ,
тогда определяют номер разрешающего
столбца по максимуму |
,
тогда определяют номер разрешающего
столбца по максимуму | |
|Для данного к определяют номер разрешающей строки по минимуму.
 для
всех положительных элементов разрешающего
столбца симплекс-матрицы.
для
всех положительных элементов разрешающего
столбца симплекс-матрицы.По формулам определяют
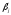 ,
, и
и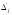 .
.Составляют новую симплекс-таблицу.
См. пункт 3.
Задача. Определить план изготовления изделий А, В и С, обеспечивающий максимальный их выпуск в стоимостном выражении с учётом ограничений на возможное использование сырья трёх видов.
|
Вид сырья |
Нормы расхода сырья на кг изделия |
Общее количество сырья | |||
|
А |
В |
С |
| ||
|
I |
18 |
15 |
12 |
360 | |
|
II |
6 |
4 |
8 |
192 | |
|
III |
5 |
3 |
3 |
180 | |
|
Цена одного изделия |
9 |
10 |
16 |
| |
Составим математическую модель данного производства. Введем следующие обозначения: x1 – выпуск изделий А; x2 – выпуск изделий В; х3 – выпуск изделий С.
Запишем выражение для целевой функции (общая стоимость проданных изделий, которая должна быть максимальной):
Q=9x1+10x2+16x3→max.
Исходя из запасов сырья и неотрицательности количества выпускаемых изделий, составляем условия ограничения:
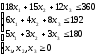
Для решения задачи симплекс-методом переведем ЗЛП в основную форму, превратив неравенства в равенства, для чего введем новые неотрицательные переменные х4, х5, х6:
18х1 + 15х2 +12х3 + х4 = 360
6х1 + 4х2 + 8х3 +х5 = 192
5х1 + 3х2 +3х3 + х6 = 180
Введенные новые переменные имеют следующий экономический смысл: х 4 – неизрасходованное количество сырья А; х5 - неизрасходованное количество сырья В; х6 - неизрасходованное количество сырья С.
Векторы для новых
переменных Р4
=
 ,
Р5
=
,
Р5
=
 ,
Р6
=
,
Р6
=
 являются единичными,
т.е. введенные переменные {х4,
х5,
х6}
представляют базис, а остальные переменные
{х1,х2,
х3}
являются свободными, следовательно,
опорный план имеет вид: Х=(
являются единичными,
т.е. введенные переменные {х4,
х5,
х6}
представляют базис, а остальные переменные
{х1,х2,
х3}
являются свободными, следовательно,
опорный план имеет вид: Х=(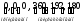 ).
).
Значение целевой функции равно Qo=9·0+10·0+16·0=0 (усл. ед.): ничего не произвели – ничего не получили.
Таблица. Исходная симплекс-таблица данной задачи
|
i |
Базис |
Сб |
βi |
9 |
10 |
16 |
0 |
0 |
0 |
|
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 | ||||
|
1 |
Р4 |
0 |
360 |
18 |
15 |
12 |
1 |
0 |
0 |
|
2 |
Р5 |
0 |
192 |
6 |
4 |
8 |
0 |
1 |
0 |
|
3 |
Р6 |
0 |
180 |
5 |
3 |
3 |
0 |
0 |
1 |
|
4 |
|
|
0 |
-9 |
-10 |
-16 |
0 |
0 |
0 |
Рассчитаем исходные значения целевой функции Qo=СбВ=360·0+192·0 + 180·0=0 и вспомогательных величин Δj=CбPj–Cj:
Δ1 = P1Cб–C1=18·0+6·0+5·0–9=-9,
Δ2 = P2Cб–C2=15·0+4·0+3·0–10=-10
Δ3 = P3Cб–C3=12·0+8·0+3·0–16=-16
Отрицательные числа Δj свидетельствуют о возможности увеличения общей стоимости продукции и показывают насколько увеличится сумма при введении в план единицы продукции.
Максимальное
значение модуля вспомогательной величины
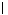 Δj
Δj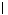 равно 16, следовательно, номер разрешающего
столбца к=3.
равно 16, следовательно, номер разрешающего
столбца к=3.
Для данного столбца
все
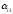 >
0. Находим минимальное значение
>
0. Находим минимальное значение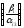 :min
:min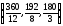 =
min{30,
24, 60} = 24. Следовательно, номер разрешающей
строки r
= 2. Таким образом, разрешающий элемент
=
min{30,
24, 60} = 24. Следовательно, номер разрешающей
строки r
= 2. Таким образом, разрешающий элемент
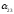 = 8. Вводим в базис вектор Р3,
выводим из базиса вектор Р5.
Все элементы данной новой строки
вычисляются делением на разрешающий
элемент
= 8. Вводим в базис вектор Р3,
выводим из базиса вектор Р5.
Все элементы данной новой строки
вычисляются делением на разрешающий
элемент
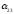


Остальные элементы вычисляются по правилу треугольника, согласно которому находятся три числа:
число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы (число А);
число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы и столбца, соответствующего вектору, вводимому в базис (число С);
число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора (число В).
Искомый элемент новой симплекс-таблицы вычисляется по формулам Жордана-Гаусса: А-В∙С.
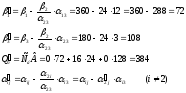
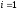


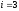


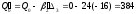
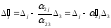

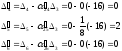
Таким образом, новая симплекс-таблица представлена в следующей таблице.
|
i |
Базис |
Сб |
βi |
9 |
10 |
16 |
0 |
0 |
0 |
|
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 | ||||
|
1 |
Р4 |
0 |
72 |
9 |
9 |
0 |
1 |
-3/2 |
0 |
|
2 |
Р3 |
16 |
24 |
3/4 |
1/2 |
1 |
0 |
1/8 |
0 |
|
3 |
Р6 |
0 |
108 |
11/4 |
3/2 |
0 |
0 |
-3/8 |
1 |
|
4 |
|
|
384 |
3 |
-2 |
0 |
0 |
2 |
0 |
Так как среди чисел
 существует отрицательное значение
существует отрицательное значение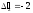 то, следовательно, план
то, следовательно, план не является оптимальным. Разрешимость
задачи остается в силе, так как все
коэффициенты столбца Р2
положительны.
не является оптимальным. Разрешимость
задачи остается в силе, так как все
коэффициенты столбца Р2
положительны.
Разрешающий столбец
 ,
т.к.
,
т.к. .
Этот столбец нужно ввести в базис. Для
определения разрешающей строки найдём
минимумmin
.
Этот столбец нужно ввести в базис. Для
определения разрешающей строки найдём
минимумmin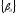 =min
=min =min
=min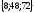 =8.
Следовательно, разрешающая строка
=8.
Следовательно, разрешающая строка
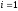 и разрешающий элемент равен
и разрешающий элемент равен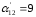 .
.
Первая строка новой симплекс таблицы получается путём деления исходной строки на 9.
|
i |
Базис |
Сб |
βi |
9 |
10 |
16 |
0 |
0 |
0 |
|
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 | ||||
|
1 |
Р2 |
9 |
8 |
1 |
1 |
0 |
1/9 |
-1/6 |
0 |
|
2 |
Р3 |
16 |
20 |
1/4 |
0 |
1 |
-1/18 |
5/24 |
0 |
|
3 |
Р6 |
0 |
96 |
5/4 |
0 |
0 |
-1/6 |
-1/8 |
1 |
|
4 |
|
|
400 |
5 |
0 |
0 |
2/9 |
5/3 |
0 |
Векторы Р2,
Р3
и Р6
образуют базис, соответствующие числа
 равны нулю. Остальные элементы
симплекс-таблицы пересчитываются по
правилу треугольника:
равны нулю. Остальные элементы
симплекс-таблицы пересчитываются по
правилу треугольника:
 =A-BC=24-8*1/2=20
=A-BC=24-8*1/2=20  =108-8*3/2=96
=108-8*3/2=96
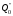 =
=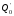 -
- *
*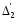 =384-8(-2)=400
=384-8(-2)=400
 =3/4-1/2*1=1/4
=3/4-1/2*1=1/4  =11/4-3/2*1=5/4
=11/4-3/2*1=5/4
 =0-1/2*1/9=-1/18
=0-1/2*1/9=-1/18 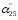 =1/8-1/2*(1/6)=1/8+1/12=5/24
=1/8-1/2*(1/6)=1/8+1/12=5/24
 =3-1(-2)=5
=3-1(-2)=5 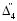 =0-1/9(-2)=2/9
=0-1/9(-2)=2/9
 =2-(-1/6)(-2)=2-1/3=5/3
=2-(-1/6)(-2)=2-1/3=5/3
Так как все
 ,
то полученный план является оптимальным:
,
то полученный план является оптимальным: .
.
Экономическая интерпретация полученного решения: для получения максимальной стоимости нужно произвести 8 изделийВ; 20 изделий С; при этом сырьё I и IIбудет израсходовано полностью, останется 96 кг сырья III. Выпуск продукции в денежном выражении составляет 400 усл. ед.
Задание 2.
Фирма производит три вида продукции (А, В, С), для выпуска каждого из которых требуется определённое время обработки на всех четырёх устройствах I, II, III, IV.
|
Вид продукции |
Время обработки |
Прибыль, дол. | ||||
|
I |
II |
III |
IV | |||
|
А |
1+m |
3 |
1+k |
2 |
3+m | |
|
В |
8-n |
1+n |
3 |
3 |
6+n | |
|
С |
3 |
3 |
2 |
4 |
4+k | |
Пусть время работы на устройствах, соответственно, 84-2m, 42-n, 21+k и 42 часа. В соответствии со своими индивидуальными данными (m – число гласных букв в фамилии студента, n – число гласных букв в полном имени студента, k – число гласных букв в отчестве студента) определите, какую продукцию и в каких количествах следует производить. Рынок сбыта для каждого продукта неограничен. Временем, требуемым для переключения устройства в зависимости от вида продукции, можно пренебречь. Рассмотреть задачу максимизации прибыли.
