- •Санкт-петербургский университет
- •Введение
- •Литература
- •Графический способ решения задачи линейного программирования
- •Симплекс–метод
- •Алгоритм симплекс-метода
- •Транспортная задача. Общие понятия
- •Математическая постановка транспортной задачи
- •Методы нахождения опорного плана
- •1. Метод северо-западного угла
- •2. Метод минимального элемента
- •3. Метод аппроксимации Фогеля
- •Метод потенциалов нахождения оптимального плана транспортной задачи
- •Выбор кратчайшего пути
- •Задача коммивояжера

Санкт-петербургский университет
УПРАВЛЕНИЯ И ЭКОНОМИКИ
Институт экономики, менеджмента и информационных технологий
Кафедра Информационных технологий и математики
Гармашов А.В.
Методическое пособие
для выполнения контрольной работы
по дисциплине
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
на 2014/2015 учебный год
для студентов заочной формы обучения
2014 г.
Методы оптимальных решений. Методическое пособие для выполнения контрольной работы.– СПб.: Изд-во СПбУУЭ, 2014. – 38с.
В пособии рассматриваются важные аспекты дисциплины – «Методы оптимальных решений».
Основными задачами учебного пособия является формирование у студентов базовых знаний по вопросам оптимизации в принятии решений.
Полученные знания позволят будущим специалистам лучше понять специфику развития технологии управления с учетом современных требований.
Учебное пособие предназначено для студентов всех форм обучения высших учебных заведений, обучающихся по специальности «Прикладная информатика».
Составитель: канд. физ-мат. наук А.В. Гармашов
Рецензенты:
Санкт-Петербургский университет управления и экономики
2014 г.
Введение
Самостоятельная работа над учебным материалом является основной формой обучения студента заочного отделения. При этом рекомендуется использовать литературу, перечисленную ниже.
Перед тем как приступить к выполнению контрольных заданий рекомендуется изучить конспект лекций, прочитанных на сессии.
Параметры индивидуального задания определяются тремя числами: m, n и k (числа гласных букв в ФИО студента).
При выполнении контрольных работ следует указать номер задачи и целиком переписать ее условие. Следует выполнить все рисунки, указанные в задании.
Работа должна быть выполнена на стандартных листах формата А4 с одной стороны листа. Каждое задание следует начинать на новом листе.
Листы нумеруются, начиная со второго, и вкладываются в файлы. На титульном листе следует указать индивидуальные данные студента.
Работа, оформленная неверно, рассматриваться не будет.
Литература
И.Л. Акулич "Математическое программирование в примерах и задачах" М., "Лань", 2009.
Исследование операций в экономике: Учебное пособие для вузов: рекомендовано Мин. образования/ Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; Ред. Н. Ш. Кремер. - 2-е изд., перераб. и доп.. - М.: Юрайт, 2011. - 430 с.
Плотников А.Д. Математическое программирование: Экспресс-курс. М.: Новое знание. 2006 г.
В. Круглов, М. Дли, А. Юденков. Математическое программирование в экономике. М.: Финансы и статистика. 2010 г.
К. Балдин, Н. Брызгалов, А. Рукосуев. Математическое программирование. - Издательство: Дашков и Ко. 2009 г.
Моделирование информационных ресурсов: теория и решение задач: учебное пособие для вузов: рекомендовано методсоветом по направлению/ Г. Н. Исаев. М.: ИНФРА-М , 2010. - 224 с.: ил
Графический способ решения задачи линейного программирования
Рассмотрим графический метод решения на следующем примере.
Задача. Для производства двух препаратов A и B химическое производство использует три вида сырья:
|
Виды сырья |
Норма расхода сырья(кг/стандарт) |
Общее количество сырья(кг) | |
|
А |
В | ||
|
I II III |
12 4 3 |
4 4 12 |
300 120 252 |
|
Прибыль от реализации 1 стандарта(усл.ед/станд) |
30 |
40 |
|
Необходимо составить план выпуска, при котором прибыль от реализации выпущенной продукции будет максимальна.
Обозначим х1-количество стандартов препарата А, х2-количество стандартов препарата В.
Целевая функция
(общая прибыль)оптимизируется на максимум
Q=30x1+40x2 max.
max.
По каждому виду сырья составляются ограничения в форме неравенств, а на переменные накладывается условие неотрицательности:

Алгоритм графического решения ЗЛП:
строят прямые линии по условиям-ограничениям;
находят полуплоскости, определяемые каждым ограничением;
находят многоугольник решений (пересечение полуплоскостей);
строят систему параллельных линий Q=const, проходящих через многоугольник;
находят точку, в которой значение целевой функции Q максимально;
определяют оптимальный план (х1*;х2*) и значение целевой функцииQ для оптимального плана.
Решим задачу №1 графически согласно приведенному алгоритму:
- неравенства заменим на равенства
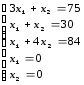
(1)
(2)
(3)
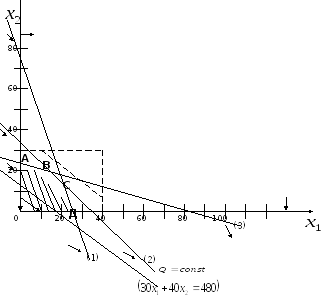
- строим соответствующие прямые;
- определяем полуплоскости по отношению к началу координат О(0;0);
- заштриховываем область пересечения полученных полуплоскостей;
-
строим вектор
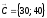 ,
который указывает направление перемещения
прямой
,
который указывает направление перемещения
прямой

-
перемещая прямую
 в
направлении вектора
в
направлении вектора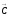 ,
видим, что макс. значение целевая функция
принимает в точке “B”
,
видим, что макс. значение целевая функция
принимает в точке “B”
- определяем координаты точки В, решив систему:
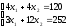
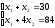
 х*
= (12;18) – оптимальный план.
х*
= (12;18) – оптимальный план.
- максимальная прибыль: Qmax = 30 · 12 + 40 · 18 = 1080 усл.ед.).
Прямая Q=constможет пересекать допустимую область в точке, по лучу, по отрезку. Допустимая область не всегда является ограниченной областью.
Задание 1. Решить задачу с двумя переменными графическим методом в соответствии со своими индивидуальными данными (m – число гласных букв в фамилии студента, n – число гласных букв в полном имени студента, k – число гласных букв в отчестве студента).