Выбор кратчайшего пути

Кроме транспортной задачи, являющейся классической сетевой задачей, можно укажем ещё некоторые задачи на сетях: задача назначений, выбор кратчайшего пути, задача коммивояжера.

Математическая постановка задачи назначений выглядит следующим образом: , где

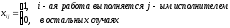
c_ij – сложность выполнения i-ой работы j-ым исполнителем.

Основные особенности данной задачи: число уравнений 2n-1, число переменных n².Так как работы делить нельзя, то из 2n-1 заполненной клетки n клеток содержат «1», а в остальных n-1 клетках содержатся «0», считаясь при этом заполненными. В остальном решение как в случае транспортной задачи.

Рассмотрим более подробно решение задачи выбора кратчайшего пути в сетевой модели.

На рис. изображен пример сетевой модели. Величины c_ijможет выражать длину пути из пункта i в пункт j, стоимость переезда из пункта i в пункт j, время переезда из пункта i в пункт j. При этом, если узлы i и j не связаны друг с другом, то c_ij=.

Таким образом, задача о выборе кратчайшего расстояния является частным случаем задачи о назначениях:

Алгоритм Форда.

Выделяется некоторая вершина, и указываются длины всех дуг. Требуется для любой вершины найти кратчайший путь, ведущий от выделенной вершины к данной или убедиться в том, что не существует путей, ведущих из исходной вершины в данную вершину.

Суть метода Форда заключается в присваивании каждой вершине двойной метки (, x), где  - некоторое число, а x – другая вершина, связанная с данной. В дальнейшем эти метки изменяются.

1. Начальный шаг. Выделенной вершине x₀ присваивается метка (0;x_) и остается неизменной. Каждой из остальных вершин графа присваивается метка (+;x_), которая может меняться.

2. Общий шаг. Поочередно рассматриваются вершины с конечными значениями меток . Вначале имеется лишь одна такая вершина x₀. Выберем вершину x_j, имеющую конечную метку _j. Рассмотрим все дуги x_jx_m, выходящие из вершины x_j и имеющие длину l_jm. Сравниваем имеющиеся уже метки с числом _j+l_jm, где _j+l_jm – сумма метки вершины x_j и длины дуги, ведущей из x_j в x_m. Если _m_j+l_jm, то метка x_m сохраняется. Если _m>_j+l_jm, то вершине x_m присваивается новая метка (_j+l_jm;x_m). Этот шаг прекращается, пока для любой дуги x_jx_m разность меток вершин не будет превосходить длину дуги _m-_jl_jm.

3. Вычисление длины кратчайшего пути. Длина кратчайшего пути из выделенной вершиныx₀ в вершину x_j равна окончательной метке вершины x_j. Если _j=+, то не существует пути из вершины x₀ в x_j.

4. Построение кратчайшего пути. Данное построение осуществляется из x_j путем прохождения через вершины, из которых получена окончательная метка. В обратном направлении полученные вершины и образуют искомый кратчайший путь.

Задача. Построить сеть, заданную следующей таблицей, и найти кратчайшие пути из вершины x₀ в каждую вершину сети.

xixj	0;1	0;2	1;3	1;4	1;6	2;3	2;5	2;6	3;7	4;6	4;8	5;7	6;8	7;6	7;8
lij	10	11	8	23	12	4	6	18	13	9	15	8	13	8	17

Построимсеть данной задачи.

Находим кратчайшие расстояния из вершины x₀. в x_j согласно алгоритму Форда.

1. Начальный шаг. Вершине x₀ присваивается метка (0;x_), остальным метка (+;x_),

2. Общий шаг.

1. Начнем с вершины x₀, имеющей конечную метку ₀=0. Из нее выходят две дуги (0;1) и (0;2). Дуга (0;1) вершине x₁ дает метку ₁=₀+l₀₁=0+10=10. Так как вершина x₁ ещё не имеет меток, то ей присваивается метка (10;x₀). Дуга (0;2) вершине x₂ дает метку ₂=₀+l₀₂=0+11=11, и этой вершине присваивается метка (11; x₀). Так как нет других путей, ведущих в x₁, x₂, то полученные метки будут окончательными.

2. Из вершины x₁ выходят три дуги (1;3), (1;4) и (1;6) к вершинам x₃, x₄ и x₆, не имеющие пока меток. Вычислим метки для этих трех вершин: ₃=₁+l₁₃=10+8=18, ₄=₁+l₁₄=10+23=33 и ₆=₁+l₁₆=10+12=22. Соответствующие вершины будут иметь следующие метки: (18;x₁), (33;x₁)и (22;x₁), причем метка вершины x₄ будет окончательной.

3. Из вершины x₂ выходят три дуги (2;3), (2;5) и (2;6). Вычислим метки для трех вершин x₃, x₅ и x₆: ₃=₂+l₂₃=11+4=15, ₅=₂+l₂₅=11+6=17 и ₆=₂+l₂₆=11+18=29. Соответствующие вершины будут иметь следующие метки: (15;x₂), (17;x₂)и (29; x₂), причем метка вершины x₅ будет окончательной.

Для вершины x₃ имеем прежнюю метку (18;x₁) и новую метку (15;x₂). Так как 15<18, то метка пересматривается и окончательной становится новая метка(15;x₂).

Для вершины x₆ имеем прежнюю метку (22;x₁) и новую метку (29;x₂). Так как 22<29, то оставляем прежнюю метку, причем она не является окончательной.

4. Так как вершина x₃ имеет метку (15;x₂) и из нее выходит единственная дуга (3;7), ведущая в непомеченную вершину x₇, то получаем ₇=₃+l₃₇=15+13=28 и метку (28;x₃), являющейся неокончательной.

5. Вершина x₄ имеет метку (33;x₁) и из нее выходят две дуги (4;6) и (4;8). Вычисляем: ₆=₄+l₄₆=33+9=42, что больше, чем 22 и, следовательно, остается прежняя метка (22; x₁); ₈=₄+l₄₈=33+15=48 и присваивается новая метка (48;x₄).

6. Вершина x₅ имеет метку (17;x₂) и из нее выходит одна дуга (5;7). Вычисляем ₇=₅+l₅₇=17+8=25. Так как предыдущая метка вершины x₇ (28;x₃) больше, то полученная метка (25;x₅) будет окончательной.

7. Из вершины x₆выходит единственная дуга (6;8), для которой ₈=₆+l₆₈=22+13=35. Так как полученная метка (35;x₆) меньше, чем уже имеющаяся (48;x₄), то вершине приписываем метку (35;x₆).

8. Из вершины x₇, имеющей окончательную метку, выходят две дуги (7;6) и (7;8). Вычисляем ₆=₇+l₇₆=25+8=33 и ₈=₇+l₇₈=25+17=42. Так как полученная для x₆ новая метка (33;x₇) больше, чем метка (22; x₁). Для вершины x₈ полученная новая метка(42;x₇) больше имеющейся (35;x₆), то последняя метка будет окончательной.

Окончательно, результаты решения сведем в таблицу.

Вершина	Окончательная метка	Кратчайший путь	Кратчайшее расстояние L0i
x1	(10; x0)	x0→ x1	10
x2	(11; x0)	x0→ x2	11
x3	(15; x2)	x0→ x2→ x3	15
x4	(33; x2)	x0→ x1→ x4	33
x5	(17; x2)	x0→ x2→ x5	17
x6	(22; x2)	x0→ x1→ x6	22
x7	(25; x5)	x0→ x2→ x5→ x7	25
x8	(35; x6)	x0→ x1→ x8	35

Задание 4.

Построить сетевой график, установить кратчайшие пути и найти расстояние от x₁ до всех узлов сети: x₁₂=9; x₁₃=5; x₁₄=5; x₂₉=14-m; x₂₆=4; x₃₂=8; x₃₆=10; x₃₅=8; x₄₃=3+n; x₄₅=4; x₄₈=15-k; x₃₇=3; x₅₈=7; x₆₅=9; x₆₇=3+2k; x₆₉=6; x₇₉=2+m; x_7,10=6;x₈₇=11; x_8,10=12-n; x_9,10=7.