
EMPiV
.pdf
ЭМПиВ
Ответы на экзаменационные вопросы
10.6.2013

Оглавление
|
1. ПРЕДМЕТ КУРСА ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И ВОЛНЫ. ............................................... |
3 |
|
|
2. ВЕКТОРЫ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ........................................................................................................... |
4 |
|
|
Векторы магнитного поля ............................................................................................................................. |
5 |
|
|
3. ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА............................................................................................................. |
7 |
|
|
Второе уравнение Максвелла....................................................................................................................... |
8 |
|
|
Третье и четвертое уравнения Максвелла .................................................................................................. |
9 |
|
|
4. КЛАССИФИКАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ЯВЛЕНИЙ............................................................................. |
11 |
|
|
5. УРАВНЕНИЯ МАКСВЕЛЛА В КОМПЛЕКСНОЙ ФОРМЕ ............................................................................ |
12 |
|
|
6. СТОРОННИЕ ИСТОЧНИКИ. УРАВНЕНИЯ МАКСВЕЛЛА С УЧЕТОМ СТОРОННИХ ИСТОЧНИКОВ........... |
16 |
|
|
УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ МОНОХРОМАТИЧЕСКОГО ПОЛЯ В ОДНОРОДНОЙ |
|
|
|
СРЕДЕ, УЧИТЫВАЮЩИЕ СТОРОННИЕ ИСТОЧНИКИ.................................................................. |
17 |
|
|
7. ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ ...................................................................................... |
18 |
|
|
8. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ. ЗАКОН СОХРАНЕНИЯ ЗАРЯДА. ............................................................ |
19 |
|
|
9. КЛАССИФИКАЦИЯ СРЕД ........................................................................................................................... |
20 |
|
|
10. |
НЕПРИМЕНИМОСТЬ УРАВНЕНИЙ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ НА ГРАНИЦЕ |
|
|
РАЗДЕЛА ДВУХ СРЕД .................................................................................................................................... |
21 |
|
|
11. |
ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ НОРМАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРИЧЕСКОГО И |
|
|
МАГНИТНОГО ПОЛЕЙ .................................................................................................................................. |
22 |
|
|
12. |
ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ КАСАТЕЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРИЧЕСКОГО И |
|
|
МАГНИТНОГО ПОЛЕЙ .................................................................................................................................. |
24 |
|
|
13. |
ГРАНИЧНЫЕ УСЛОВИЯ НА ПОВЕРХНОСТИ ИДЕАЛЬНОГО ПРОВОДНИКА............................... |
28 |
|
14. |
БАЛАНС МГНОВЕННЫХ МОЩНОСТЕЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ОБЪЕМЕ............................. |
31 |
|
15. |
ПОНЯТИЕ О КОМПЛЕКСНОЙ МОЩНОСТИ. БАЛАНС КОМПЛЕКСНЫХ МОЩНОСТЕЙ........................ |
35 |
|
16. |
ВЕКТОР ПОЙНТИНГА. ............................................................................................................................. |
40 |
|
18. |
ВЫВОД ВОЛНОВЫХ УРАВНЕНИЙ ДЛЯ ВЕКТОРОВ Е И Н ...................................................................... |
49 |
|
19. |
ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ............................................................................................ |
50 |
|
20. |
ЭЛЕМЕНТАРНЫЙ ЩЕЛЕВОЙ ИЗЛУЧАТЕЛЬ............................................................................................ |
52 |
|
21. |
МОЩНОСТЬ, ИЗЛУЧАЕМАЯ ЭЛЕМЕНТАРНЫМ ЭЛЕКТРИЧЕСКИМ ИЗЛУЧАТЕЛЕМ. СОПРОТИВЛЕНИЕ |
|
|
ИЗЛУЧЕНИЯ. ЭКВИВАЛЕНТНАЯ СХЕМА ИЗЛУЧАТЕЛЯ................................................................................ |
54 |
|
|
22. |
ПРИНЦИП ПЕРЕСТАНОВОЧНОЙ ДВОЙСТВЕННОСТИ УРАВНЕНИЙ МАКСВЕЛЛА................................ |
56 |
|
23. |
ЭЛЕМЕНТАРНЫЙ МАГНИТНЫЙ ИЗЛУЧАТЕЛЬ ...................................................................................... |
57 |
|
24. |
ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ БЕЗ ПОТЕРЬ............................................. |
63 |
|
25. |
ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ С ПОТЕРЯМИ........................................... |
64 |
|
26. |
МАТЕМАТИЧЕСКАЯ ЗАПИСЬ ВЕКТОРОВ ПОЛЯ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ ПОД |
|
|
УГЛОМ К ОСЯМ КООРДИНАТ ...................................................................................................................... |
66 |
|
|
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН..................................... |
67 |
|
|
ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ С ПРОВОДИМОСТЬЮ ОТЛИЧНОЙ ОТ НУЛЯ. ............................ |
67 |
|
1 |
27. |
ПОЛЯРИЗАЦИЯ ВЕКТОРОВ ПОЛЯ. ВИДЫ ПОЛЯРИЗАЦИИ.......................................... |
72 |

28. |
ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД ПРИ ПАДЕНИИ НОРМАЛЬНО- |
|
ПОЛЯРИЗОВАННОЙ ПЛОСКОЙ ВОЛНЫ. ЗАКОНЫ СНЕЛЛИУСА. КОЭФФИЦИЕНТЫ ФРЕНЕЛЯ. ............... |
74 |
|
30. |
ПОЛНОЕ ПРОХОЖДЕНИЕ ВОЛНЫ ВО ВТОРУЮ СРЕДУ ...................................................................... |
76 |
31. |
ПОЛНОЕ ОТРАЖЕНИЕ ПРИ ПАДЕНИИ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД. |
|
СТРУКТУРА ПОЛЯ. ОСНОВНЫЕ СВОЙСТВА. ПОНЯТИЕ О НАПРАВЛЕННЫХ ВОЛНАХ. ВОЛНЫ ТИПА Н И |
||
Е. .................................................................................................................................................................... |
|
78 |
32. |
ПАДЕНИЕ ПЛОСКОЙ ВОЛНЫ НА ПОВЕРХНОСТЬ ИДЕАЛЬНОГО МЕТАЛЛА ........................................ |
81 |
33. |
ПРИНЦИП ДЕЙСТВИЯ ДИЭЛЕКТРИЧЕСКОГО И МЕТАЛЛИЧЕСКОГО ВОЛНОВОДОВ. ......................... |
82 |
34. |
ПАДЕНИЕ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ ПОГЛОЩАЮЩЕЙ СРЕДЫ ................................................ |
83 |
35. |
ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ ЛЕОНТОВИЧА-ЩУКИНА..................................................... |
85 |
36. |
ПОТЕРИ ЭНЕРГИИ В ПРОВОДНИКЕ. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ МОЩНОСТИ ДЖОУЛЕВСКИХ ПОТЕРЬ |
|
В ПРОВОДНИКАХ. ......................................................................................................................................... |
87 |
|
37. |
МЕТОДЫ СНИЖЕНИЯ ТЕПЛОВЫХ ПОТЕРЬ В ПРОВОДНИКАХ.............................................................. |
89 |
39. |
АНАЛИЗ ОДНОРОДНОЙ ЛИНИИ ПЕРЕДАЧИ. СВЯЗЬ ПРОДОЛЬНЫХ И ПОПЕРЕЧНЫХ |
|
СОСТАВЛЯЮЩИХ ТАКОЙ ВОЛНЫ. .............................................................................................................. |
98 |
|
40. |
РЕЖИМЫ РАБОТЫ ОДНОРОДНОЙ ЛИНИИ ПЕРЕДАЧИ. КРИТИЧЕСКАЯ ЧАСТОТА. ДЛИНА ВОЛНЫ |
|
ЛИНИИ. ФАЗОВАЯ СКОРОСТЬ ВОЛНЫ ........................................................................................................ |
98 |
|
41. |
ВОЛНЫ ТИПА Н В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ. КЛАССИФИКАЦИЯ, ОСНОВНЫЕ СВОЙСТВА. 103 |
|
42.СТРУКТУРА ПОЛЕЙ ВОЛН ТИПА Н10, Н01, Н11 ................................................................................... |
104 |
|
43. |
ВОЛНЫ ТИПА Е В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ........................................................................... |
106 |
44. |
СТРУКТУРА ПОВЕЙ ВОЛНЫ ТИПА Е11, СТРУКТУРА ТОКОВ ПРОВОДИМОСТИ. ................................ |
115 |
45. |
ОДНОВОЛНОВЫЙ И МНОГОВОЛНОВЫЙ РЕЖИМЫ РАБОТЫ ВОЛНОВОДА. ................................... |
116 |
2

1. ПРЕДМЕТ КУРСА ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И
ВОЛНЫ.
Предмет изучения - электромагнитные поля и волны, закономерности их возбуждения и распространения, канализирующие и резонансные системы СВЧ. Задачи изучения дисциплины состоят в уяснении основных явлений физики электромагнитного поля и усвоении понятий и закономерностей электродинамики.
3
2. ВЕКТОРЫ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
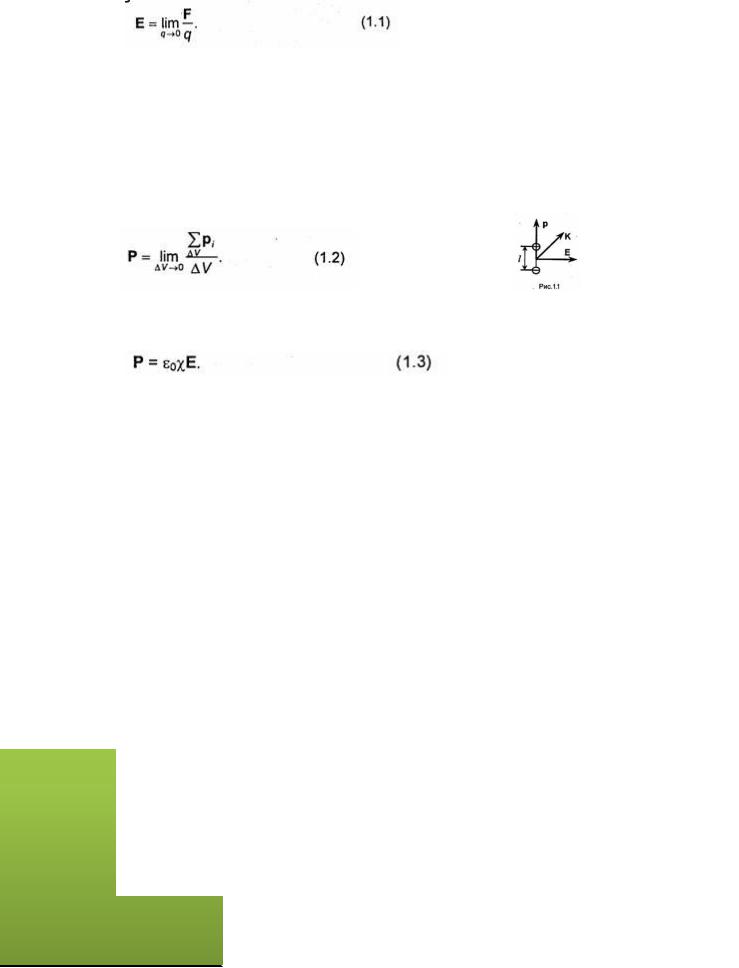
Напряженность электрического поля Е определяют как силу, с которой электрическое поле действует на точечный положительный единичный заряд: Е = F/q. Заряд q должен быть достаточно малым, чтобы можно было пренебречь изменением распределения зарядов, создающих исследуемое поле. Поэтому
Символ q →0 означает, что уменьшается величина заряда и размеры объекта, на котором распределен заряд.
В системе СИ [Е] = Н/Кл = В∙А∙с/(м∙А∙с) = В/м.
Физически смысл: Под действием электрического поля вещество поляризуется. В результате появляется дополнительное электрическое поле, которое налагается на первичное. При этом суммарное электрическое поле оказывается отличным от того, каким оно было бы в вакууме.
Вектор поляризованности Р-предел отношения суммарного дипольного момента вещества в объеме V к величине этого объема при V→0:
Вектор P (Кл/м2).
При не очень сильном внешнем поле величину индуцированного дипольного момента можно считать пропорциональной напряженности электрического поля:
χ- диэлектрическая восприимчивость среды, характеризует средубезразмерный.
Постоянный коэффициент ε 0 - электрической постоянной. В системе СИ ε 0 = |
|
10-9/(36π), [Ф/M]. |
|
D = ε 0E + P. |
(1.4) |
С учетом (1.3) формулу (1.4) можно представить в виде |
|
D = ε E, |
(1.5) |
где ε = ε о(1+χ) .Вектор D -векторэлектрической индукции, а параметр ε - абсолютной диэлектрической проницаемостью среды. D (Кл/м2) Так как диэлектрическая восприимчивость вакуума равнанулю(χ= 0), то электрическую постоянную ε 0 можно рассматривать как абсолютную диэлектрическую проницаемость вакуума(Ф/м). Относительная диэлектрическая проницаемость среды ε r,ε =ε0 εr (1.6)ε r=1+ χ
Рассмотрим электрическое поле, создаваемое точечным зарядом Q, расположенным в безграничной среде, где ε -скалярная постоянная (ε = const). Среда однородная и изотропная по отношению к электрическому полю. Согласно закону Кулона сила, с которой точечный заряд Q в рассматриваемом
случае действует на точечный заряд q,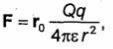
где r- расстояние между зарядами Q и q, а r0-единичный вектор, направленный вдоль Q к q (рис. 1.2). 1.1 Следует, что напряженность электрического поля,
создаваемого точечным зарядом Q,  Переходя к вектору D на основе равенства (1.5), замечаем, что вектор D в однородных изотропных средах не зависит от ε.Следовательно, при ε = const и одинаковом распределении свободных зарядов вектор D имеет одинаковые
Переходя к вектору D на основе равенства (1.5), замечаем, что вектор D в однородных изотропных средах не зависит от ε.Следовательно, при ε = const и одинаковом распределении свободных зарядов вектор D имеет одинаковые
4 значения в разных средах, т.е. не зависит от "связанных" зарядов вещества. Под действием электрического поля в среде, обладающей проводимостью,
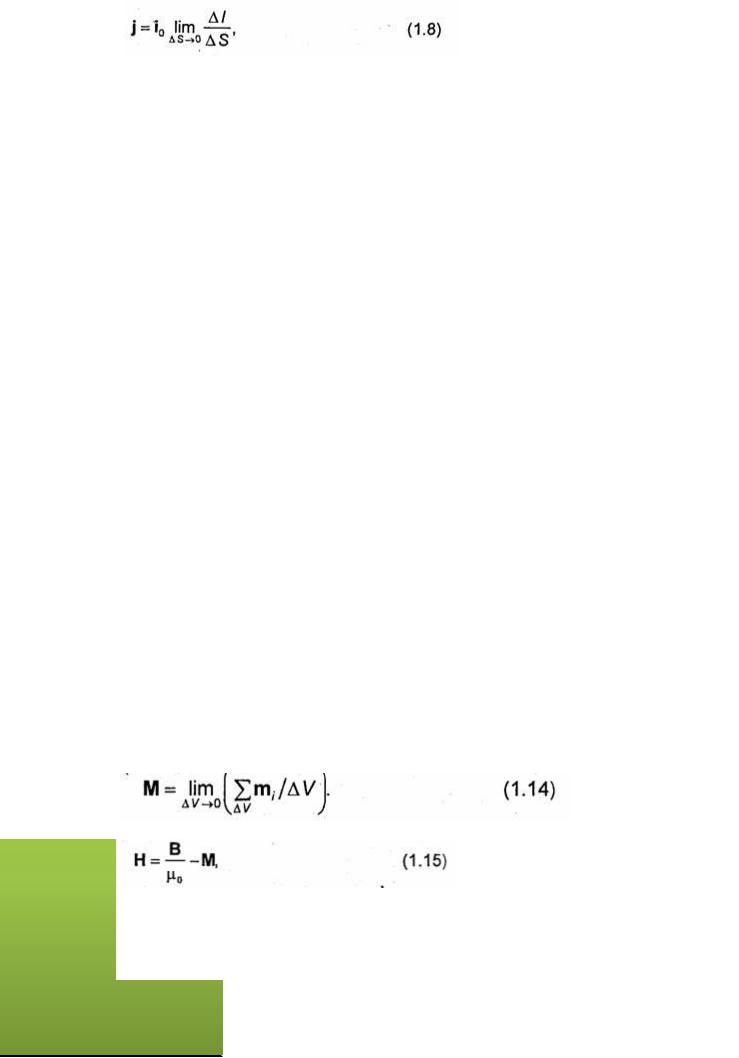
возникает электрический ток (ток проводимости), распределение которого удобно характеризовать вектором плотности тока проводимости
где i0-единичный вектор, показывающий направление тока (направление движения положительных зарядов) в рассматриваемой точке М; S-плоская площадка, содержащая точку М, расположенная перпендикулярно вектору i0, а Δ/-ток проводимости, протекающий через ∆S. Вектор j также вектором объемной плотности тока проводимости. Как видно из (1.8), вектор j (А/м 2).
Вектор j связан с вектором Е соотношениемj = ζE, |
(1.9) |
-закон Ома в дифференциальной форме. Коэффициент пропорциональности ζ -
удельная проводимость среды (См/м).
Векторы магнитного поля
Сила, с которой электромагнитное поле воздействует наточечный электрический заряд, зависит не только от местоположения и величины заряда, но и от скорости его движения. Эту силу обычно раскладывают на две: электрическую и магнитную.
Электрическая сила не зависит от движения заряда:Fэ = qE. |
(1.10) |
Магнитная сила FM зависит от величины и направления скорости v движения
заряда и всегда перпендикулярна ей:FM = q[v, В]. |
(1.11) |
В-вектор магнитной индукции, характеризующий силовое воздействие магнитного поля. Магнитная индукция численно равна силе, с которой магнитное поле действует на единичный точечный положительный заряд, движущийся с единичной скоростью перпендикулярно линиям вектора В (Тл) или (Вб/м2).
Размерность следует, из (1.11): [В] = [F]/([q] [v]) = Нс/(Клм) = (В∙А∙с2/м)/(А∙с∙м) = В∙с/м2 = Вб/м2 = Тл.
Полная сила, действующая на точечный заряд q, находящийся в |
|
|
электромагнитном поле (лоренцова сила),F = qE + q[v, В]. |
(1.12) |
|
Магнитное поле действует, конечно, не только на отдельные движущиеся |
|
|
заряды, но и на проводники, по которым течет электрический ток. Например, |
||
сила F, с которой однородное магнитное поле действует на прямолинейный |
||
проводник длиной I с током /, определяется экспериментально установленным |
||
законом |
|
|
F = /l[lo,B], |
(1.13) |
|
где lo-единичный вектор, направление которого совпадает с направлением тока, т.е. с направлением движения положительных зарядов в проводнике. Отметим, что формула (1.13) является следствием формулы (1.11).
Намагниченность среды характеризуется вектором намагниченности М, который определяют как предел отношения суммарного магнитного момента вещества в объеме V к величине этого объема при \/→0:
Вектор М (А/м).
где μ0- магнитной постоянной μ0 = 4-10-7 Гн/м.
Вектор Н - вектор напряженности магнитного поля (А/м).
При не очень сильном внешнем магнитном поле можно считать, что
5 |
вектор М пропорционален вектору В. В силу линейности уравнения (1.15) можно |
|
также считать пропорциональными векторы М и Н: |
||
|

Безразмерный коэффициент χт- магнитная восприимчивостью среды. Подставляя формулу (1.16) в (1.15), получаем
где |
Коэффициент пропорциональности р. между В и Н - |
абсолютная магнитной проницаемостью среды(Гн/м). Магнитная |
|
восприимчивость вакуума считается равной нулю, поэтому магнитную |
|
постоянную μ0 |
можно рассматривать как абсолютную магнитную проницаемость |
вакуума. |
|
Наряду с абсолютной магнитной проницаемостью среды р вводят
также относительную магнитную проницаемость μr
Очевидно, что 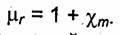 Отметим важное свойство вектора Н. В средах, в которых μ -скалярная
Отметим важное свойство вектора Н. В средах, в которых μ -скалярная
постоянная (однородными и изотропными по отношению к магнитному полю), вектор Н не зависит от μ. Поэтому при одинаковых источниках магнитного поля значения вектора Н в разных однородных изотропных средах будут одинаковы.
6

3. ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА
Векторы электрического поля Е, Р, D связаны соотношением (1.4), а векторы магнитного поля В, М, Н-соотношением (1.15), то для определения электромагнитного поля векторы Е, D, В и Н. В линейных изотропных средах, для которых справедливы соотношения (1.5) и (1.17), электромагнитное поле полностью определено двумя векторами ( Е и Н).
Первое уравнение Максвелла является обобщением закона полного тока (закона Ампера).
Таким образом, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля - тока смещения. Плотность тока смещения определяется формулой
в А/м2.
Подчеркнем, что ток проводимости и ток смещения в вакууме имеют различную физическую сущность. Ток проводимости -это упорядоченное движение свободных электрических зарядов. Ток смещения в вакууме соответствует изменению электрического поля и не сопровождается каким-либо движением электрических зарядов. В вакууме D = е0Е И уравнение (1.28) принимает
вид 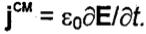 Ток смещения в вакууме не сопровождается выделением тепла.
Ток смещения в вакууме не сопровождается выделением тепла.
Рассмотрим общий случай, когда ток смещения возникает в какой-либо среде. Вектор электрического смещения связан с векторами Е и Р соотношением (1.4). Подставляя это соотношение в (1.28), получаем
Первое слагаемое в правой части этой формулы совпадает с выражением для плотности тока смещения в вакууме, т.е. определяет как бы "чистый" ток смещения, не связанный непосредственно с движением зарядов. Второе слагаемое определяет ток смещения, обусловленный движением зарядов, связанных с атомами вещества, в результате действия переменного поля. Эту составляющую тока смещения можно рассматривать как своеобразный ток проводимости, так как она, по существу, обусловлена упорядоченным перемещением связанных зарядов. На ее поддержание в реальной среде затрачивается некоторая часть энергии электромагнитного поля.
Максвелл предположил, что уравнение (1.25) имеет частный характер, так как не учитывает токов смещения. Для того чтобы оно было справедливым и в случае переменных полей, нужно в его правую часть помимо тока проводимости / ввести ток смещения /см:
7

Уравнение (1.31) применительно к контуру конечных размеров. Оно представляет собой первое уравнение Максвелла в интегральной форме.
Для перехода к дифференциальной форме воспользуемся теоремой Стокса (П.20). Заменяя в уравнении (1.31) циркуляцию вектора Н интегралом от rot H по поверхности S, получаем
Так как S-произвольная поверхность, то равенство (1.32) возможно только в том
случае, если  Равенство (1.33) называют первым уравнением Максвелла. Векторное уравнение
Равенство (1.33) называют первым уравнением Максвелла. Векторное уравнение
(1.33) эквивалентно трем скалярным уравнениям, которые в декартовой системе
координат х, у, z имеют вид
Второе уравнение Максвелла
Второе уравнение Максвелла является обобщением закона индукции Фарадея, который формулируется: если замкнутый контур Г пронизывается переменным магнитным потоком Ф, то в контуре возникает ЭДС, равная скорости изменения
этого потока:  Знак минус в правой части формулы (1.34) означает, что возникающая в контуре ЭДС всегда как бы стремится воспрепятствовать изменению потока, пронизывающего данный контур"правило Ленца".
Знак минус в правой части формулы (1.34) означает, что возникающая в контуре ЭДС всегда как бы стремится воспрепятствовать изменению потока, пронизывающего данный контур"правило Ленца".
Максвелл предположил, что это уравнение будет справедливо и в том случае, когда рассматриваемый контур представляет собой замкнутую линию, проведенную в непроводящей среде.
Электродвижущая сила, наводимая в этом контуре
а магнитный поток Ф связан с вектором В соотношением
где dS = nodS; п0-орт нормали к поверхности S, образующий правовинтовую систему с обходом контура Г (рис.1.6). Подставляя (1.35) и (1.36) в (1.34),
получаем 
второе уравнение Максвелла в интегральной формедля контура конечных размеров. Максвеллом это уравнение было сформулировано также в дифференциальной форме.
8 Предположим, что контур Г неподвижен и не изменяется со временем. В этом случае производную по времени в правой части уравнения (1.37) можно внести

под знак интеграла. Преобразовывая левую часть равенства (1.37) по теореме
Стокса, имеем 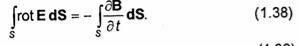
Так как S-произвольная поверхность, соотношение (1.38) возможно только в том
случае, если Равенство (1.38) называют вторым уравнением Максвелла. Переходя к
декартовой системе координат х, у, z, получаем три скалярных уравнения:
Третье и четвертое уравнения Максвелла
Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядомQ, сосредоточенным внутри этой поверхности:
где dS = nodS; n0 - орт внешней нормали к поверхности S.
Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в
общем случае 
где ρ-объемная плотность зарядов; V- объем, ограниченный поверхностью S. Объемная плотность зарядов
где ΔQ - заряд, сосредоточенный в объеме ΔV. Размерность (Кл/м3). Подставляя (1.41) в (1.40), получаем
-третье уравнение Максвелла в интегральной форме. Для перехода к диффе-
ренциальной форме преобразуем левую часть этого уравнения по теореме
Остроградскогo—Гаусса (П. 19) 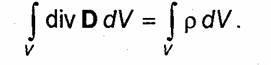
Это равенство должно выполняться при произвольном объеме V, что возможно в случае, если 
9 |
Соотношение (1.44) принято называть третьим уравнением Максвелла. В |
|
декартовой системе координат оно записывается в виде |
||
|
