EMPiV
.pdf
19. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
Для нахождения векторов поля по заданным источникам сторонних зарядов или токов используется волновые уравнения, но они имеют сложную правую часть, поэтому нахождение векторов поля затруднительно. Для упрощения анализа используют вспомогательные функции – электродинамические потенциалы.
Согласно 4 уравнению Максвелла
Из высшей математики известно, что
Это означает, что вектор 
является ротором какого-либо элемента.
Согласно 2 уравнению Максвелла
Известно, что 
Значит,
– векторный электродинамический потенциал, u – скалярный электродинамический потенциал.
Подставим полученные выражения 3,2 и 3,4 в первое уравнение Максвелла:
50 
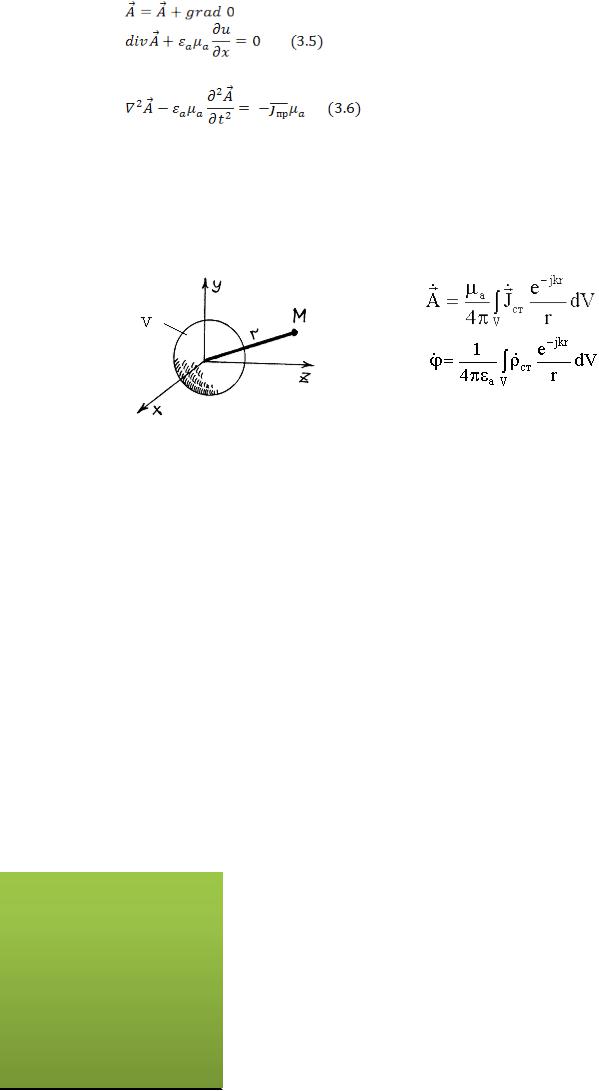
Уравнение 3,5 называют условием калибровки Лоренца.
Уравнение 3.6 достаточно просто позволяет при заданных источниках найти вспомогательный параметр 
.
Опуская ввиду громоздкости строгий вывод решения неоднородных дифференциальных уравнений (4.9) и (4.10), приведем лишь конечный
результат решения этих уравнений:
(3.8)
(3.9)
– область пространства, содержащая сторонние источники;
r – расстояние от источника до точки наблюдения.
51
20. ЭЛЕМЕНТАРНЫЙ ЩЕЛЕВОЙ ИЗЛУЧАТЕЛЬ
Рассмотрим бесконечно протяженную идеально проводящую плоскость, по которой текут поверхностные электрические токи с плотностью js. Если в такой плоскости перпендикулярно jsпрорезать узкую щель, то эта щель пересечет линии вектора js(рис. 5.21), а на ее краях линии тока проводимости будут преобразовываться в линии тока смещения, т.е. в области щели касательная составляющая вектора Ё будет отлична от нуля: Ёηm = E0. Предположим, что длина щели l много меньше длины
волны, а значения амплитуды и фазы Ёоне изменяются по всей длине щели (E0 = const). Описанную систему будем называть элементарным щелевым излучателем или элементарным щелевым вибратором.
Вслучае реальной щели условие Ёо = const не выполняется. Выровнять распределение Eηm вдоль щели можно, если конфигурацию щели сделать аналогичной вибратору Герца (рис. 5.22).
Элементарным щелевым вибратором является также достаточно малый элемент щелевого вибратора конечных размеров.
Вобласти щели имеется касательная составляющая напряженности
электрического поля и отсутствует касательная составляющая напряженности магнитного поля. Последнее следует, например, из того, что любое распределение поверхностных токов, текущих по плоскому экрану, создает вне его магнитное поле, имеющее в плоскости экрана только нормальную составляющую вектора Н. Таким образом, в щели выполняются такие же условия, как на поверхности элементарного магнитного вибратора. Отличие состоит только в том, что электрические силовые линии на поверхности ЭМВ являются замкнутыми (см. рис. 5.17), а в случае щели они оканчиваются на ее краях. Аналогичными будут и структуры полей, создаваемые ЭМВ и элементарным щелевым излучателем. Предположим для простоты, что ЭМВ представляет собой узкую бесконечно тонкую плоскую пластинку, выполненную из материала с бесконечно большой магнитной проницаемостью. Пластинка и щель имеют одинаковую конфигурацию, а значения составляющей Eηm на них совпадают и равны E0. Вообразим теперь бесконечную плоскость Q, проходящую через плоскость ЭМВ (рис. 5.23, а). СоставляющаяЁηm на этой плоскости обращается в нуль всюду, кроме участка, занимаемого ЭМВ, где она равна Ео. На плоскости, в которой прорезана щель, выполняются такие же краевые условия: в области щели Ё ηm= E0, на остальной части Eηm= 0. При рассмотрении поля в одном полупространстве можно считать, что металлическая плоскость в случае щелевого вибратора и воображаемая плоскость Q являются замкнутыми, предполагая, что они замыкаются в бесконечности. При этом
52
краевые условия получаются заданными на замкнутых поверхностях. Одинаковым краевым условиям на одинаковых замкнутых поверхностях соответствуют одинаковые поля во всем рассматриваемом пространстве. Поэтому можно утверждать, что поле, создаваемое в каждом полупространстве элементарным щелевым вибратором (см. рис. 5.23, б), будет таким же, как поле, создаваемое ЭМВ. В частности, в пространстве над плоскостью со щелью поле, создаваемое элементарным щелевым излучателем, будет определяться формулами (5.20), в которых надо считать iM=LE0, где L-периметр ЭМВ, равный 2а (а-ширина щели). Подставляя в (5.10)iм =2аЁ0, получаем
53
21. МОЩНОСТЬ, ИЗЛУЧАЕМАЯ ЭЛЕМЕНТАРНЫМ ЭЛЕКТРИЧЕСКИМ ИЗЛУЧАТЕЛЕМ. СОПРОТИВЛЕНИЕ ИЗЛУЧЕНИЯ. ЭКВИВАЛЕНТНАЯ СХЕМА ИЗЛУЧАТЕЛЯ.
54
55
22. ПРИНЦИП ПЕРЕСТАНОВОЧНОЙ ДВОЙСТВЕННОСТИ УРАВНЕНИЙ МАКСВЕЛЛА.
= + ст
= − − м
(1)
Рассмотрим систему уравнений Максвелла для монохроматического поля (1)
Если в этих уравнениях формально заменить
на и на |
|
на − и на − |
(2) |
ст на −м и м на −ст
то первое уравнение системы (1) превратится во второе, а второе -в первое. В целом система уравнений (1) не изменится. Эту особенность уравнений (1) называют перестановочной двойственностью уравнений Максвелла.
Из перестановочной двойственности уравнений Максвелла вытекает важное следствие. Пусть две краевые электродинамические задачи сформулированы для геометрически одинаковых областей таким образом, что все условия, которым должны удовлетворять векторы Eи Н в первой задаче, при заменах (2)переходят соответственно в условия для векторов Н и Ё второй задачи. Иными словами, при заменах (2) первая задача превращается во вторую, а вторая -в первую. Тогда нет необходимости решать обе задачи, достаточно найти решение одной из них. Произведя в найденном решении замены (2), получим решение другой задачи.
56
23. ЭЛЕМЕНТАРНЫЙ МАГНИТНЫЙ ИЗЛУЧАТЕЛЬ
По аналогии с элементарным электрическим вибратором систему, эквивалентную короткому по сравнению с длиной волны элементу магнитного тока, амплитуда и фаза которого одинаковы во всех точках этого элемента, будем называть элементарным магнитным вибратором. Рассмотрим некоторые физические модели элементарного магнитного вибратора. Для этого вначале вернемся к элементарному электрическому вибратору.
Как уже отмечалось, одной из возможных моделей ЭЭВ является элемент прямолинейного провода (рис. 5.16). Для простоты изложения будем считать провод идеально проводящим. Тогда протекающий по вибратору ток окажется поверхностным с
плотностью js=iст/L, где L - периметр провода.
На поверхности S вибратора касательная составляющая вектора Н неизменна вдоль его длины и связана с плотностью токаjsсоотношением js=[n0,H]|s. Комплексная амплитуда -электрического тока, обтекающего ЭЭВ, равна
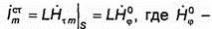комплексная амплитуда составляющей Hθ. На вибраторе линии вектора Н перпендикулярны линиям вектора j и имеют вид колец, охватывающих вибратор (рис. 5.16).
Таким образом, ЭЭВ можно представить в виде стержня, на поверхности которого задано распределение касательной составляющей вектора Н. На концах вибратора ток проводимости переходит в ток смещения, которому соответствуют выходящие из торцов электрические силовые линии (рис. 5.16). Так как ток в ЭЭВ однозначно связан с касательной составляющей напряженности магнитного поля на его поверхности, то поле в пространстве
вокруг вибратора можно выразить через значение 
.
|
Рассмотрим теперь систему, аналогичную описанной модели ЭЭВ, но |
|
|
отличающуюся от нее тем, что на поверхности стержня выполняется иное |
|
|
граничное условие, а именно каса-тельная составляющая вектора Ё отлична от |
|
|
нуля и неизменна вдоль длины l, причем линии вектора Ё имеют вид колец, |
|
|
охватывающих поверхность S (рис. 5.17). Иными сло-вами, данная система |
|
|
отличается от рассмотренной тем, что на поверхности S вместо замкнутых |
|
|
векторных линий магнитного поля задано распределение замкнутых линий |
|
|
электрического поля. Векторные линии магнитного поля второй системы |
|
|
совпадают по форме с векторными линиями электрического поля первой |
|
|
системы, но имеют противоположное направление. Различное направление |
|
|
магнитных и электрических линий системы следует из уравнений Максвелла |
|
|
(правые части первого и второго уравнений (1.75) имеют разные знаки). Задание |
|
|
касательной составляющей вектора Ё на поверхности стержня эквивалентно |
|
57 |
заданию плотности поверхностного магнитного тока |
|
Так как по предположению значения Eθmодинаковы во всех точках поверхности |
||
|
S, то рассматриваемая система эквивалентна элементу длиной (. магнитного тока iм, т.е. представляет собой элементарный магнитный вибратор. Практически систему, близкую к данной модели элементарного магнитного вибратора, можно получить, если стержень выполнить из материала с магнитной проницаемостью μ2. значительно большей магнитной проницаемости μ окружающей среды, например из феррита. В качестве возбуждающего устройства можно использовать рамку, обтекаемую током проводимости (рис. 5.18). Рамка и стержень должны иметь общую ось.
Благодаря большой величине μr2 поток линий вектораВпронизывает стержень, почти не ответвляясь через его боковую поверхность, т.е. поток линий вектора В равномерен по длине стержня. Пронизывающим стержень линиям вектораВсоответствуют
ветотвуют замкнутые линии вектора Е. Равномерность потока вектора В обусловливает равномерное распределение Еθ на поверхности магнитного вибратора. Практически для того, чтобы распределение Eθ на поверхности магнитного вибратора было действительно равномерным, нужно аналогично тому, как это было сделано Герцем в случае электричес-кого вибратора, использовать стержни с шарами или другими концевыми нагрузками (рис. 5.18). Элементарным магнитным вибратором можно считать также любой достаточно малый элемент длинного стержня, выполненного из соответствующего материала и воз-бужденного таким образом, что на его поверхности имеется отличная от нуля перпендикулярная оси стержня касательная составляющая напряженности электрического поля (Ёθs ≠ 0), а другие составляющие вектора Е отсутствуют.
Следует отметить, что аналогия между физическими моделями элементарных электрического и магнитного вибраторов проявляется не только в распределении Нθ на электрическом иЕθна магнитном вибраторах. Благодаря высокой проводимости ма-териала электрического вибратора, на его поверхности выполняется условиеЁηIs→ 0. Точно так же при μr2»μr1 на поверхности магнитного вибратора Нr|s→ 0. Это следует из второго уравнения
Максвелла 
и условия непрерывности касательной
|
составляющей вектора Н на границе раздела двух сред. |
|
|
Если в схеме, изображенной на рис. 5.18, изъять стержень, оставив одну рамку, |
|
|
то характер структуры поля не изменится (рис. 5.19). Поэтому рамку достаточно |
|
|
малых размеров, обтекаемую электрическим током, также можно считать |
|
|
элементарным магнитным вибратором. |
|
|
Поле |
|
58 |
Выражения для комплексных амплитуд составляющих векторов поля, |
|
создаваемого элементарным магнитным вибратором, могут быть получены из |
||
|
формул (5.3), (5.4) и (5.5) для поля ЭЭВ, в которых нужно только в соответствии с принципом двойственности
заменить на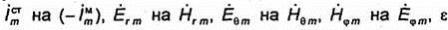 
(-μ) и μ на (-ε).
Окончательные выражения очевидны, и мы не будем их здесь выписывать. Из формул для поля элементарного магнитного вибратора следует, что вектор Ё имеет одну составляющуюЁθ, а вектор Н-две составляющие НrиH θт.е.
вектор Ё в этом случае лежит в азимутальных плоскостях, а вектор, Н - в меридиональных.
Подчеркнем, что найденные таким образом формулы соответствуют магнитному
току, который при нулевой начальной фазе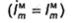 
в момент времени t=0 течет в направлении, противоположном полярной оси системы координат r, θ, θт.е. в направлении (-z0).
Как и в случае ЭЭВ, в выражениях для поля элементарного магнитного вибратора (ЭМВ) имеются слагаемые, пропорциональные 1/(kr) в первой, второй и третьей степенях.
Поэтому при анализе структуры поля элементарного магнитного вибратора окружающее его пространство также удобно разделить на три зоны: ближнюю (kr<<1), дальнюю (kr>>1) и промежуточную, где krсоизмеримо с единицей.
Ограничимся анализом дальней зоны. Поступая так же, как и в случае элементарного электрического вибратора, получаем
Из формул (5.20) следует, что поле, создаваемое ЭМВ в дальней зоне, представляет собой неоднородную поперечную сферическую.волну, распространяющуюся от вибратора со скоростью света. Векторы Е и Н изменяются синфазно. На рис.5.20 показана ориентация векторов ЕиНв дальней зоне в случае ЭЭВ (рис. 5.20, а) и элементарного магнитного вибратора (рис. 5.20, б).
59