
EMPiV
.pdf
 Распространение электромагнитной волны сопровождается переносом энергии. Энергия распространяется со скоростью света перпендикулярно поверхностями равных фаз, т.е. фазовая скорость и скорость распространения энергии совпадают. Отношение амплитуд напряженностей электрического и магнитного полей
Распространение электромагнитной волны сопровождается переносом энергии. Энергия распространяется со скоростью света перпендикулярно поверхностями равных фаз, т.е. фазовая скорость и скорость распространения энергии совпадают. Отношение амплитуд напряженностей электрического и магнитного полей
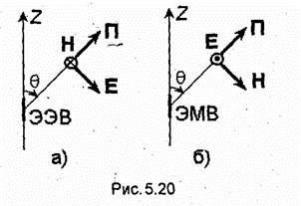
Kак и элементарный электрический виоратор, элементарный магнитный вибратор обладает направленными свойствами. Его излучение максимально в
экваториальной плоскости 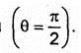
Вдоль своей оси (оси Z) элементарный магнитный вибратор не излучает. Диаграммы направленности элементарного магнитного вибратора совпадают с диаграммами направленности элементарного электрического вибратора (рис.
5.11-5.15).
Как уже отмечалось, достаточно малая рамка (виток провода), обтекаемая постоянным по амплитуде электрическим током /р = = /pmcos(ωt + ψ1), где ψ1начальная фаза тока, также может рассматриваться как элементарный магнитный вибратор. В этом случае вибратор характеризуется амплитудой тока (/р) и площадью рамки S. Формулы для поля, создаваемого рамкой, могут быть получены независимо от формул для поля элементарного электрического вибратора. Для этого нужно записать выражение для векторного потенциала кольцевого электрического токаА, вычислить входящий в
это выражение интеграл в предположении, что расстояние от рамки до точки наблюдения велико по сравнению с размерами рамки, а затем перейти к векторам Ё и Н, как это было сделано в случае элементарного электрического вибратора. Сравнение
окончательных выражений для поля, создаваемого рамкой, с формулами для поля элементарного магнитного вибратора показывает, что они переходят друг в друга при замене вида
60

Длину ЭЭВ, при которой в случае одинаковых токов, обтекающих рамку и вибратор 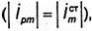 мощность излучения ЭЭВ равна мощности излучения
мощность излучения ЭЭВ равна мощности излучения
рамки, называют действующей высотой 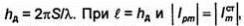 как видно той рамки. Она равна и из формул (5.22) и (5.6), рамка создает в дальней зоне такие же по величине (но не по ориентации векторов электрическое и магнитное поля, как и элементарный электрический вибратор.
как видно той рамки. Она равна и из формул (5.22) и (5.6), рамка создает в дальней зоне такие же по величине (но не по ориентации векторов электрическое и магнитное поля, как и элементарный электрический вибратор.
Полученные выше результаты позволяют также выписать формулы для поля, создаваемого элементарным магнитным вибратором в виде короткого по сравнению с длиной волны стержня из материала с μr2>>1. на боковой поверхности которого задано распределение касательной составляющей вектора E(Eηm |S=E°θ = const). Для этого достаточно в формулах для поля элементарного магнитного вибратора в виде элемента магнитного тока заменить
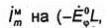 L - периметр поперечного сечения стержня).
L - периметр поперечного сечения стержня).
61

6.1.2. Свойства плоской волны в однородной изотропной среде
Рассматривая таким же образом фазу напряженности электрического поля волны 2), придем к равенству ωΔt=-βΔz. В этом случае положительным t соответствуют отрицательные значения Δz, то есть волна 2) распространяется противоположно оси Z.
62

24. ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ БЕЗ ПОТЕРЬ
Векторы поля
Основные свойства
ВектрыE и H перпендикулярны друг другу и направлению распространения волны (оси Z), т.е. волна является поперечной. Поверхности равных фаз определяются уравнением z=const и представляют собой плоскости перпендикулярные оси Z. Амплитуды векторов E и H экспоненциально убывают (возрастают) вдоль оси Z, что определяется множителем − . Поверхности равных амплитуд совпадают с поверхностями равных фаз. Волны обладающие таким свойством, как и волны, амплитуды векторов Е и Н которых не зависят от координат, называют однородными
Фазовая скорость
Характеристическое сопротивление
Длина волны
63

25. ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ С ПОТЕРЯМИ
Векторы поля
Основные свойства
ВектрыE и H перпендикулярны друг другу и направлению распространения волны (оси Z), т.е. волна является поперечной. Поверхности равных фаз определяются уравнением z=const и представляют собой плоскости перпендикулярные оси Z. Амплитуды векторов E и H экспоненциально убывают (возрастают) вдоль оси Z, что определяется множителем − . Поверхности равных амплитуд совпадают с поверхностями равных фаз. Волны обладающие таким свойством, как и волны, амплитуды векторов Е и Н которых не зависят от координат, называют однородными
Вывод формул для коэффициентов распространения и затухания.
64

Понятие дисперсии
(от лат. dispersio — рассеяние), зависимость фазовой скорости vфгармонич. волны от еѐ частоты w. Простейшим примером явл. Д. в. в линейных однородных средах, характеризуемая т. н. дисперс. уравнением (законом дисперсии); оно связывает частоту и волн.число k плоской гармонич. волны: w=w(k) (а в анизотропных средах — частоту и волн. вектор k).
65

26. МАТЕМАТИЧЕСКАЯ ЗАПИСЬ ВЕКТОРОВ ПОЛЯ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ ПОД УГЛОМ К ОСЯМ КООРДИНАТ
66
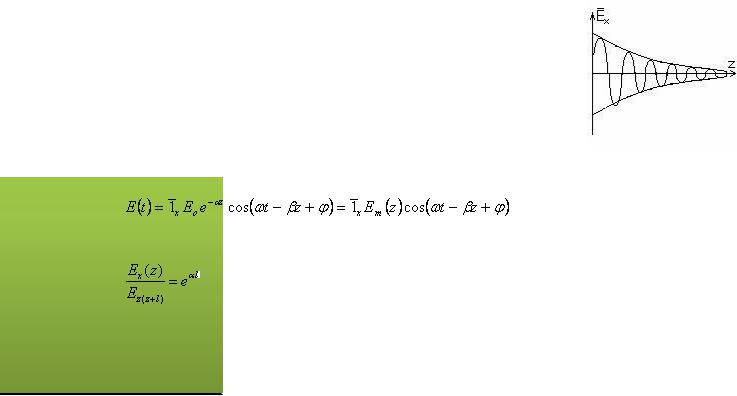
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Для описания любых процессов радиотехники достаточно классической электродинамики. Как известно источниками электромагнитного поля являются электрические заряды. Неподвижные электрические заряды создают только электрическое поле. Движущиеся заряды — создают как электрическое, так и магнитное поле. Разделение электромагнитного поля на электрическое и магнитное носит относительный характер, и зависит от выбора системы координат. Прямолинейно движущийся электрический заряд создает электрическое и магнитное поле, но для прямолинейно движущегося наблюдателя он создает только электрическое поле. Источником электромагнитного поля являются не только отдельные заряды, но и электрические и конвекционные токи (токи - это упорядоченно движущиеся электрические заряды).
ПЛОСКИЕ ВОЛНЫ В ОДНОРОДНОЙ ИЗОТРОПНОЙ СРЕДЕ С ПРОВОДИМОСТЬЮ ОТЛИЧНОЙ ОТ НУЛЯ.
В среде с проводимостью отличной от нуля энергия электромагнитной волны частично расходуется на возбуждение и поддержание токов проводимости, т.е. волна в процессе распространения затухает. В общем случае наряду с джоулевыми потерями в среде могут присутствовать также диэлектрические и магнитные потери. В этом случае:
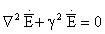 (1)
(1)
 (2)
(2)
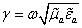 (3)
(3)
В этом случае решения по форме совпадают с решениями, полученными в предыдущем параграфе.
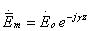 (4)
(4)
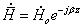 (5)
(5)
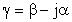 (6)
(6)
Перейдем для уяснения физического смысла к мгновенным значениям:
Степень убывания амплитуды:
67 |
-характеризует ослабление волны. |
|

В некоторый фиксированный момент времени изобразим 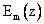 : Отметим физический смысл: — комплексная постоянная распределения.
: Отметим физический смысл: — комплексная постоянная распределения.
— ее действительная часть, смысл тот же, что и у k, т.е. показывает изменение фазы волны в радианах при прохождении волной пути в 1 метр (фазовая постоянная); — мнимая часть . Показывает восколько раз уменьшается амплитуда волны на пути в 1 метр (постоянная затухания).
Уменьшение амплитуды волны в процессе распространения характеризуют величиной затухания:
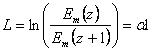 ,[Нп] (7)
,[Нп] (7)
 ,[дБ]
,[дБ]
Будем рассматривать случай, когда потери в среде вызваны конечной проводимостью (только Джоулевы потери):
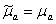 и
и  ,
, 
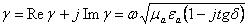 (8)
(8)
Хотим получить выражения для и . Возведем в квадрат и выделим реальные и мнимые величины. Получим:
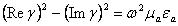 ( )
( )
Выразим из второго уравнения мнимую часть и подставим в первое.
Решаем квадратное уравнение:
Так как слева стоит квадрат, то в этом соотношении учитывается только знак "+". Тогда: 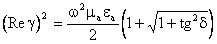
Откуда получаем:  (9)
(9)
Воспользуемся соотношением ( ) из которого следует, что мнимая 68 часть: 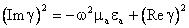 .
.

Подставим (9) в ( ):
Так как слева стоит квадрат, то правая часть не может быть отрицательной. Получаем:
(10)
Проанализируем экспоненциальный множитель  . Подстановка
. Подстановка
вместо 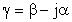 . Можно получить:
. Можно получить: 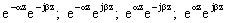 . Физически реальными являются первое и последнее произведения. Первое из них соответствует затухающей волне, распространяющейся в положительном направлении оси z, а последнее — в отрицательном направлении оси z. Таким образом поле плоской волны, распространяющейся в среде с потерями, может быть представлено следующими соотношениями:
. Физически реальными являются первое и последнее произведения. Первое из них соответствует затухающей волне, распространяющейся в положительном направлении оси z, а последнее — в отрицательном направлении оси z. Таким образом поле плоской волны, распространяющейся в среде с потерями, может быть представлено следующими соотношениями:
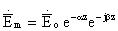 (11)
(11)
 (12)
(12)
В данном случае характеристическое сопротивление среды является комплексной величиной.
Целесообразно поступить следующим образом:
(13)
69 
