
EMPiV
.pdf
Эту пропорциональность между амплитудами можно описать матричным соотношением (рис. 4.3):
матрицы-столбцы из соответствующих амплитудЕи Н связаны матрицейпередачи
(4.10)
Матрица передачи для слоя вещества при прохождении электромагнитных волн полностью совпадает с матрицей передачи отрезка длинной линии для волн напряжения и тока. Различие в знаках связано с противоположными направлениями отсчета продольной координаты: в длинной линии направление х > 0 выбрано от нагрузки к источнику. Оно исчезает в (4.10), если координату z2 взять меньшей, чем z1, то есть при отрицательных значениях z. Еще одна аналогия наблюдается для трансформации сопротивления. Если ввести понятие комплексного сопротивления для данной точки z как отношения амплитуд электрического и магнитного полей E(z) /H(z) ≡Z(z) , то, разделив первое выражение (4.9) на второе, после простых тождественных преобразований получим:
. |
(4.11) |
Отношение комплексных амплитудЕи Н изменяется(трансформируется) в пространстве по такому же закону, что иотношение V и Iвдоль длинной линии (3.58) с учетомнаправления отсчета. Используя эту аналогию, при наличиистоячих электромагнитных волн можно проводить расчеты, подобные анализу свойств длинных линий на основе теории цепейс распределенными параметрами.
80

32. ПАДЕНИЕ ПЛОСКОЙ ВОЛНЫ НА ПОВЕРХНОСТЬ ИДЕАЛЬНОГО МЕТАЛЛА
Плоские однородные волны в хорошо проводящих средах
В хорошо проводящих средах (например, в металлах) tgδ>> 1, относительная магнитная проницаемость μ = 1 (μа= μ0). При tgδ>> 1 в общих выражениях коэффициента фазы (4.46) и коэффициента затухания (4.47) можно пренебречь единицей по сравнению с tgδ. В результате получаем
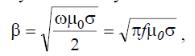 (4.69)
(4.69)
(4.70)
Постоянные β и α нелинейно зависят от частоты, следовательно, свойства волны на разных частотах будут существенно различаться. Формулы для фазовой скорости, длины волны и характеристического сопротивления в таких средах принимают вид
Сравним параметры плоских волн, распространяющихся в вакууме и меди (См/м) на частоте 1 МГц: 710 =ζ5,65
Коэффициент затухания волны, распространяющейся в меди при частоте 1 МГц равен α = 14935 1/м. Глубина проникновения волны в медь на частоте 1 МГц составляет 67 мкм. Приведенные примеры показывают, что электромагнитная волна на частотах радиодиапазона практически не проникает вглубь
81 проводника.

33. ПРИНЦИП ДЕЙСТВИЯ ДИЭЛЕКТРИЧЕСКОГО И МЕТАЛЛИЧЕСКОГО ВОЛНОВОДОВ.
Диэлектрический волновод — волновод, состоящий только из диэлектрических материалов, или образованный диэлектрическими материалами.
Рабочий диапазон диэлектрических волноводов: 10^9 ... 10^16 Гц.
Цилиндрические в сечении диэлектрические волноводы для волн оптического диапазона называются оптическими волокнами.
Часто имеют диэлектрическую проницаемость, изменяющуюся в зависимости от расстояния до оси волновода. Передача электромагнитной волны в таких волноводах происходит за счет полного внутреннего отражения.
Затухание в диэлектрических волноводах вызывается омическими потерями (растут с увеличением частоты) и рассеянием на неоднородностях и изгибах
Металлический волновод — волновод, изготавливаемый из латуни, алюминия и покрытый изнутри серебром или другим хорошо проводящим металлом.
Волноводы в сечении могут быть круглыми, прямоугольными, эллиптическими. Возможно проводить изгибы волноводов.
Сечение волноводов зависит от используемого диапазона частот. К примеру сечение 16×8 мм для Ku-диапазона. Волноводы с 2-х сторон имеют фланцы для их крепления к другим элементам волноводной техники.
Фланцы имеют отверстия для винтов. Фланцы могут быть круглыми или прямоугольными.
Волноводы используют в СВЧ диапазоне частот. В более низком диапазоне частот используют кабели, что связано с непомерно большим сечением волноводов в ВЧ диапазоне частот.
При соединении отрезков волноводов друг с другом для уменьшения потерь СВЧ энергии используют металлические прокладки, во фланцах делают резонансные четвертьволновые канавки.
Качество передачи энергии волноводом характеризуется следующими параметрами: Кз — затухание энергии, КСВ (коэффициент стоячей волны) или КБВ (коэффициент бегущей волны).
Волноводы могут быть переменного сечения — для передачи определенных волн и затухания других.
Металлические волноводы широко используют в космической технике.
82

34. ПАДЕНИЕ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ ПОГЛОЩАЮЩЕЙ СРЕДЫ
Пусть плоская волна падает под углом θ на плоскую границу раздела двух сред, из которых первая - идеальный диэлектрик, а вторая обладает проводимостью. Общие формулы, определяющие поля падающей, отраженной и преломленной волн, можно использовать и в этом случае, если считать в них параметры k2и Zc2 комплексными величинами. Из второго закона Снеллиуса (7.11) следует, что при этом sin 8 становится комплексным, так как k1и sin θ - действительные числа, а k2 = k2комплексная величина.
Это означает, что параметр θ нельзя рассматривать как геометрический угол, под которым распространяется преломленная волна. Введем обозначения
и х = const соответственно. Следовательно, волна (7.46) является неоднородной плоской волной. Направление распространения этой волны образует некоторый уголθД с осью X, который называют истинным (или действительным) углом преломления (рис.7.7). Поверхности равных фаз представляют собой параллельные плоскости, нормаль к которым образует с осями X и Z углы θд и π/2-θд соответственно. Уравнение,
83

определяющее такие плоскости, может быть также записано в виде х cosθД + zsinθД = const. Сравнивая это равенство с уравнением (7.47), находим, что
Отметим, что в рассматриваемом случае ПРФ повернуты относительно ПРА на уголθД (см. рис.7.7).
Амплитуды векторов Е и Н экспоненциально убывают в направлении нормали к поверхности раздела (вдоль оси X). Имеется продольная по отношению к направлению распространения преломленной волны составляющая вектора Н (в случае нормальной поляризации) или продольная составляющая вектора Е (в случае параллельной поляризации).
Поле в первой среде складывается из падающей и отраженной волн и не имеет принципиальных отличий от поля, возникающего при отражении волны от границы раздела двух диэлектриков.
Аналогичные результаты можно получить, анализируя случай параллельной поляризации.Практически важным является случай, когда вторая среда оптически намного плотнее первой:
Это означает, что при любом угле падения ср на поверхность хорошо проводящей среды преломленная волна распространяется практически вдоль нормали к поверхности раздела. Поверхности равных фаз и поверхности равных амплитуд при этом практически совпадают, и волну можно считать однородной. Продольная по отношению к направлению распространения составляющая вектора Н (или, в случае параллельной поляризации, вектора Ё)будет пренебрежимо мала по сравнению с поперечной составляющей. Можно считать, таким образом, что волна является поперечной, причем векторы Е и Н, в ней
сдвинуты по фазе друг относительно друга на угол  Иными словами, при анализе плоской волны, возникающей в результате пре-
Иными словами, при анализе плоской волны, возникающей в результате пре-
ломления на поверхности хорошо проводящей среды, можно использовать все основные соотношения, полученные в 6.1.4 при исследовании свойств плоской волны, свободно распространяющейся в хорошо проводящей безграничной однородной изотропной среде.
Подчеркнем, что амплитуды векторов Е и Н преломленной волны в металле быстро убывают с удалением от границы раздела и волна фактически существует лишь в тонком слое вблизи поверхности раздела.
84 

35. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ ЛЕОНТОВИЧА-ЩУКИНА
Задача определения поля в присутствии металлических тел с конечной проводимостью имеет большое значение. Ее решение часто можно упростить введением приближенных граничных условий Леонтовича-Щукина. В отличие от обычных граничных условий, связывающих значения составляющих поля на границе раздела в разных средах, граничные условия Леонтовича-Щукина
выражают связь между составляющими векторов Ё и Н в одной среде.
В (7.6) было показано, что при выполнении условия (7.49) плоская волна, падающая под любым углом ср на границу раздела двух сред, возбуждает во второй среде плоскую волну, распространяющуюся практически вдоль нормали к поверхности раздела. Так как ПРФ и ПРА такой волны практически совпадают, то ее можно считать однородной. При этом должны выполняться соотношения
где п0-единичная нормаль, внешняя к плотной среде.
85

Соотношение (7.52) называют приближенным граничным условием Леонтовича-Щукина. Из него следует, что на поверхности реального проводника касательная составляющая напряженности электрического поля отлична от нуля. Отметим, что граничное условие Леонтовича-Щукина в предельном случае ζ2→∞совпадает с обычным условием Е1η=0, которое должно выполняться на поверхности идеального проводника.
Так как характеристическое сопротивление в случае хорошо проводящей среды мало, то и касательная составляющая вектора Е на поверхности такой среды будет мала. Однако она определяет нормальную к поверхности проводника компоненту вектора Пойнтинга, т.е. уходящий в металл поток энергии. В инженерных расчетах касательную составляющую вектора Е на поверхности реального проводника обычно не учитывают, кроме тех случаев, когда требуется определить потери в проводнике, т.е. считают, что структура поля над реальным проводником такая же, как и над идеальным проводником той же конфигурации.
Граничное условие (7.52) является приближенным. Это следует непосредственно из его вывода, при котором предполагалось, что образующиеся во второй среде волны распространяются строго по нормали к поверхности раздела. В действительности направление распространения образует некоторый (в случае металлов очень малый) угол с нормалью к поверхности раздела.
Условие (7.52) было получено в предположении, что граница раздела является плоской. При произвольной форме поверхности раздела условием (7.52) можно пользоваться только в тех случаях, если минимальный радиус кривизны поверхности Rminзначительно превышает глубину проникновения 0 (см. 6.1.6):
86

36. ПОТЕРИ ЭНЕРГИИ В ПРОВОДНИКЕ. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ МОЩНОСТИ ДЖОУЛЕВСКИХ ПОТЕРЬ В ПРОВОДНИКАХ.
Пусть металлический объект, размеры и минимальный радиус кривизны поверхности которого велики по сравнению с глубиной проникновения, находится в монохроматическом электромагнитном поле. Под воздействием этого поля в металле наводятся электрические токи, на поддержание которых расходуется электромагнитная энергия. Вычислим соответствующую этому процессу среднюю за период мощность джоулевых потерь. Запишем уравнение баланса средних за период значений мощности для объема V, занимаемого рассматриваемым объектом. Учитывая, что внутри объема Vнет сторонних источников, приходим к равенству 0 = РПср+PΣcp, из которого следует, что
где n0-орт внешней нормали к поверхности рассматриваемого объекта S. Как видно, для определения мощности Рпсрнет необходимости вычислять поле внутри объекта, достаточно проинтегрировать по S перпендикулярную к ней составляющую комплексного вектора Пойнтинга. Знак минус в формуле (7.54) объясняется тем, что джоулевы потери определяются потоком энергии, направленным внутрь проводника, а орт п0 направлен из объема Vв окружающее пространство. Нормальная составляющая вектора Пойнтинга определяется касательными составляющими векторов
Где μ2 и ζ2 - абсолютная магнитная проницаемость и удельная проводимость проводника.
Таким образом, средняя за период мощность джоулевых потерь в проводнике
Как уже отмечалось, структура поля у поверхности реального проводника близка к структуре поля у такой же поверхности идеального проводника. Поэтому при вычислении потерь обычно
87

предполагают, что 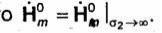 Это предположение существенно
Это предположение существенно
упрощает расчеты, обеспечивая достаточную для инженерной практики точность результатов.
88

37. МЕТОДЫ СНИЖЕНИЯ ТЕПЛОВЫХ ПОТЕРЬ В ПРОВОДНИКАХ.
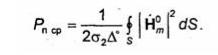 (1)
(1)
Средняя за период мощность джоулевых потерь в проводнике, находящемся в электромагнитном поле.распростаняющейся волны определяется по формуле(1) , где S – поверхность проводника, взаимодействующая в волной. Для уменьшения таких потерь необходимо;
1) уменьшать активную часть поверхностного сопротивления проводника (2), для этого следует токонесущие поверхности выполнять их металлов с большой проводимостью ζ ;
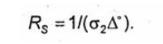 (2)
(2)
на практике обычно на частотах менее 2 ГГц применяют алюминий.на более высоких частотах используют медь и сплавы меди
2)токонесущие поверхности проводников покрывают специальными защитными покрытиями , специальными лаками, а в некоторых наиболее ответственных случаях используют тонкую пленку серебра; подобные защитные покрытия предотвращают появление окисных пленок на поверхности металла, например меди; следует отметить, что поверхностное сопротивление окисной пленки меди на порядок выше поверхностного сопротивления меди
3)для уменьшения поверхности S, токонесущие поверхности проводников шлифуют и полируют , уменьшая высоту неровностей поверхности проводника.
89
