EMPiV
.pdf
9. КЛАССИФИКАЦИЯ СРЕД
Свойства среды по отношению к электромагнитному полю определяются параметрами ε, μ и ζ. Различают следующие среды:
линейные,в которых параметры ε, μ и ζ не зависят от величины электрического и магнитного полей, и
нелинейные, в которых параметры ε, μ и ζ (или хотя бы один из них) зависят от величины электрического или магнитного поля .
Все реальные среды, по существу, являются нелинейными с Однако при не очень сильных полях во многих случаях можно -пренебречь зависимостью параметров ε, μ,ζ от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна. В дальнейшем будут рассматриваться только линейные среды.
В свою очередь, линейные среды делятся наоднородные и неоднородные, изотропные и анизотропные.
Однородныминазывают среды, параметры ε, μ и ζ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках.
Среды, у которых хотя бы один из параметров ε, μ илиζ является функцией координат, называют неоднородными.
Если свойства среды одинаковы по разным направлениям, то среду называют изотропной.
Соответственно среды, свойство которых различны по разным направлениям, называют анизотропными. В изотропных средах векторы Р иЕ, D и Е, а также М и Н, В и Н параллельны, а в анизотропных средах они могут быть не параллельными. В изотропных средах ε, μ и ζ -скалярные величины.
В анизотропных по крайней мере один из этих параметров ' является тензором.
20
10. НЕПРИМЕНИМОСТЬ УРАВНЕНИЙ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
Уравнениями Максвелла в дифференциальной форме удобно пользоваться при анализе электромагнитных полей в средах, параметры ε, μ и ζ а которых - непрерывные функции координат (или не зависят от координат). На практике, однако, рассматриваемая область может состоять из двух (и более) разнородных сред. При анализе макроскопических свойств поля обычно считают, что параметры ε, μ и ζ (или по крайней мере один из них) на границе раздела сред меняются скачком. При этом пользоваться уравнениями Максвелла в дифференциальной форме на границе раздела неудобно, и для изучения поведения векторов поля при переходе из одной среды в другую следует исходить из уравнений Максвелла в интегральной форме (1).
(1)
21
11. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ НОРМАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЕЙ
Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными условиями. Граничные условия для нормальных составляющих векторов
электрического и магнитного полей могут быть получены из третьего (1.43) и четвертого (1.46) уравнений Максвелла в интегральной форме. Сравнивая эти уравнения, равенство (1.46) может быть формально получено из уравнения (1.43), если в последнем заменить D на В и положить ρ = 0. Вывод граничного условия для нормальной составляющей вектора D, а из него указанными преобразованиями получим граничное условие для нормальной составляющей вектора В.
На поверхности раздела So двух изотропных сред, характеризуемых
параметрами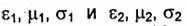 
, в. окрестности произвольно выбранной точки М выделим достаточно
малый элемент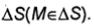 
. Элемент
S должен быть достаточно мал, чтобы, его можно было считать плоским, и чтобы в обеих средах распределение нормальной компоненты вектора D можно было считать равномерным в пределах S.
Построим на элементе ΔS прямой цилиндр
высотой 2Δ/h так, чтобы его основания находились в разных средах (рис.1.14), и применим к нему третье уравнение Максвелла в интегральной форме (1.43):
22
Если заряд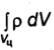 
не сосредоточен на поверхности раздела, т.е. не является поверхностным, то при любой конечной величине объемной
плотности заряда р правая часть формулы (1.82) равна нулю, а нормальная компонента вектора D непрерывна при переходе из одной среды в другую:
Когда заряды распределены вдоль поверхности раздела в виде бесконечно тонкого слоя. Такие заряды называют поверхностными и характеризуют плотностью поверхностных зарядов ps (поверхностной плотностью зарядов),
определяемой 
где ∆Q - заряд на элементе поверхности ∆S. Как видно из (1.84), ρs (Кл/м2). Пусть теперь на границе раздела имеются поверхностные заряды с
плотностью ρs. В этом случае правая часть уравнения (1.82) уже не будет равна нулю. Считая распределение заряда на площадке ΔS равномерным (в противном случае нельзя считать равномерным распределение D1n и D2n), разделим обе части уравнения (1.82) на ΔS. В результате получим
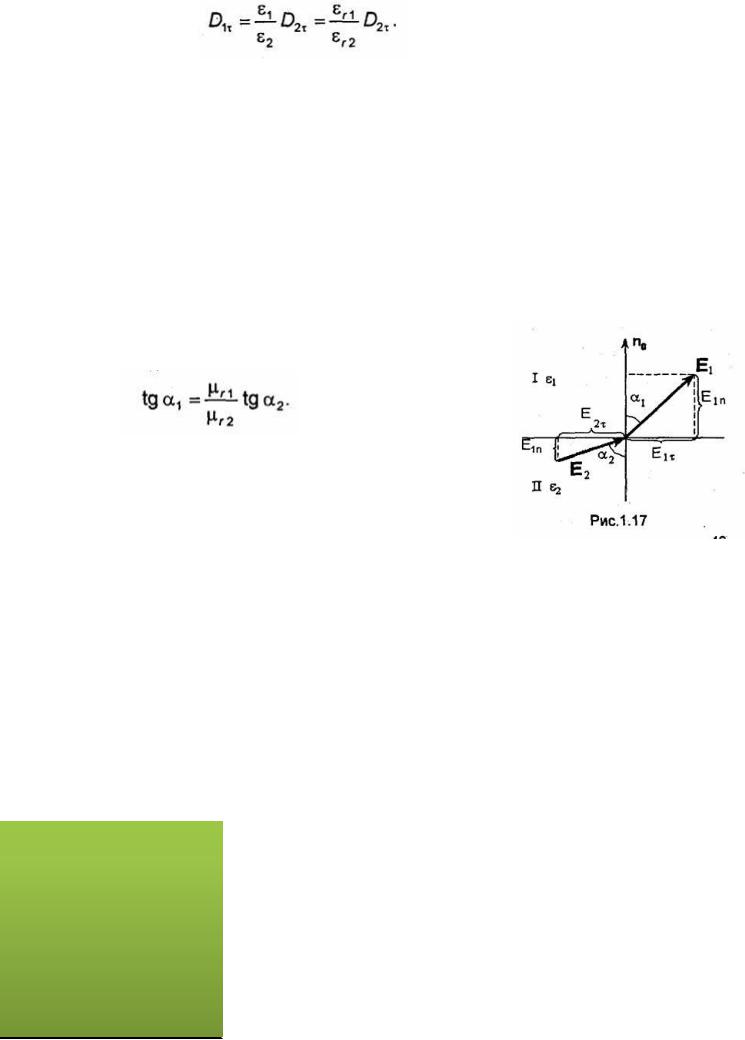
D1n-D2n=ρs. (1.85)
Соотношение (1.85) показывает, что при переходе из одной среды в другую нормальная компонента вектора D претерпевает разрыв (скачок), равный плотности поверхностных зарядов, распределенных по границе раздела.
Выражая в этом соотношении D1n и D2n через Е1n и Е2п с помощью равенства D = εE, получаем граничное условие для нормальных компонент
вектора Е: 
23 Если на границе раздела отсутствуют поверхностные заряды, то условие (1.86)
можно представить в виде
Соотношение (1.87) показывает, что нормальная составляющая вектора Е при переходе через незаряженную поверхность раздела двух сред имеет разрыв, величина которого определяется отношением диэлектрических проницаемостей этих сред. Наличие плотности поверхностных зарядов ρs в рассматриваемой точке приводит к изменению величины разрыва, увеличивая или уменьшая его. При определенном значении ρs нормальная составляющая вектора Е может даже оказаться непрерывной.
В каждой точке внутри реального заряженного слоя
составляющая Dn непрерывна. При замене реального слоя зарядов бесконечно тонким (т.е. поверхностными зарядами) приходится считать, что Dn изменяется скачком.
Граничное условие для нормальной составляющей вектора В, может быть получено из (1.85), если положить ρs=0 и заменить D1n и D2n на В1л и В2n. При
этом придем к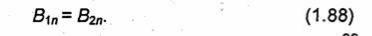 
Из (1.88) следует, что составляющая Вn непрерывна при переходе через границу раздела двух сред. Нормальная составляющая вектора Н имеет разрыв, величина которого определяется отношением магнитных проницаемостей. Выражая в равенстве (1.88) B1n и В2n через H1п и Н2п, получаем
12. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ КАСАТЕЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЕЙ
Граничные условия для касательных составляющих векторов электрического и магнитного полей могут быть получены из второго (1.37) и первого (1.31) уравнений Максвелла в интегральной форме. В рассматриваемом случае можно считать, что контур Г в уравнении (1.37) не зависит от времени. Поэтому, внося производную по t под знак интеграла, получаем
Сравнивая (1.90) с первым уравнением Максвелла (1.31), равенство (1.90) может быть получено . из уравнения (1.31), если в последнем положить j = 0 и заменить Н на Е и D на В. Следовательно, можно ограничиться выводом граничного условия для касательной составляющей вектора Н из (1.31), а затем с помощью указанных преобразований получить граничное условие для касательной составляющей вектора Е.
Пусть So - граница раздела двух изотропных сред, характеризуемых
|
параметрами |
. Из произвольной точки MЄS проведем |
|
единичную нормаль n0, направленную из второй среды в первую (рис. 1.15). |
|
|
Через n0 проведем плоскость Р. На линии пересечения поверхности раздела So с |
|
|
плоскостью Р выделим достаточно малый отрезок l содержащий |
|
24 |
точку М. Размеры отрезка должны быть такими, чтобы, его можно было считать |
|
прямолинейным и чтобы распределение касательной составляющей вектора Н в |
||
пределах l в обеих средах можно было считать равномерным. В плоскости Р построим прямоугольный контур ABCD,
Стороны АВ и CD параллельны l и находятся в разных средах. В
точке М проведем единичную касательную η0 к линии пересечения поверхности раздела S с плоскостью Р и единичную нормаль No к плоскости Р так, чтобы
орты п0, η0 и No составляли правую тройку векторов: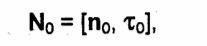 
а обход контура ABCD образовывал правовинтовую систему с вектором No- Применим к контуру ABCD первое уравнение Максвелла (1.31):
где ΔS - площадь, охватываемая контуром ABCD, a dS = NodS. Левую часть этого равенства можно представить в виде суммы четырех интегралов:
ВС и DA параллельны и равны 2Δh, а направление dl определяется выбранным
обходом контура: 
Устремляя h к нулю (при этом стороны АВ и CD совпадут с l) и учитывая, что функции Н и dDldt являются ограниченными, приходим к
где Н1 и Н2 - значения вектора Н на границе раздела S в первой и второй средах соответственно, а Н1η и H2η- проекции векторов Н1 и Н2 на касательную η0. Используя эти соотношения при переходе к пределу при Δh→0 в уравнении
(1.92), получаем 
Если на границе раздела отсутствуют поверхностные токи, правая часть
равенства (1.93) равна нулю. В этом случае касательная составляющая вектора Н оказывается непрерывной:
25
Касательная составляющая вектора В, претерпевает разрыв, определяется отношением магнитных проницаемостей:
Когда токи распределены вдоль поверхности раздела в виде бесконечно тонкого
слояповерхностные токи 
(А/м).
где i0- единичный вектор, указывающий направление движения положительных зарядов в данной точке; ΔL-элемент линии, перпендикулярный вектору i0; /-ток, протекающий через ΔL (рис.1.16). В этом случае правая часть равенства (1.95) уже не будет равна нулю. Считая распределение поверхностного тока на отрезке ΔL равномерным (если это не выполняется, нельзя считать равномерным распределение касательной составляющей вектора Н), преобразуем правую часть указанного равенства следующим образом:
где jSN - проекция вектора js на направление No. Подставляя это выражение в (1.93) и деля обе части получающегося равенства на l, приходим к соотношению
Уравнение (1.97) справедливо для любого направления касательной ηo, и его можно переписать в векторной форме
где Н1 и Н2 - значения вектора Н у границы раздела в первой и во второй средах соответственно.
Уравнения (1.97) и (1.98) показывают, что при переходе через границу раздела, по которой текут поверхностные токи, касательная составляющая вектора Н претерпевает разрыв, величина которого определяется значением плотности поверхностных токов в рассматриваемой точке. Переходя в уравнении (1.97) к касательным составляющим вектора В, получаем
Отметим, что поверхностные токи, как и поверхностные заряды, обычно вводят для упрощения расчетов вместо реального тонкого слоя токов, когда не интересуются распределением поля внутри слоя. В каждой точке внутри реального токового слоя касательная составляющая вектора Н непрерывна, но ее значения по разные стороны слоя отличаются на конечную величину. Поэтому при замене реального токового слоя бесконечно тонким (т.е. поверхностными токами) приходится считать, что Hη изменяется скачком.
|
Граничное условие для касательной составляющей вектора Е из равенства |
|
(1.97) на основе i указанных выше изменений. Полагая в (1.97)jSN = О и заменяя |
|
касательные составляющие вектора Н на соответствующие касательные |
|
составляющие вектора Е, приходим к: |
26 |
Равенство (1.99) показывает, что касательная составляющая |
вектора Е непрерывна при переходе через границу раздела двух сред. |
Касательная составляющая вектора D, наоборот, претерпевает разрыв, величина которого зависит от соотношения между диэлектрическими проницаемостями. Выражая E1η и Е2η в равенстве (1.99) через D1η и D2η,
получаем Граничные условия, полученные для составляющих векторов электрического
поля, показывают, что на границе раздела векторы Е и D преломляются. Обозначим углы между нормалью п0 к поверхности раздела и векторами Е1 и Е2 соответственно через си и α2 (рис. 1.17). Так
как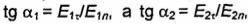 
то, используя граничные условия (1.86) и (1.99), получаем, что при отсутствии поверхностных зарядов на границе раздела
справедлив: 
В изотропных средах векторы Е и D направлены одинаково. Поэтому соотношение (1.100) определяет также преломление вектора D. Очевидно,
аналогичное соотношение может быть получено и для векторов магнитного поля. Пусть α1 и α2- углы между нормалью п0 и векторами H1 и Н2. Тогда, как следует из уравнений (1.89) и (1.94), имеет место соотношение
В случае изотропных сред это равенство определяет также изменение ориентации вектора В.
27
13. ГРАНИЧНЫЕ УСЛОВИЯ НА ПОВЕРХНОСТИ ИДЕАЛЬНОГО ПРОВОДНИКА
На поверхности раздела любых двух изотропных сред должны
выполнятьсяграничные условия: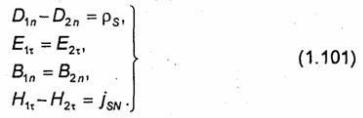 
Они справедливы для любых электромагнитных процессов, рассматриваемых в макроскопической электродинамике. Не включенные в систему (1.101) граничные условия для составляющих Dη, Еп, Вη и Нп являются следствиями соотношений (1.101) и уравнений состояния (1.53). Граничные условия (1.101) в
векторной форме: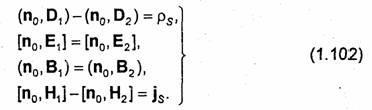 
При изучении переменных электромагнитных полей вблизи поверхности металлических тел часто предполагают, что рассматриваемое тело является идеально проводящим. При этом граничные условия упрощаются, так как в среде с ζ = ∞ поле отсутствует. Действительно, плотность тока
проводимости j должна быть ограниченной величиной. Поэтому из закона Ома в дифференциальной форме (1.9) следует, что напряженность электрического поля внутри идеального проводника должна быть равна нулю. Полагая во втором уравнении Максвелла Е = 0, получаем dB/dt= 0. Так как поле считается переменным, то последнее равенство выполняется только при В = 0.
Пусть идеально проводящей является вторая среда. Тогда D2= E2= В2= Н2= 0 и условия (1.101) принимают вид
Физическая сущность граничных условий Граничные условия для составляющих вектора Е. Пусть имеются две
изотропные среды с общей границей раздела, характеризуемые диэлектрическими проницаемостями ε 1и ε 2. Предположим, что на границе раздела сред отсутствуют свободные поверхностные заряды (ps = 0). Под воздействием внешнего электрического поля обе среды поляризуются, причем вектор Р, характеризующий поляризацию, будет иметь разные значения в этих
средах, так как 
- Если вектор Е, и вектор Р перпендикулярны поверхности раздела (рис.1.18), то на ней появятся некомпенсированные
28 поверхностные заряды, связанные с молекулами вещества. На рис.1.18 когда ε2> ε1. И соответственно вторая среда поляризуется легче, чем первая. Во
второй среде больше молекулярных диполей, ориентированных параллельно вектору Е. Образующиеся на границе раздела нескомпенсированные поверхностные заряды в примере являются положительными (рис.1.18,6). Если векторы Е и Р параллельны поверхности раздела, то такие заряды не возникают (рис. 1.19). При произвольной ориентации вектора Е(или Р) у границы раздела величина появляющихся на ней нескомпенсированных поверхностных зарядов определяется изменением значений нормальной составляющей вектора Р при переходе через границу раздела.
Выберем на поверхности раздела сред некоторую точку М и рассмотрим поведение составляющих вектора Е при переходе через границу раздела. Электрическое поле в рассматриваемой точке складывается из первичного поля, вызвавшего поляризацию сред, и вторичного поля, создаваемого поляризационными зарядами. Все заряды, кроме расположенных в непосредственной близости к рассматриваемой точке, создают в этой точке в соответствии с законом Кулона непрерывное поле. Исключение составляет поле, создаваемое некомпенсированными "связанными" поверхностными зарядами, расположенными в непосредственной близости к точке М. Эти заряды создают в точке М дополнительное электрическое поле Е, нормальные к границе раздела составляющие которого по разные стороны от этой границы (ΔЕ1п и Е2п) равны по величине и противоположны по направлению (рис. 1.20), а касательные - равны по величине и направлению (аналогично полю точечного заряда, расположенного в точке М). Это означает, что касательная составляющая напряженности дополнительного электрического поля Е непрерывна, а нормальная имеет разрыв. Складывая дополнительное поле с первичным полем и полем всех остальных поляризационных зарядов, получаем, что у полного поля в точке М нормальная составляющая вектора Е имеет разрыв
(Е1n≠Е2п), а касательная - непрерывна (Е1η= Е2η).
Наличие на границе раздела в точке М плотности свободных поверхностных зарядов (ps≠0) не может нарушить непрерывность касательной составляющей вектора Е, но приводит к изменению величины разрыва его нормальной составляющей.
Граничные условия для составляющих вектора В. Пусть имеются две изотропные среды с общей границей раздела, характеризуемые магнитными проницаемостями μ 1 и μ2. Предположим вначале, что на границе раздела отсутствуют поверхностные токи, обусловленные движением свободных зарядов (js= 0). Под воздействием внешнего магнитного поля обе среды намагничиваются. На рис. 1.21 система кольцевых электрических токов, эквивалентных ориентированным по полю магнитным моментам молекул, которую в
средах I и II можно заменить противоположно направленными поверхностными токами (РИС. 1.21, б) c плотностями 
.
29