EMPiV
.pdf
Рассмотрим, как меняется фаза и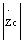 
при изменении = 0... .
С ростом проводимости характеристическое сопротивление по модулю убывает.
Вывод: По определению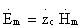 
. В среде с проводимостью отличной
от нуля при постоянной напряженности электрического поля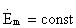 
с ростом проводимости увеличивается амплитуда магнитной
компоненты 
.
Физически это можно объяснить:
в среде с проводимостью равной нулю присутствуют только токи
смещения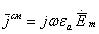 
. Если проводимость равна нулю, то в среде появляются проводящие токи. Причем при неизменной напряженности электрического поля и диэлектрической проницаемости среды плотность тока остается неизменной.
Проанализируем полученный результат. Пусть 
имеет только иксовую
составляющую, тогда вектор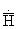 
будет иметь одну составляющую, ориентированную по оси y, если волна распространяется вдоль оси z.
Будем предполагать, что амплитуда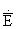 
является действительной величиной.
Перейдем к мгновенным значениям: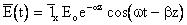 
Проанализируем. Поверхность равных фаз определяется уравнением z =const. Поверхность равных амплитуд совпадает с поверхностью равных фаз, т.е. рассмотренный процесс является плоской однородной волной.
Имеются составляющие поля, взаимно ортогональные и перпендикулярные направлению распространения волны, т.е. она является и поперечной. Амплитуда волны экспоненциально убывает в процессе ее распространения. В данном случае магнитная
составляющая поля отстает от электрической на угол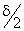 
. Проанализируем основные характеристики электромагнитной волны. Фазовая скорость равна:
70
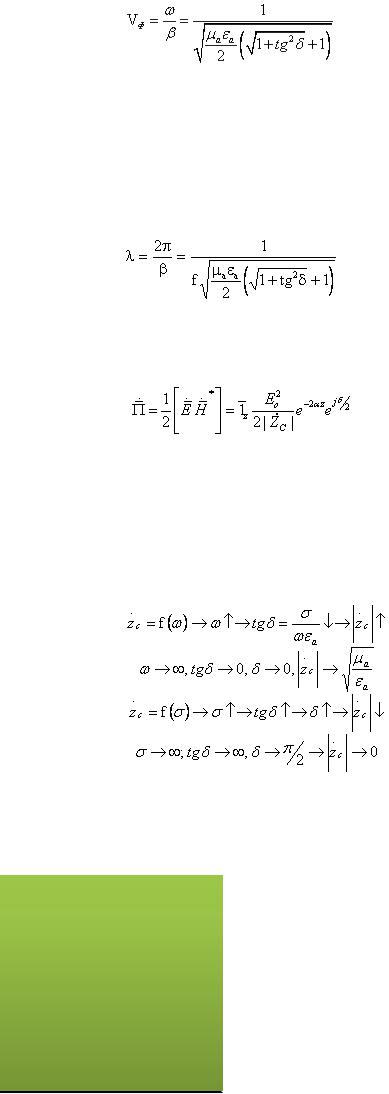
Из этого уравнения следует, что так как >k, то фазовая скорость в среде с потерями меньше фазовой скорости в среде без потерь, так
как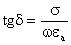 
.
В данном случае фазовая скорость является функцией частоты. С ростом частоты tg убывает и фазовая скорость возрастает. Фазовая скорость зависит от проводимости среды. С ростом проводимости tg увеличивается и фазовая скорость убывает.
Из соотношения видно, что в среде с потерями меньше в среде без потерь. С ростом проводимости tg увеличивается и убывает. Распространение волны сопровождается переносом энергии. Вектор Пойнтинга:
Среднее за период значение: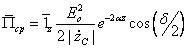 
Если мы попытаемся вычислить скорость распространения энергии, то
все данные есть: 
После подстановки получим, что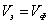 
.
По рассмотренным результатам можно отметить, что характеристики плоских волн в среде с потерями и без потерь существенно отличаются. Главное принципиальное отличие состоит в том, что Vф , VЭ , zс в среде без потерь неизменны при любых частотах и определяются только электродинамическими параметрами среды. В среде с потерями эти же параметры являются функциями частоты. Явление зависимости параметров электромагнитной волны от частоты называется дисперсией, а соответствующие среды называются диспергирующими. Дисперсия возможна и в средах без потерь, если хотя бы один из электродинамических параметров является функцией
71 частоты.
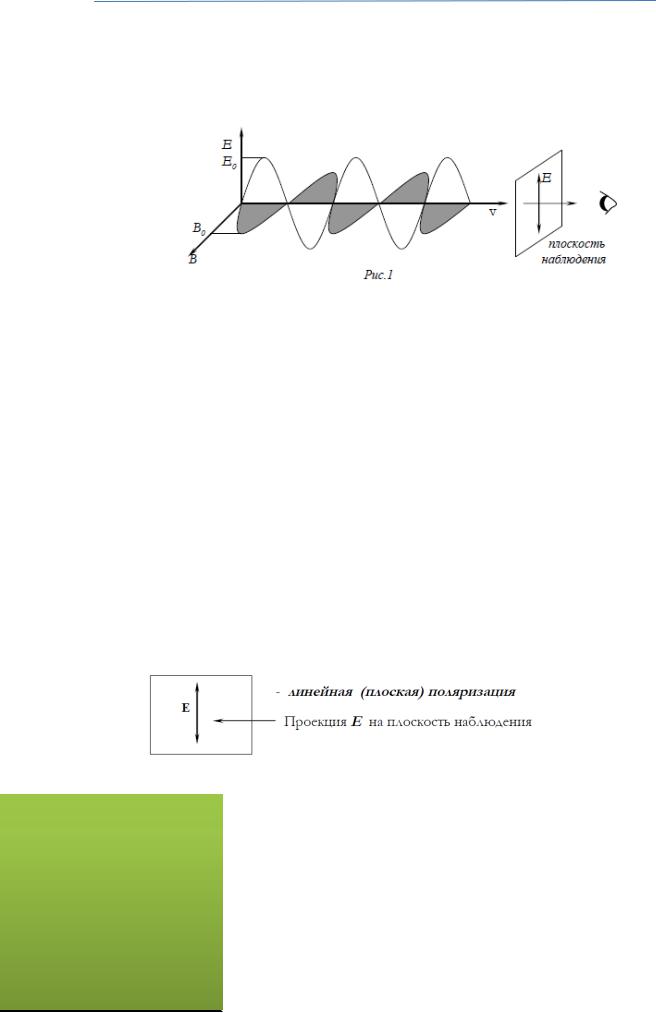
27. ПОЛЯРИЗАЦИЯ ВЕКТОРОВ ПОЛЯ. ВИДЫ ПОЛЯРИЗАЦИИ.
В любой электромагнитной волне векторы напряженности электрического поляЕ, индукции магнитного поля В и вектор скорости волны v образуют взаимно перпендикулярную тройку векторов: Е ┴ В ┴ v . Элементарная структура электромагнитной волны представлена на Рис.1
Поскольку при распространении волны вектораВи Е всегда взаимно перпендикулярны, то они изменяются в пространстве одинаковым образом, описывая одинаковые по форме кривые, но во взаимно перпендикулярных плоскостях. Поэтому достаточно знать, как изменяется в пространстве один из этих векторов, а поведение другого будет аналогичным.
Вид поляризации волны определяется видом той кривой, которую описывает электрический вектор Е волны за один период колебания в
плоскости наблюдения. При этом свет должен распространяться к наблюдателю. Плоскость наблюдения – это плоскость, перпендикулярная направлению распространения волны (см . Рис.1). Ясно, что магнитный векторВволны описывает такую же по форме кривую, что и вектор Е.
1.Линейная (плоская ) поляризация-в процессе распространения волны вектор Е колеблется все время в одной и той же пространственной плоскости (см. Рис.1), которую называют плоскостью колебаний вектора Е (иногда также плоскостью поляризации волны). Проекция вектора Е на плоскость наблюдения в этом случае будет иметь вид отрезка прямой линии, в связи с чем эту поляризацию и называют линейной или же плоской. Отметим, что плоскость колебания магнитного вектора волны будет перпендикулярна плоскости колебаний вектора
Е
2.Круговая (циркулярная) поляризация: - при такой поляризации вектор Е волны за один период волны делает полный оборот вокруг направления распространения волны, при этом его длина остается постоянной. В плоскости наблюдения проекция вектора Е описывает круг, что и определяет название такой поляризации. Если вектор вращается по часовой стрелке (волна должна
распространяться к наблюдателю), то поляризация называется правой круговой,
72 а
если против часовой стрелки – то левой круговой поляризацией.
3. Эллиптическая поляризация - при этой поляризации вектор Е волны за один период волны тоже делает полный оборот вокруг направления распространения волны, но длина вектора Е при этом изменяется таким
образом, что конец его описывает в плоскости наблюдения эллипс. . Если вектор Е вращается по часовой стрелке , то поляризация называется правой, а если против – левой эллиптичной.
73
28. ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД ПРИ ПАДЕНИИ НОРМАЛЬНОПОЛЯРИЗОВАННОЙ ПЛОСКОЙ ВОЛНЫ. ЗАКОНЫ СНЕЛЛИУСА. КОЭФФИЦИЕНТЫ ФРЕНЕЛЯ.
Первый закон Снеллиуса: θ = θ1 ("уголпадения равен углу отражения").
Второй закон Снеллиуса: ("Отношение синуса угла преломления к синусу угла падения равно относительному показателю преломления сред n12").
74
75
30. ПОЛНОЕ ПРОХОЖДЕНИЕ ВОЛНЫ ВО ВТОРУЮ СРЕДУ
При определенных условиях падающая волна без отражения полностью проходит во вторую среду. Угол падения, соответствующий этому случаю, называют углом Брюстера. Условия, при которых отсутствует отраженная волна,
могут быть установлены путем решения уравнений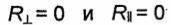 
относительно угла падения θ. В частном случае, когда обе среды являются
немагнитными диэлектриками, угол Брюстера θ Бр легко находится из физических соображений.
Пусть параллельно поляризованная волна падает на плоскую границу
раздела двух немагнитных диэлектриков
Под воздействием поля преломленной волны вторая среда поляризуется: дипольные моменты молекул второй среды ориентируются параллельно вектору напряженности электрического поля преломленной волны (рис.7.5).Упорядочение ориентированные молекулярные диполи второй среды излучают электромагнитные волны, суперпозиция которых и образует в первой среде плоскую отраженную волну. Молекулярный диполь (его можно считать элементарным электрическим вибратором) не излучает вдоль своей оси. Следовательно, отраженная волна не сможет возникнуть, если оси упорядоченно ориентированных молекулярных диполей будут параллельны направлению, в котором должна распространяться отраженная волна. Указанная ориентация молекулярных диполей имеет место при выполнении условия θ + θ= π/2, из которого следует, что cos θ =
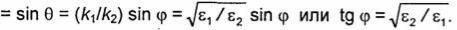Таким образом, в
рассматриваемом случае 
плоская параллельно поляризованная волна целиком проходит во вторую среду при угле падения
В случае нормальной поляризации молекулярные диполи ориентируются перпендикулярно плоскости падения и, следовательно, перпендикулярно направлению распространения отраженной волны. Перпендикулярно своей оси молекулярный диполь (ЭЭВ) излучает одинаково во всех направлениях. Поэтому
в данном случае угла Брюстера не существует: от границы раздела двух
76
немагнитных диэлектриков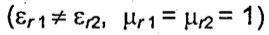 
нормально поляризованная волна отражается при любом угле падения.
Используя перестановочную двойственность уравнений Максвелла, легко
показать, что в случае сред, у которых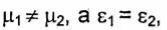 
отражение отсутствует при падении нормально поляризованной волны под углом
Параллельно поляризованная волна в этом случае отражается при любом угле падения.
Анализ возможности полного прохождения волны во вторую среду в более общем случае, когда и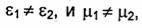 
может быть
проведен на основе решения уравнений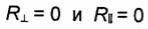 
относительно cos θ.
Плоские волны круговой и эллиптической поляризации (см. 6.2) можно представить в виде суперпозиции двух линейно поляризованных плоских волн, одна из которых поляризована нормально, а другая - параллельно плоскости падения. Так как условия существования угла Брюстера для параллельной и нормальной поляризаций различны, то волны с круговой и эллиптической
поляризациями будут отражаться при любых углах падения 
Однако при этом соотношение между амплитудами нормальной и параллельной составляющих в отраженной и преломленной волнах будет иным, чем в падающей волне. Это приводит к изменению поляризации отраженной и преломленной волн по сравнению с падающей. В частности, если плоская волна с круговой поляризацией падает под углом Брюстера для одной из двух образующих ее линейно поляризованных волн, то отраженная волна оказывается линейно поляризованной, а преломленная - эллиптически поляризованной
.
77
31. ПОЛНОЕ ОТРАЖЕНИЕ ПРИ ПАДЕНИИ ПЛОСКОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД. СТРУКТУРА ПОЛЯ. ОСНОВНЫЕ СВОЙСТВА. ПОНЯТИЕ О НАПРАВЛЕННЫХ ВОЛНАХ. ВОЛНЫ ТИПА Н И Е.
Полное отражение электромагнитной волны происходит от
поверхности идеально проводящей 
. В этом случае
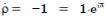и амплитуда волны при отражении не изменяется. Знак ―—‖ для коэффициента отражения означает, что фаза волны электрического поля в плоскости отражения изменяется на 180°, а фаза волны магнитного поля
остается неизменной (вторые слагаемые для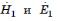 
в
отличаютсязнаком).В результате наложения падающих и отраженных волн перед поверхностью отражения образуется так называемая ―стоячая‖ волна. Особенности этого явления можно понять, рассматривая аналитическое
выражение (4.3,а) для случая 
и для упрощения α = 0 ( γ= k). Восстанавливая временной множитель exp(iωt) и оставляя действительную часть, получим
(4.5)
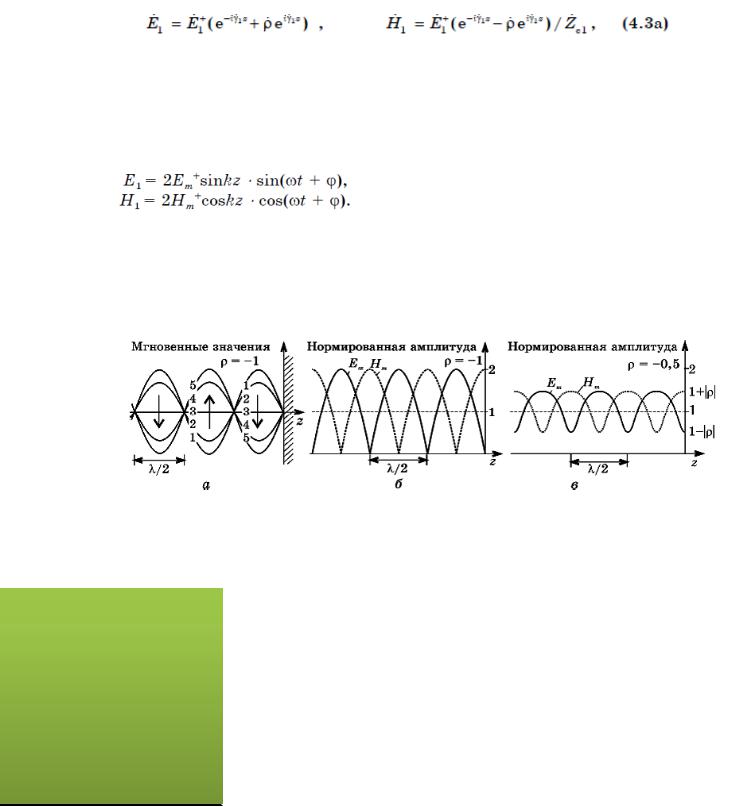
Данные выражения описывают не волновой процесс, а гармонические колебания, амплитуда и фаза которых зависят от продольной координаты. Мгновенные ―фотографии‖ этих колебаний, изображенные на рис. 4.2,а, сделаны через промежутки времениТ/8 и напоминают колебания струны. В границах одного полупериода колебания происходят синфазно, но амплитуда их в разных точках разная.
Рис. 4.2. Пространственное распределение мгновенных значений колебаний (а) и их амплитуд (б) при полном отражении (ρ = —1) и (в) частичном (ρ = —0,5): сплошные линии для электрического поля, штриховые — для магнитных. Распределение амплитуды, нормированной к амплитуде падающей волны, показано на рис. 4.2,б. Характерной особенностью является наличие ―узлов‖, то есть точек с нулевой амплитудой, и ―пучностей‖, где амплитуда максимальна и вдвое превышает амплитуду падающей волны. Причем положение этих точек в пространстве постоянно, что и объясняет используемое название — стоячая волна. Причину такой ситуации понять нетрудно — узлы образуются в тех точках, где падающая и отраженная волны встречаются в противофазе. Для электрического поля ―узлы‖ расположены на расстояниях, кратных половине
78 длины волны, так как на этих расстояниях ―набег― фазы при прохождении волны туда и обратно составляет целое число периодов, а
противофазностьобеспечивается сдвигом фазы на 180° при отражении. Поскольку для магнитного поля фаза при отражении не изменяется, то в тех же точках падающая и отраженная магнитные волны будут встречаться синфазно и образовывать ―пучности‖. Легко представить, что между двумя соседними ―узлами‖ электрического поля будут расположены ―узлы‖ магнитного и наоборот. Подобное явление наблюдается и при неполном отражении. Для описания процессов в общем случае, когда 0 ≤ | ρ| <1, можно представить выражения (4.3) для полей над поверхностью отражения, восстановив для наглядности временной множитель exp(iωt) и считая γ= k (потери отсутствуют), в виде:
(4.6)
Такая форма записи в отличие от (4.3), где поля представлены как сумма падающей и отраженной волны, отвечает только одной волне, падающей, но с
амплитудой, изменяющейся в зависимости от координаты (величину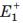 
считаем действительной):
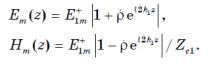(4.7)
Эти функции периодичны в пространстве и приобретают максимальные значения, в (1 + | ρ|) раз большие, чем амплитуда падающей волны, в точках, называемых ―пучностями‖. Между ними находятся ―узлы‖, где амплитуда минимальна и составляет (1 — | ρ|) от амплитуды падающей волны. Со временемпространственное положение этих точек не изменяется, поэтому для процессов, описываемых выражениями (4.6), и используют название ―стоячая волна‖.
Графики распределения амплитуд электрического и магнитного полей (рис. 4.2,в) полностью совпадают с графиками для амплитуд соответственно напряжения и тока в длинной линии передачи (см. разд. 3.4). Укажем также, что выражения для коэффициентов отражения электромагнитной волны от границы раздела сред и волны напряжения от нагрузки в длинной линии являются подобными при условии соответствующей замены величин. Такая аналогия связана с тем, что эти процессы описываются фактически одинаковыми волновыми уравнениями. Для углубления этой аналогии рассмотрим, как изменяются комплексные амплитуды электрического и магнитного полей при прохождении волной некоторого расстояния между точками z1 и z2 (рис. 4.3). Запишем выражения для полей соответственно в этих точках в виде сумм падающей и отраженной волн:
(4.8)
С помощью тождественных преобразований, исключив из этих выражений амплитуды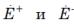 
, получим выражения для
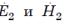через амплитуды 
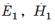и расстояние z = z2—z1:
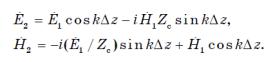(4.9)
79