
EMPiV
.pdf
10

10

10

41. ВОЛНЫ ТИПА Н В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ. КЛАССИФИКАЦИЯ, ОСНОВНЫЕ СВОЙСТВА.
Структура магнитного и электрического полей в прямоугольном волноводе для основной волны типа Н.
На практике наибольшее распространение получили волны Н-типа, в частности, основной тип волны – волна Н10. Заметим, волна Н-типа для волновода прямоугольного сечения записывается в виде Нmn, где m,n – индексы, указывающие на количество полуволн вдоль оси х и у соответственно.
Минимальная частота основной волны в прямоугольном волноводе типа H10, способной распространяться в волноводе, равна: С2 , где — скорость света в волноводе, a — размер
широкой стенки волновода.
Свойства волны. Как уже отмечалось, при а>bосновной волной прямоугольного волновода является волна H10. Она имеет наибольшую критическую длину волны, равную 2а. На заданной частоте размеры поперечного сечения волновода, при которых возможна передача энергии по прямоугольному волноводу, для этой волны можно выбрать наименьшими.
10
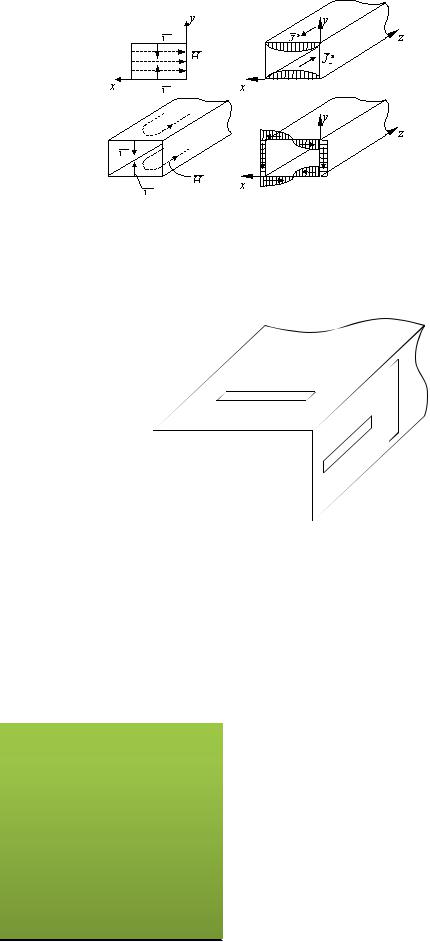
42.СТРУКТУРА ПОЛЕЙ ВОЛН ТИПА Н10, Н01, Н11
Токи проводимости в стенках волновода всегда протекают в направлении, перпендикулярном вектору напряженности магнитного поля у стенки.
Токи в прямоугольном волноводе при распространении волны H10
Щели:
Если щель пересекает линии поверхностного тока, то она – излучающая. Если щель прорезана параллельно линиям тока, то она является неизлучающей.
3 |
2 |
|
Излучающие и неизлучающие щели.
Структура поля волны H10:
|
|
hH |
|
x |
)e jhz , Ex |
|
|||
H x j |
|
g |
2 |
0 sin( |
a |
0, |
|||
|
|
|
|
|
|
|
|
||
|
|
H |
|
x |
|
|
|||
|
|
|
|
|
|
||||
E y j |
|
|
0 0 |
sin( )e jhz |
, H y 0, |
||||
|
|
|
|
ag 2 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
H z H 0 cos( x )e jhz , Ez |
0. |
|
|||||||
|
|
|
|
|
a |
|
|
|
|
10На рисунке

10

43. ВОЛНЫ ТИПА Е В ПРЯМОУГОЛЬНОМ ВОЛНОВОДЕ
Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения (рис. 10.1). Предположим, что стенки волновода обладают бесконечной проводимостью, а заполняющая его среда - идеальный диэлектрик с параметрами ε и μ. В такой направляющей системе могут существовать волны Е и Н и не могут существовать TЕМ-волны (см. 9.4). На рис. 10.1 показаны используемая система координат и размеры а и b поперечного сечения волновода. Для определенности будем считать, что а ≥ b, а источники, создающие поле, расположены со стороны отрицательных значений переменной z за пределами рассматриваемой части линии передачи (созданная ими волна распространяется в положительном направлении оси Z). При а > b стенки с поперечными размерами а и b будем называть соответственно широкой и узкой стенками прямоугольного волновода.
Так как поперечные составляющие векторов поля выражаются через продольные (см. 9.2), то для вычисления поля волн Е и Н достаточно определить составляющую Еmz или Нтг соответственно. Составляющие Ётz и Нтz удовлетворяют уравнению Гельмгольца
где функция w равна Emz для Е-волн и Hmzдля H-волн, - ко-эффициент фазы рассматриваемой волны. Правая часть уравнения (10.1) равна нулю, так как по предположению сторонние источники расположены за пределами рассматриваемой части волновода. Фактически задача состоит в нахождении так называемых собственных волн прямоугольного волновода.
Для решения уравнения (10.1) применим метод разделения переменных.
Запишем функцию w в виде w= w(x, у, z, t) = = w°(x, y)exp[i(ωt- β z)]. Очевидно, что функция w°(x, y) также удовлетворяет уравнению (10.1). Представим ее в виде произведения двух функций, каждая из которых зависит только от одной переменной: 217
Отметим, что в случае Е-волн значения т = 0и n = 0 не годятся, так как при этом случае Emz = 0 во всех точках внутри волновода.
10 |
Поперечные составляющие векторов поля выражаются через Emz |
|
|
|
соотношениями (9.19) и (9.20). Введем обозначение А•С = = EOz и выпишем |

окончательные выражения для составляющих векторов поля Е-волн в прямоугольном волноводе: 218
Отметим, что в случае Е-волн значения т = 0и n = 0 не годятся, так как
Emz = 0 во всех точках внутри волновода.
Поперечные составляющие векторов поля выражаются через Emzсоотнош
(9.20). Введем обозначение А•С = = EOz и выпишем окончательные
10

составляющих векторов поля Е-волн в прямоугольном волноводе:
Подчеркнем, что индекс т в формулах (10.10а) и (10.106) имеет совершенно разный смысл. В (10.10а) он указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в (10.106) индекс т - натуральное число, определяющее значение постоянной γх, как это следует из формулы
(10.9).
Значение постоянной у± находится из формул (10.4) и (10.9):
Коэффициент фазы р вычисляется по формуле (9.14).
Таким образом, все параметры, входящие в формулы для поля Е-волн, кроме постоянной Е0z определены. При той постановке задачи, которая была здесь использована, постояннуюEOz определить нельзя. Для ее нахождения требуются дополнительные данные: либо более конкретные сведения об источнике, создающем рассматриваемую волну, либо значение какой-нибудь составляющей векторов поля в точке, где эта составляющая отлична от нуля, либо задание мощности бегущей волны (т.е. задание среднего за период значения потока энергии через поперечное сечение волновода, соответствующего рассматриваемой волне). Для анализа вопросов, изучаемых в данной главе, конкретное значение посто-яннойEOz не требуется.
Прежде чем перейдем к анализу свойств поля Е-волн, описываемого выражениями (10.10), выведем формулы для поля Н-волн в прямоугольном волноводе. Волны Е и Н имеют много общих черт, и их свойства удобно анализировать совместно.
В случае Н-волн (Hz≠0, Ёz=0) функция w = Hmz. Решение уравнения (10.1) строится так же, как для Е-волн. Изменяются только краевые условия. Требуя, чтобы касательные составляющие вектора Ё на стенках волновода обращались в нуль, имеем
10

Но искомой является функция w, поэтому выписанные краевые условия следует преобразовать в условия для функции w. Поперечные составляющие вектора Ет выражаются через Hmz соотношением (9.14). Из этого соотношения и краевых условий (10.13) после перехода к функции w°(x, y) получаем
В отличие от (10.9) в случае Н-волн индексы т и п могут принимать нулевые значения. Однако они не могут равняться нулю одновременно: при этом составляющая Нz не зависит от переменных х и у и вектор Ё будет тождественно равен нулю, что невозможно. Выпишем окончательные выражения для комплексных амплитуд составляющих векторов поля Н-волн в прямоугольном волноводе: 219
Аналогично случаю Е-волн в формулах (10.17а) индекс т указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в формулах (10.176) т связано с постоянной ух соотношением (10.16).
Составляющие векторов поля Н-волн найдены с точностью до произвольного постоянного множителя Hoz , определение которого в рамках выбранной электродинамической модели невозможно (см. аналогичное замечание, сделанное при анализе Е-волн).
Легко показать, что поперечное волновое число γ┴ и критическая длина волны λкр в случае Н-волн также определяются формулами (10.11) и (10.12) соответственно.
10
