EMPiV
.pdf
Подставляя соотношение (1.4) в (1.44), получаем εodiv E = ρ- div ρ. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов ρр, возникающих в результате неравномерной поляризации среды такие заряды поляризационные:
divP=-ρP. |
(1.45) |
Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем V, ограниченный поверхностью S. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8
объем ΔV показан пунктиром). Подчеркнем, что поляризационные заряды являются "связанными" и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из
определения вектора Р . Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к
соотношению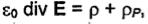 
из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды. Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля. Поток вектора В через любую замкнутую
поверхность S равен нулю, т.е. 
Это означает, что линии вектора Ввсегда пронизывают замкнутую поверхность S
(рис. 1.9).
Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме уравнения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим
div В = 0, |
(1.47) |
Уравнение (1.47) представляет собой четвертое уравнение Максвелла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.
10
4. КЛАССИФИКАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ЯВЛЕНИЙ
Система уравнений Максвелла охватывает всю совокупность электромагнитных явлений, относящихся к макроскопической электродинамике. В ряде частных случаев уравнения Максвелла упрощаются. Самым простым является случай, когда поле не зависит от 31 времени и, кроме того, отсутствует перемещение заряженных частиц (j = 0). При этих условиях система уравнений [1.52) и (1.53) распадается на две независимые системы:
Уравнения (1.55) содержат только векторы электрического поля, а (1.56)-только векторы магнитного поля. Это означает, что в данном случае электрические и магнитные явления независимы.
Явления, описываемые системой уравнений (1.55), принято называть электростатическими. Электростатические поля-это поля, созданные неподвижными, неизменными по величине зарядами. Система уравнений (1.55)
является полной системой дифференциальных уравнений электростатики.
Уравнения (1.56) характеризуют поля, создаваемые постоянными магнитами. Они также могут быть использованы для анализа свойств магнитного поля, созданного постоянными оками в области, в которой плотность тока проводимости равна нулю (j = 0) и которая не сцеплена с током (не охватывает его линий). Явления, описываемые системой (1.56), называют
магнитостатическими, а соотношения (1.56) - уравнениями магнитостатики.
При наличии постоянного тока электрическое и магнитное поля уже нельзя считать независимыми. Электромагнитное поле, созданное постоянными токами, называют стационарным электромагнитным полем. Система уравнений Максвелла в этом случае принимает вид
Вкачестве самостоятельного класса выделяют также так называемые квазистационарные процессы, т.е. процессы, протекающие достаточно медленно. В этом случае в первом уравнении Максвелла при наличии тoка проводимости можно пренебречь током смещения: rotH = j. Однако в тех случаях, когда токов проводимости нет (например, емкость в цепи переменного тока), токи смещения необходимо учитывать, при этом rot H =.- dDldt. Второе уравнение Максвелла при анализе квазистационарных процессов записывается в обычной форме: rotH =- dD/dt.
Вобщем случае используют полную систему уравнений Максвелла (1.52) и
(1.53).
Вслучае гармонических во времени колебаний систему (1.52) удается упростить с помощью искусственного приема, получившего название метода комплексных амплитуд.
11
5. УРАВНЕНИЯ МАКСВЕЛЛА В КОМПЛЕКСНОЙ ФОРМЕ
12
13
14
15
6. СТОРОННИЕ ИСТОЧНИКИ. УРАВНЕНИЯ МАКСВЕЛЛА С УЧЕТОМ СТОРОННИХ ИСТОЧНИКОВ.
Сторонними источниками электромагнитного поля являются заряды и токи, создаваемые батареями и генераторами. Для случая переменных полей сторонними (первичными) источниками являются токи в антенне. Сторонние токи и заряды учитываются в системе уравнений Максвелла путем суммирования соответствующих токов и зарядов
Первое уравнение Максвелла
= + |
|
+ ст |
(1) |
|
|
||||
|
|
|
где ст- плотность сторонних токов в рассматриваемой точке пространства, a j - как и прежде, плотность тока проводимости, вызванного электромагнитным полем: j = ζЕ.
Аналогично сторонним токам вводится понятие сторонних зарядов. Они учитываются в третьем уравнении Максвелла:
= + ст (2)
где ст- объемная плотность сторонних зарядов.
Второе и четвертое уравнения Максвелла остаются без изменений. В случае переменных полей функции ст стсвязаны уравнением непрерывности
ст + |
ст |
= 0 (3) |
|
|
|||
|
|
16
УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ МОНОХРОМАТИЧЕСКОГО ПОЛЯ В ОДНОРОДНОЙ СРЕДЕ, УЧИТЫВАЮЩИЕ СТОРОННИЕИСТОЧНИКИ:
17
7. ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Если проводник неоднороден по своему составу и/или имеет неодинаковое сечение, то для характеристики тока в различных частях проводника используют закон Ома в дифференциальной форме. Для его вывода выделим внутри проводника элементарный цилиндрический объем (рис.1) с образующими, параллельными вектору плотности тока . Если выделенный объем достаточно мал, его можно считать однородным и применить к нему закон Ома:
= , где
=
= =
=
=
Или в векторном виде:
=
Величина = называется коэффициентом
электропроводности или проводимостью материала. Единицей измерения в СИ является См (сименс).
18
8. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ. ЗАКОН СОХРАНЕНИЯ ЗАРЯДА.
Первое уравнение Максвелла в дифференциальной форме
= + |
|
(1) |
|
|
|||
|
|
Третье уравнение Максвелла в дифференциальной форме
= . |
(2) |
|||
D -вектор электрической индукции. |
||||
Возьмем Дивергенцию от обеих частей равенства (1). Учитывая, что |
||||
дивергенция любого ротора равна нулю и используя уравнение (2) |
||||
получим |
|
|
||
+ |
|
= – Уравнение непрерывности. (3) |
||
|
||||
|
|
|
|
|
Правая часть уравнения (1) представляет собой сумму плотностей |
||||
тока проводимости и тока смещения, т.е. плотность полного тока |
||||
полн = + |
|
поэтому уравнение (2) эквивалентно условию |
||
|
||||
|
|
|
|
|
|
полн = . Равенство нулю дивергенции какого-либо вектора |
|||
|
означает непрерывность линий этого вектора. Следовательно, |
|||
|
уравнение (2) показывает, что линии плотности полного тока |
|||
|
являются непрерывными, в то время как линии плотностей токов |
|||
|
проводимости и смещения могут иметь начало и конец. Например, |
|||
|
линии плотности тока проводимости начинаются в тех точках |
|||
|
пространства, где плотность зарядов уменьшается, и оканчиваются |
|||
|
там, где плотность зарядов возрастает. |
|||
|
Уравнение (1) связано с законом сохранения заряда и по существу |
|||
|
является его дифференциальной формой. Закон сохранения заряда |
|||
|
можно сформулировать следующим образом. Всякому изменению |
|||
|
величины заряда, распределенного в некоторой области, |
|||
|
соответствует электрический ток /, втекающий в эту область или |
|||
|
вытекающий из нее: |
|||
|
= − |
|
|
|
19 |
|
|||
|
||||
|
|
|||