Постановка задачи

Дано:

1. X(t) = A(t)cos(t) – узкополосный центрированный стационарный нормальный СП (на выходе ПФ),

2. .

Определить:

1. w(A) – одномерную плотность вероятности огибающей,

2. w() – одномерную плотность вероятности фазы.

Для решения этой задачи наметим три этапа:

1. Переход к аналитическому СП и определение совместной плотности вероятности.

2. Расчет совместной плотности вероятности по вычисленной на первом этапеи связямA(t), (t) с (5.3) ÷ (5.6) .

3. Определение одномерных плотностей вероятности w(A) и w() по вычисленной совместной плотности вероятности .

Решение

1 этап. Найдем одномерную плотность вероятности процесса. На основе линейности преобразования Гильбертаделаем вывод о том, что– нормальный СП. Далее, учитывая, что, получаем, а следовательно

.

Таким образом, имеем

.

Докажем некоррелированность в совпадающие моменты времени, т. е. что.

.

После подстановки ,,, учитывая, что при, получим

.

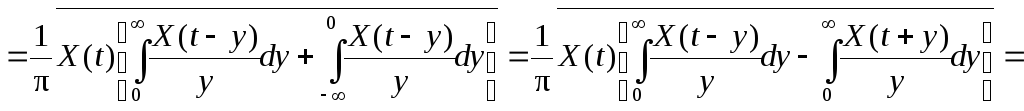
Некоррелированность сечений нормальных процессов влечет их независимость, следовательно

.

2 этап. Расчет совместной плотности вероятности

,

где согласно (5.2), (5.5) и (5.6)

.

Следовательно, с учетом (5.3) имеем

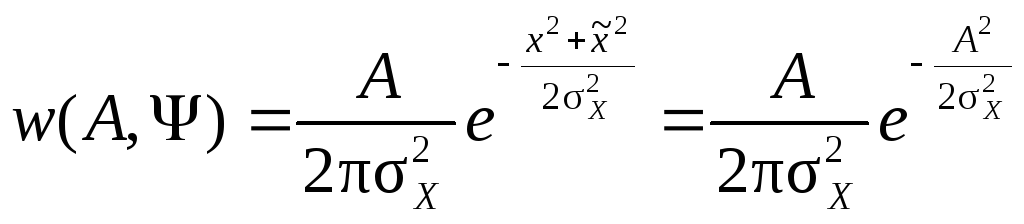. (5.7)

3 этап. Определение одномерных плотностей вероятности

,

Окончательно

, (5.8)

. (5.9)

Выражение (5.8) известно как распределение Рэлея, его график приведен на рис. 5.8. На рис. 5.9 приведен график равномерного распределения фазы (5.9).

Выражение (5.7) можно представить в виде произведения (5.8) и (5.9)

,

из чего следует независимость огибающей A(t) и фазы w() нормального СП.

Рассмотрим более сложную задачу прохождения аддитивной смеси выше рассмотренного нормального СП с гармоническим сигналом через АД и ФД. Постановка задачи сохраняется прежней за исключением исходного процесса Y(t) , который приобретает вид

,

где X(t) – центрированный нормальный СП.

Поскольку

,

то

.

Запишем Y(t) в квазигармонической форме

и будем решать задачу определения плотностей вероятности w(A) и w() по выше приведенному плану.

Предварительно запишем X(t) в квазигармонической форме и через его квадратурные компоненты

.

Тогда

,

где

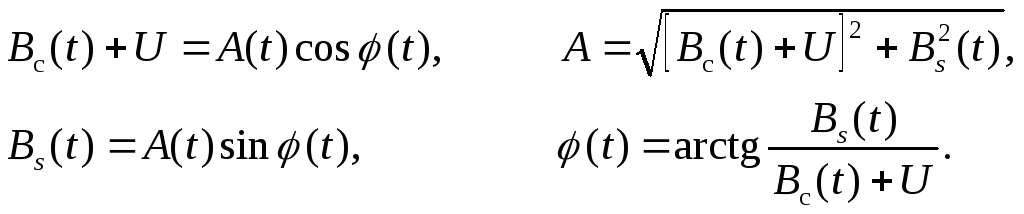
Отсюда

, (5.10)

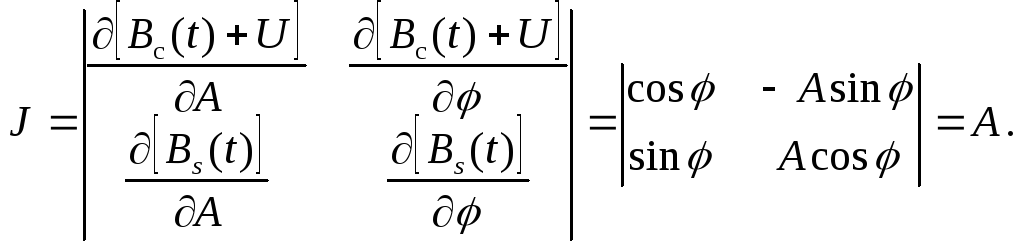(5.11)

Для нахождения обратимся к аналитическому СП

.

Из его выражения видно, что являются линейными преобразованиями центрированного нормального СПX(t):

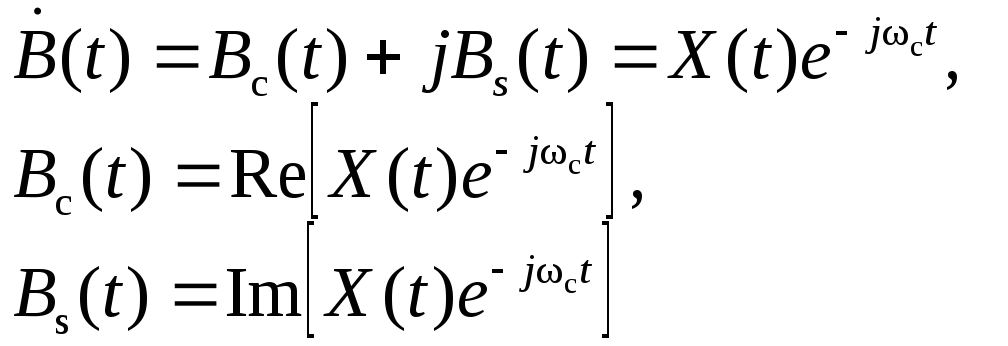
и, следовательно, имеют нормальное распределение с дисперсиями

.

Докажем их некоррелированность (а следовательно и независимость) в совпадающие моменты времени

.

Здесь учтено, что B(t) и θ(t) – огибающая и фаза нормального СП являются, как выше установлено, независимыми.

Таким образом,

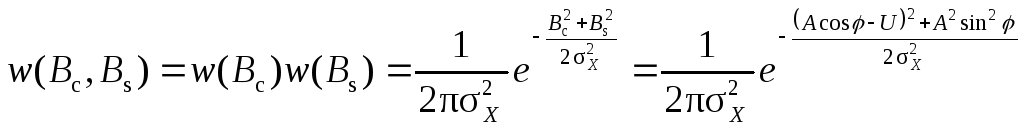
и с учетом (5.10) и (5.11) получаем

. (5.12)

Поскольку выражение (5.12) невозможно представить в виде произведения одномерных функций , то можно сделать вывод о зависимости процессов.

Для нахождения распределения огибающей суммы центрированного нормального СП с гармоническим сигналом проинтегрируем (5.12) по всем возможным значениям случайной фазы (t)

.

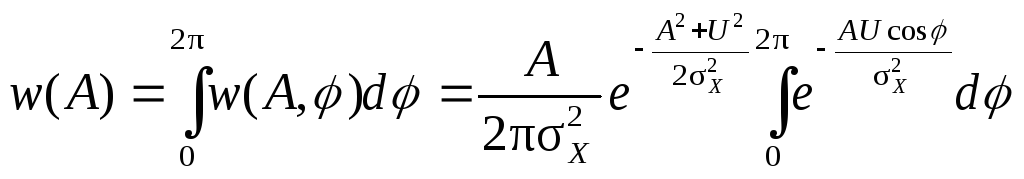Интеграл вида

известен в математике как модифицированная функция Бесселя нулевого порядка. С его учетом окончательно имеем

. (5.13)

Выражение (5.13) называют обобщенным распределением Рэлея или распределением Райса. Графики этого выражения приведены на рис. 5.10 для следующих частных случаев:

1. U = 0 – обычное распределение Рэлея,

2. –случай отсутствия в Y(t) СП X(t),

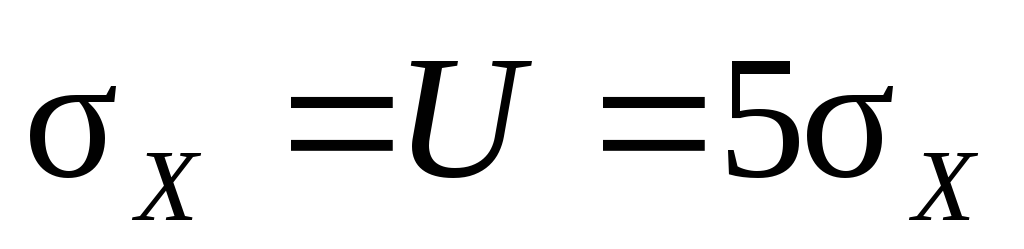
3. –обобщенное распределение Рэлея (Райса).

Из графиков видно, что чем больше отношение сигнал/шум тем правее смещен максимум плотности вероятности и тем симметричнее (ближе к нормальному распределению) кривая.

Выводы

1. Если мгновенные значения центрированного СП X(t) имеют нормальное распределение, то его огибающая A(t) распределена по закону Релея

,

а фаза (t) равномерно

.

2. Распределение огибающей аддитивной смеси центрированного нормального СП и гармонического сигнала подчиняется обобщенному распределению Рэлея (оно же распределение Райса)

.