Рекомендации по проведению экспериментальных исследований случайных процессов

Для закрепления полученных при изучении раздела 4 знаний на базе виртуальной лаборатории можно провести экспериментальные исследования случайных процессов используя:

• осциллограф – для наблюдения реализаций СП во временной области,

• анализатор спектра – для наблюдения реализаций СП в частотной области,

• анализатор уровней – для наблюдения плотности вероятности,

• коррелометр – для наблюдения корреляционных функций.

Целесообразно работать в рамках конфигурации лабораторного стола по темам работ №2 и №19. Источником СП с равномерным и нормальным распределением может служить генератор сигнала (в режиме генератора шума) (рис. 4.9) и соответствующие подпункты меню «Сигналы» (рис. 4.10).

Рекомендуется выполнить лабораторную работу №19 в полном объеме (рис. 4.10). Обратите внимание на связь размеров «шумовой дорожки» на экране осциллографа с эффективным значением шума и на связь корреляционных характеристик с энергетическими спектрами случайных процессов.

5. Прохождение случайных процессов через преобразователи сигналов

Вобщем случае решение задачи прохождения заданного СП через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определениеn-мерной плотности вероятности (или функции распределения) реакции цепи Y(t) на заданное случайное воздействие X(t) (рис. 5.1). Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев.

5.1. Прохождение случайных процессов через безынерционные цепи

Безынерционная цепь (безынерционный функциональный узел –БФУ) полностью описывается функциональной зависимостью y = f(x), связывающей мгновенные значения воздействия x(t) и реакции y(t) в совпадающие моменты времени. В результате имеем дело с функциональным преобразованием случайного процесса Y(t) = f [X(t)].

Для вычисления одномерной плотности вероятности реакции w(y) по известной плотности вероятности воздействия w(x) рассмотрим рис. 5.2, на котором изображены функциональная характеристика БФУ y = f (x), заданная плотность вероятности воздействия w(x) и искомая плотность вероятности реакции БФУ w(y). Учитывая, что при попадании случайной величины X в интервал (x, x+dx) случайная величина Y с вероятностью 1 попадает в соответствующий ему интервал (y, y+dy), можно написать следующее соотношение

,

из которого вытекает

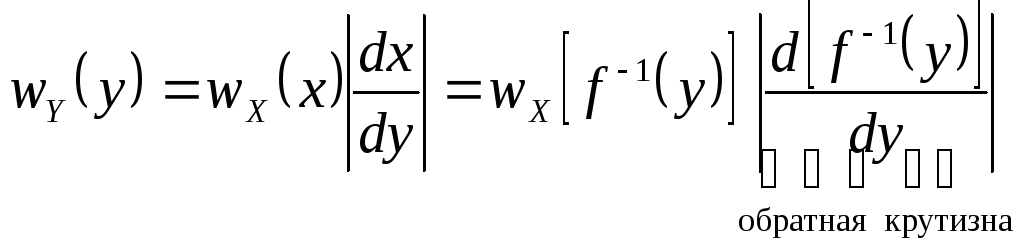, (5.1)

где f ^-1(y) – обратная функция (x = x(y) = f ^-1(y)).

Дифференциалыdx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности.

Примеры:

1. Линейное безынерционное преобразование y = f (x) = ax + b.

Обратная функция ,

.

Таким образом, при линейном преобразовании случайной величины ее кривая плотности распределения смещается на величину b, а масштаб по координатным осям изменяется в |a| раз.

2. Кусочно-линейное преобразование y = f (x) (рис. 5.3).

Задачу решим графически, определяя вид кривой w_Y(y) на отдельных интервалах оси у.

И

y y

y₂

y₁

x₁ x₂ x 0 w(y)

w(x)

x₁ x₂ x

Рис. 5.3. Кусочно-линейное преобразование случайной величины.

з рассмотрения функциональной характеристикиy = f (x) с очевидностью вытекает, что

а) при у < 0 и у > y₂ w_Y (y) = 0, т. к. значения реакции у не могут выйти за пределы уровней отсечки (у = 0) и насыщения (у = y₂,);

б) при 0 < у < y₁ w_Y (y) = 0, т. к. в этот интервал (протяженностью y₁) значения реакции попадают при единственном значении воздействия x = x₁, вероятность которого w_X(x₁)dx  0;

в) при y₁ ≤ у < y₂ , гдеb = y₁, (см. пример 1);

г) при у = 0 , т. к.у = 0 для всех х < x₁;

д) при у = у₂ , т. к.у = у₂ для всех х > x₂.

3. Преобразование при неоднозначной обратной функции

.

На практике встречаются ситуации, когда обратная функциональная характеристика является многозначной (рис. 5. 4). Рассуждая аналогично тому, как это делали при выводе выражения (5.1), легко убедиться в том, что в этом случае для интервала

.

Если при анализе прохождения СП через БФУ достаточно знать только основные характеристики распределения реакции, то их можно найти, не определяяw_Y(y). В частности:

математическое ожидание

,

дисперсия

функция корреляции

.