Примеры энергетических спектров некоторых стационарных сп:

1. Квазибелый шум N_F(t)

Энергетический спектр такого процесса () равномерен в ограниченной полосе частот (–F, +F) (рис. 4.3).

К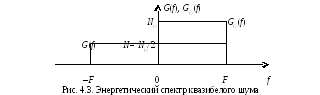орреляционная функция квазибелого шума имеет вид (рис. 4. 4)

.

Из полученного результата вытекает некоррелированность отсчетов квазибелого шума, взятых через интервалы времениk/2F. Для нормального процесса эти отсчеты оказываются еще и независимыми.

2. Белый шум N(t)

Энергетический спектр белого шума () равномерен в бесконечной полосе частот (рис. 4.5).

Корреляционная функция белого шума (рис. 4.6)

,

здесь использовано одно из определений дельта-функции

.

Из этих результатов вытекает статистическая независимость любых сколь угодно близких сечений такого процесса и его неограниченная дисперсия (мощность)

.

3. Синхронный телеграфный сигнал X(t)

С

x(t)

h

0 T t₁ t₂=t₁+ t

t

-h

Рис. 4.7. К расчету корреляционной функции телеграфного сигнала

инхронный телеграфный сигнал (CТС) представляет собой стационарный дискретный случайный процесс, принимающий на тактовых интервалах длительностью Т значения +h с вероятностью Р(0) или –h с вероятностью Р(1). Возможная реализация такого процесса показана на рис. 4.7.

Вычислим корреляционную функцию СТС, исходя из ее определения

,

где

.

В силу стационарности и при Р(0) = Р(1) = 0,5 имеем == 0 и

Далее учтем, что произведение , если, гдевременной интервал от сеченияt₁ до ближайшей границы такта (сечения принадлежат одному тактовому интервалу). В противном случае (при )

,

где Р(0/0), Р(0/1), Р(1/0) и Р(1/1) – переходные вероятности передачи символов в соседних тактовых интервалах, которые будем считать одинаковыми.

Таким образом

,

где – плотность вероятности временного интервала. Окончательно, учитывая свойство четности корреляционной функции стационарного процесса, получим

.

По полученной корреляционной функции несложно рассчитать энергетический спектр синхронного телеграфного сигнала (4.2)

.

Графики корреляционной функции и энергетического спектра синхронного телеграфного сигнала приведены на рис. 4.8.

Контрольные вопросы

1. Дайте определение случайного процесса (СП).

2. Каким образом дают исчерпывающее описание произвольного СП?

3. Каков смысл и размерность n-мерной функции распределения СП?

4. Каков смысл и размерность n-мерной плотности вероятности СП?

5. Как связаны функция распределения и плотность вероятности между собой?

6. Дайте определение математическому ожиданию СП и укажите его размерность и сущность как математического объекта.

7. Дайте определение дисперсии СП и укажите ее размерность и сущность как математического объекта.

8. Как осуществляют центрирование СП?

9. Определите функцию корреляции СП.

10. Какие СП называют стационарными в широком и узком смыслах?

11. Какие СП называют эргодическими?

12. Дайте определение постоянной составляющей СП, укажите ее размерность и сущность как математического объекта.

13. Дайте определение мощности СП, укажите ее размерность и сущность как математического объекта.

14. Какие СП называют нормальными (гуссовскими)?

15. Что понимают под временем корреляции СП?

16. Укажите основные свойства корреляционной функции стационарных СП?

17. Дайте определение спектральной плотности энергии СП и укажите ее размерность.

18. Дайте определение спектральной плотности мощности (энергетическому спектру) СП и укажите ее размерность.

19. Каковы связи между корреляционной функцией и энергетическим спектром стационарных СП?

20. Укажите основные свойства энергетического спектра стационарных СП.

21. Какой СП называют белым шумом? Укажите основные его свойства.

22. Какой СП называют квазибелым шумом? Укажите основные его свойства.

23. Какой СП называют синхронным телеграфным сигналом? Какова его корреляционная функция?

24. Как выглядит энергетический спектр синхронного телеграфного сигнала?