6.3. Синтез оптимального демодулятора при известном ансамбле сигналов (когерентный прием)

6.3.1. Постановка и решение задачи когерентного приема

на корреляторах

Постановка задачи:

Известны:

1. Ансамбль сигналов на выходе модулятора

{s_i(t)}; i = 1, 2,…, m; t  (0, T).

2. Непрерывный канал

,

где N(t) – квазибелый нормальный шум, т. е.

.

3. В качестве критерия качества приема задан критерий максимального правдоподобия (6.6)

Требуется синтезировать оптимальный демодулятор, иначе говоря, найти алгоритм оптимальной обработки входного сигнала и принятия решения о передаваемом сообщении.

Решение

В основу решения положим выражение заданного критерия качества приема, для чего рассмотрим входящие в него функции правдоподобия гипотез:

1) о наличии во входном колебании z(t) i-го сигнала [z(t) = s_i(t) + n(t)]

,

2) об отсутствии в нем какого-либо сигнала [z(t) = n(t)]

,

где .

Начнем с последней. Учитывая, что сечения квазибелого шума, разделенные интервалами , не коррелированны, а в силу нормального распределения шума и независимы, получим

.

Поскольку СП Z(t) = s_i(t)+ N(t) отличается от шума N(t) только известным, а потому неслучайным сигналом s_i(t), играющим роль математического ожидания Z(t), то

,

где использовано обозначение s_i,k = s_i(t_k).

В итоге отношение правдоподобия гипотез о наличии и отсутствии сигнала принимает вид

или с учетом

.

Перейдем к белому шуму, сняв ограничение на ширину его спектра (F  ). Иначе говоря, от евклидова пространства перейдем к гильбертовому. При этом

и

. (6.10)

Синтезируемый демодулятор должен принимать решение в пользу , обеспечивающего максимум выражения (6.10), или, что эквивалентно, максимум показателя экспоненты в нем

. (6.11)

Нетрудно видеть, что максимум (6.11) достигается при минимуме вычитаемого

. (6.12)

Демодулятор оптимальный по критерию максимального правдоподобия принимает решение в пользу того символа , сигналs_i(t) которого отстоит от принятого колебания z(t) на меньшее расстояние.

Рассматривая выражение (6.12) как алгоритм обработки принятого колебания z(t) приходим к схеме демодулятора, представленной на рис. 6.2.

Другую форму алгоритма можно получить из выражения (6.11)

,

или

, (6.13)

где E_i – энергия i-го сигнала.

Схема оптимального демодулятора, реализующего алгоритм (6.13), приведена на рис. 6.3. Поскольку в каждой ветви такого демодулятора присутствует вычислитель скалярного произведения – коррелятор, то его называют демодулятором на корреляторах (активных фильтрах).

Если использовать сигналы равных энергий, то алгоритм (6.13) и схема демодулятора (рис. 6.3) существенно упрощаются (рис. 6.4)

. (6.14)

Все вышерассмотренные демодуляторы используют всю информацию о форме сигналов s_i(t), включая начальную фазу. В каждой их ветви содержатся генераторы, генерирующие синфазные образцы этих сигналов, поэтому их называют когерентными демодуляторами.

6.3.2. Синтез оптимального когерентного демодулятора на согласованных фильтрах

Сохраняя постановку задачи синтеза демодулятора из предыдущего раздела и опираясь на алгоритмы (6.13) и (6.14), попробуем заменить коррелятор (активный фильтр), вычисляющий скалярные произведения приходящего колебания и образцов сигналов, на пассивный линейный фильтр, реализующий ту же операцию.

Как известно, реакция линейного фильтра на воздействие z(t) вычисляется с помощью интеграла Дюамеля

Потребуем, чтобы в заранее выбранный момент времени t₀ значение этой реакции y(t₀) с точностью до коэффициента совпало со скалярным произведением (6.14)

.

Как видно, это достигается при иt₀ ≥ T . После замены переменных получаем

. (6.15)

Фильтры, обладающие такими импульсными характеристиками, называют согласованными (СФ) с соответствующими сигналами.

На рис. 6.5 изображены сигнал длительностью Т и импульсные характеристики согласованных с ним фильтров для t₀ = Т и t₀ > Т, из которых видно, что импульсная характеристика согласованного фильтра является «зеркальным отражением» сигнала относительно момента времени 0,5t₀.

Т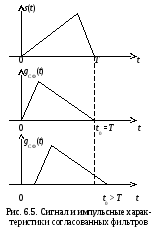аким образом, фильтры с импульсными характеристиками (6.15) вполне могут заменить корреляторы в ветвях оптимального демодулятора (рис. 6.3 и 6.4), если решения принимать по отсчетам их реакцииy_i(kT) (рис. 6.6).