18 Дәріс. Объекттер және сигналдардың динамикалық сипаттамаларын аппроксимациялауда негізделген идентификациялау әдістері
Дәрістің мазмұны:
- импульсті өтпелі функцияны тегістеу әдістері
Дәрістің мақсаты:
- объекттер және сигналдардың белгісіз динамикалық сипаттамаларын аналитикалық өрнектермен аппроксимациялауда негізделген идентифи-кациялау әдістерін оқу
Тегістелген импульсті өтпелі функцияны анықтау әдістерін қарастыруды жалғастырамыз.
18.1 Импульсті өтпелі және корреляциялық функцияларды бірге аппроксимациялауда негізделген идентификациялау әдісі
Объект сигналдарының корреляциялық функцияларын кейбір аппроксимациялау полиноммен алдын-ала тегістеп, жөндеу эффектісін алуға болады. Осы әдіс бойынша импульсті өтпелі функция (17.1) өрнегімен аппроксимацияланады, мұнда коэффициенттері (17.2) бойынша табылады. Сонымен бірге, Винер-Хопф теңдеуіне эквивалентті (16.5) алгебралық теңдеулер жүйесінің оң жағы да осы функциялармен аппроксимацияланады.
(18.1)
Теңдеулер саны белгісіздер санына тең болу үшін (17.1) және (18.1) өрнектерде аппроксимациялау функциялардың N саны бірдей болуы керек (сонда алынған жүйе квадратты болады).
(17.1)-ден өзгеше (18.1) өрнегінің
(18.2)
коэффициенттері берілген деп есептейміз, себебі өзара-корреляциялық Ryx(t) функцияның мәндері түйіндерде берілген, ал {φ(τ)} функциялары белгілі.
Винер-Хопф теңдеуіне эквивалентті (16.5) алгебралық теңдеулер жүйесіне импульсті өтпелі функцияның (17.1) және өзара-корреляциялық функцияның (18.1) өрнектерін қоямыз; екі жағында φj(τ) көбейтіп, τ=0-ден τ=m-ға дейін қосындылаймыз
(18.3)
{φj(τ)} ортогонормалданған болғандықтан белгісіз akкоэффициенттері бойынша сызықты алгебралық теңдеулер жүйесін аламыз
(18.4)
мұнда 
(18.5)
Осы жүйені есептеп, (17.1) өрнек бойынша импульсті өтпелі функциясының бағасын анықтаймыз.
Бастапқы жүйеге қарағанда (18.4) жүйенің реті неғұрлым кіші және {φj(τ)} тегіс және реттері кіші функциялар болғандықтан, жүйе жақсы шартталған. Сондықтанқарапайым есептеулер көмегімен импульсті өтпелі функцияның бағаларын жеткілікті дәлдікпен анықтауға болады. Есептеу процесінде аппроксимациялайтын функциялардың санын таңдау алдында айтылып кеткен қиындықтары кездеседі.
18.2 Сигналдарды аппроксимациялауда негізделген
идентификациялау әдісі
Егер де объекттің кірістегі және шығыстағы сигналдары кейбір аналитикалық өрнектермен аппроксимацияланатын болса, импульсті өтпелі функцияныда жийма интегралынан немесе Винер-Хопф теңдеуінен аналитикалық түрде алуға болады. Осы амалды іске асыруын қарастырайық. Объекттің кірістегі және шығыстағы сигналдары бақылау интервалында кейбір функцияларының сызықты комбинациясымен аппроксимацияланған. Ізделінетін импульсті өтпелі функцияны да осы функциялар жүйесімен аппроксимациялаймыз. Мысалы, сигналдар {pi(t)}ортогоналды полиномдар қатарларына жіктелген болсын
(18.6)
мұнда 
,
ал pij -
полином коэффициенттері.
Басқа сөзбен айтқанда сигналдар дәрежелі қатарлар түрінде көрсетіледі
(18.7)
мұнда коэффициенттері жіктеу коэффициенттерімен келесідей
байланысқан
Импульсті өтпелі функцияны да дәрежелі қатар ретінде іздейміз
(18.8)
(18.7) бен (18.8)-ды жийма интегралына қойып, келесіні аламыз
(18.9)
Бірдей дәрежедегі коэффициенттерін теңестіріп, (18.10)-ғы gi коэффициенттерін анықтауға алгебралық теңдеулер жүйесін аламыз. Нәтижесінде:
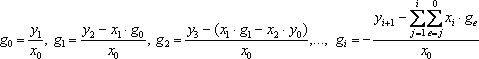
Комплексті кеңістікте аппроксимациялау есебі, яғни Лаплас бойынша жеңіл түрленетін ортогоналды функциялар қатарларымен көрсету қызық болып табылады. Осындай функциялар болып, мысалы, L(t) Лагерр функциялары табылады. Бұл кезде келесі бар
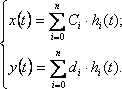(18.10)
(18.10) өрнектер комплексті кеңістікте келесідей жазылады
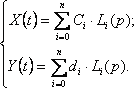
ал объекттің беріліс функциясының түрі
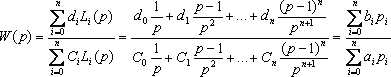
{an} және {ck} коэффициенттері арасында келесідей байланыстар бар
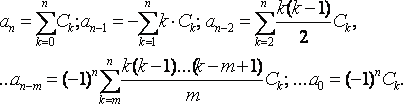
{bi} мен {di} арасындағы осы сияқты қатынастарды да алуға болады.
Егер де объект кірісіне берілетін сигнал үзікті–тұрақты сипат немесе функциясымен жеткілікті дәлдікпен аппроксимацияланатын болса, идентификациялау алгоритмі қарапайымдалады. Тұрақты мәні бар кірістегі сигналдың j-ші интервалы үшін келесіні жазуға болады
,
мұнда h(t) - өтпелі функция.
Белгілі ортнормалданған функциялар жүйесі бойынша осы функцияны жіктейік
Бұл кезде шығудағы сигналды да осы функциялар жүйесімен жіктеп, келесіні жазуға болады
,
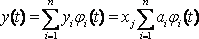осыдан аламыз:
Егер де кірістегі сигнал үзік-сызықты функциямен аппроксимацияланатын болса, осы амалды қолдануға болады.
Әдетте аппроксимациялайтын функцияларды таңдағанда олардың аз санында жақсы жуықтауды алу талабына сүйемелденеді. Идентификациялау есебін шешкенде кең қолданылатын кейбір полиномдарды атап кетейік.
Бастапқы Лагерр полиномдары (0, ∞) интервалында ω(t) = e-tсалмағымен ортонормалды болып табылады. n-ші ретті Лагерр полиномының түрі
(18.11)
бірінші үш полиномдар үшін өрнектері келесі болады
Келесі шарт орындалатындай
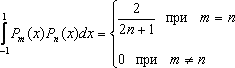
Лагерр полиномдары ортогоналды болады.
Нормалдыралғаннан кейін (18.21) өрнегі келесідей жазылады:
Аппроксимациялау функциялардың тағы да маңызды түрі [-1,1] интервалында ортогоналды болатын Лежандр полиномдары болады. n–ші Лежандр полиномы келесі өрнекпен бейнеленеді
Лежандрдың
бірінші полиномдарының түрі
Чебышев
полиномдары [-1,1] интервалында 
салмағымен
ортогоналды. n -ші ретті Чебышев
полиномының түрі
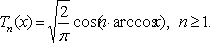
Бірінші полиномдары үшін өрнектер
f(x) функцияны Чебышев полиномдары жүйесі бойынша жіктегендегі коэффициенттері
.
Кез келген функцияны Чебышев полиномдарымен аппроксимациялап, қателіктің біртекті таратылуына және оның интервал соңғы шегінде жиналмауына қол жеткізуге болады.