Элементы прогнозирования и интерполяции. Моделирование временных рядов

Выявление и характеристика основной тенденции развития при иссле­довании динамики социально-экономических явлений дают основание для прогнозирования — определения будущих размеров уровня социально-эко­номических явлений.

Применение прогнозирования предполагает, что закономерность разви­тия, действующая в прошлом (внутри ряда динамики), сохраняется в про­гнозируемом будущем, т. е. прогноз основан на экстраполяции. Экстрапо­ляция, проводимая в будущее, называетсяперспективой, а в прошлое —ретроспективой.

Теоретической основой распространения тенденции на будущее являет­ся свойство социально-экономических явлений, называемое инерционностью. Именно инерционность позволяет выявить сложившиеся взаимосвязи как между уровнями динамического ряда, так и между группой связанных рядов динамики. На основе рядов динамики получаются весьма надежные прогнозы, если уровни ряда динамики сопоставимы и получены на основе единой методологии.

Применение экстраполяции в прогнозировании базируется на следую­щих условиях:

• развитие исследуемого явления в целом следует описывать плавной кривой;

• общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.

Временной горизонт экстраполяции не может быть бесконечным, потому что анализируемые временные ряды динамики нередко относительно короткие. Результат прогноза будет тем надежнее и точнее (при прочих равных условиях), чем короче срок экстраполяции (период упреждения).

Пусть имеется временной ряд {y₁,y₂, …,y_n}, взятый для простоты в равноотстоящие моменты времени. В качестве τ обозначим срок прогноза. В зависимости от принципов и исходных данных, положенных в основу прогноза, выделяют следующие элементарные методы экстраполяции:среднего абсолютного прироста, среднего темпа роста, экстраполяция на основе выравнивания рядов по какой-либо аналитической формуле.

1. С помощью среднего абсолютного прироста прогноз делается по следующей формуле:

где – средний абсолютный прирост

2. С помощью среднего темпа роста прогноз делается по следую­щей формуле:

где средний коэффициент роста наиболее хорош, когда общая тенден­ция ряда характеризуется экспоненциальной, показательной кривой.

3. Экстраполяция на основе выравнивания ряда по какой-либо кривой сводится к тому, что статистик выбирает некоторую кривуюу =f(t). Дан­ная кривая определена не только для каждого имеющегося момента времениt = 1,2, ...,п, но и для прогнозируемого момента времениt = п +τ.

Моделирование временных рядов

Следуя основной идее статистики, при анализе временного ряда его ви­димую изменчивость стараются разделить на закономерную ислучайную составляющие.

Закономерные изменения членов временного ряда подчиняются какому-то определенному правилу и поэтому предсказуемы. Эта составля­ющая может быть вычислена в каждый момент времени как некая функция от текущего момента времени. Эта функция может зависеть как от момента времени, так и от ряда других параметров. Когда эти параметры неизвест­ны, приходится оценивать их по имеющимся наблюдениям — как, например, бывает в случае регрессии.

Под закономерной (детерминированной) составляющей временно­го ряда {y₁, y₂, …, y_n} понимается числовая последовательность {d₁, d₂, ..., d_n}, элементы которой вычисляются по определенному правилу как функция времени.

Изменчивость, оставшаяся необъясненной, иррегулярна и хаотична и носит название случайной компоненты. Для ее описания необходим статистический подход. Если мы полностью выявили закономерную состав­ляющую в поведении временного ряда, то оставшаяся часть должнавыгля­деть хаотично и непредсказуемо. Ее обычно обозначают в следующем виде:{ε₁, ε₂, ...,ε_п}.

Другими словами, прогноз и моделирование временных рядов включает как этап анализа, или декомпозиции, так и этап синтеза, сборки ряда в единое целое. При проведении этапов анализа и синтеза ничто не должно остаться лишним и непроясненным; если это так, то можно говорить, что с точки зрения статистики о временном ряде нам известно все. К сожалению, в большинстве случаев этот идеал недостижим.

Остановимся более подробно на этапе анализа временного ряда. Раз­дают аддитивную имультипликативную модели анализа временного ряда. Формы разложения (декомпозиции) временного ряда на детерминированную и случайную составляющие различаются в этих моделях.

Аддитивной моделью временного ряда называется представление ряда в виде суммы детерминированной и случайной компонент, а именно: y_t = d_t + е_t, t= 1,2, ...,п.

Мультипликативной моделью временного ряда называется представление ряда в виде произведения детерминированной и случайной компонент, а именно: y_t = d_{t *} e_t, t= 1,2, ...,п.

Если в приведенном соотношении перейти к логарифмам, то получится аддитивная модель, но не для самих y_t, а для их логарифмов, т. е.. Это соотношение объясняет распространенность логарифмических шкал при анализе экономических временных рядов.

В рамках детерминированной компоненты определим тренд, сезонную и циклическую компоненты:

• тренд – tr_t,

• сезонную компоненту – s_t,

• циклическую компоненту – c_t.

Для определенности изложения рассмотрим аддитивную модель временного ряда (хотя это может быть и мультипликативная или какая-либо иная смешанная схема), т. е. возьмем представление вида:

d_t =tr_t + s_t + c_t.

В последнее время к указанным трем компонентам добавляют еще одну компоненту, именуемую интервенцией.

Под интервенциейпонимают существенное кратковременное воздействие на временной ряд.

Примером интервенции могут служить события «черного вторника» (11 октября 1994 г. курс доллара за день вырос на 40% с 283 рублей до 392 руб­лей), а также финансовый кризис августа 1998 г., когда курс рубля по отношению к доллару упал втрое.

К наиболее часто используемым моделям тренда относят следующие:

• линейная функция: ,

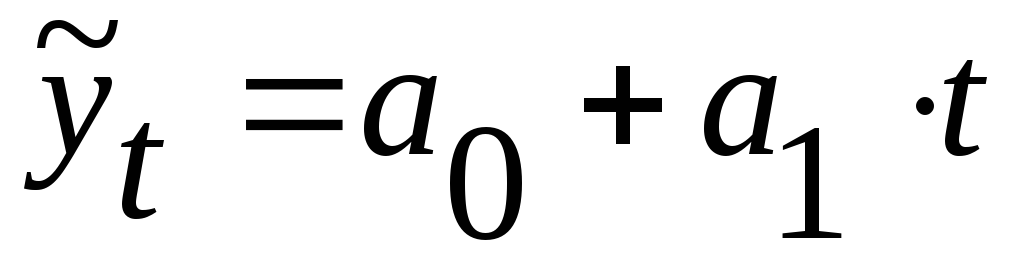• парабола: ,

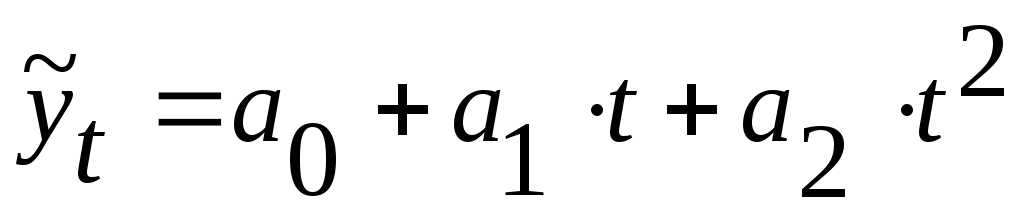• экспонента: .

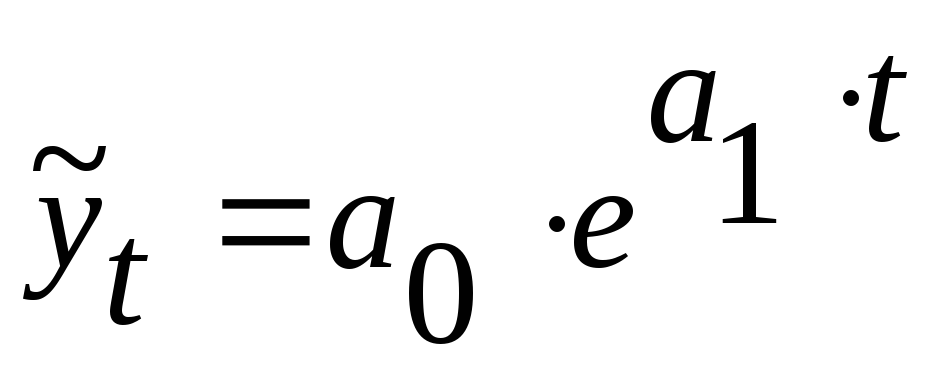Модели сезонной компоненты. Эти модели базируются на использовании гармонического анализа. Так, для полигармонической модели имеем:

Модели случайной компоненты. Опыт пока­зывает, что временной ряд редко удается полностью описать одной лишь детерминированной компонентой. В ней часто присутствует нерегулярная, случайная компонента. Ее поведение нельзя точно предсказать заранее. Для ее описания приходится привлекать понятия из теории вероятностей.

Для описания нерегулярной компоненты и всего временного ряда в це­лом используют понятия случайного (стохастического) процесса илислучайной последовательности как процесса от целочисленного аргумента. Важным классомслучайных процессов являютсянормальные, илигауссовские, случайные процессы.

Простейшей моделью случайной компоненты временного ряда с точки зрения математики является последовательность независимых случайных величин. Среди них наиболее важные – «белый шум» и «гауссовский белый шум».

Белым шумом называется временной ряд (случайный процесс) с ну­левым средним, если составляющие его случайные величины незави­симы и распределены одинаково.

Гауссовский белый шум — это последовательность независимых нормально распределенных случайных величин с нулевым средним и общей дисперсией.